О. А. Заблоцкая

Линейное программирование

ЧАСТЬ 2

Омск 2007

Министерство путей сообщения Российской Федерации

Омский государственный университет путей сообщения

Институт информатики, менеджмента и экономики (ИМЭК)

_________________

О. А. ЗАБЛОЦКАЯ

Линейное программирование

Часть 2

Утверждено редакционно-издательским советом университета в качестве методических указаний по высшей математике для студентов 2-го курса специальностей «Мировая экономика» и «Финансы и кредит»

Омск 2007

УДК 512

Линейное программирование . Часть 2: Методические указания по высшей математике для студентов 2-го курса специальностей «Мировая экономика» и «Финансы и кредит» / О. А. Заблоцкая. Омский гос. ун-т путей сообщения. Омск, 2007. 32 с.

Часть 2 методических указаний посвящена изложению постановок и методов решения транспортной задачи и задачи сетевого планирования.

Для нахождения начального плана перевозок в транспортной задаче предлагается использовать метод северо-западного угла, а дальнейшее улучшение плана до оптимального проводить методом потенциалов. Далее вводится понятие сетевого графика, даются алгоритмы решения задач о кратчайшем сроке и критическом пути, а также приводятся эквивалентные им задачи линейного программирования. Изложение сопровождается примерами решения типовых задач.

Предназначены для студентов 2-го курса специальностей «Мировая экономика» и «Финансы и кредит» очной и заочной форм обучения.

Библиогр.: 11 назв. Табл. 5. Черт. 5.

Рецензент: канд. пед. наук Е. И. Федорова.

_______________________________

 Омский гос. университет путей сообщения, 2007

Содержание

1. Математическая модель классической транспортной задачи 5

2. Свойства закрытой транспортной задачи 8

3. Метод северо-западного угла 9

4. Двойственная транспортная задача и ее экономическая интерпретация 10

5. Метод потенциалов 11

6. Некоторые определения из теории графов 15

7. Понятие сетевого графика 17

8. Задача о кратчайшем сроке 19

9. Задача о критическом пути 21

10. Задачи ЛП, эквивалентные задачам о критическом пути и кратчайшем сроке 25

Библиографический список 26

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КЛАССИЧЕСКОЙ ТРАНСПОРТНОЙ ЗАДАЧИ

Имеется m пунктов производства («поставщиков») и n пунктов потребления («потребителей») некоторого однородного продукта. Требуется организовать снабжение потребителей из пунктов производства так, чтобы суммарные транспортные издержки были минимальными. Предполагается, что могут быть организованы перевозки от любого поставщика любому потребителю, а транспортные издержки пропорциональны объему перевозки.

Для каждого пункта производства ,, и для каждого пункта потребления, заданы следующие величины:

объем производства (запасы) в пункте ,;

объем потребления (спрос) в пункте ;

стоимость перевозки единицы продукта от i-го поставщика j-му потребителю (транспортные затраты).

Требуется найти такой план перевозок, который позволит:

1. не превысить возможности поставщиков;

2. удовлетворить спрос всех потребителей;

3. минимизировать суммарные транспортные затраты.

Построим математическую модель сформулированной транспортной задачи (ТЗ). Для этого введем переменные , представляющие собой объемы перевозок от каждого поставщикакаждому потребителю,,. Матрица

называется планом перевозок.

Составим задачу линейного программирования, являющуюся математической моделью ТЗ:

(1)

Очевидно, что в случае разрешимости задачи (1) выполняется следующее неравенство:

,

т. е. общий объем производства покрывает суммарный спрос. Таким образом, мы получили

Необходимое условие разрешимости ТЗ. Если ТЗ (1) имеет решение, то выполняется неравенство:

. (2)

В случае строгого неравенства в формуле (2) ТЗ называется открытой. Если же выполнено условие баланса

, (3)

то ТЗ называется закрытой и имеет следующий вид:

(4)

Заметим, что любая открытая ТЗ может быть сведена к закрытой путем введения фиктивного (n+1)-го потребителя с потребностью

и транспортными затратами ,i= 1, …, m.

Пример 1. Две базы, на которых собираются излишки картофеля в данном районе, снабжают три города: 1, 2 и 3. Суточная потребность городов в картофеле составляет соответственно 500, 400 и 400 т. Базы могут доставить соответственно 500 и 800 т картофеля. Расходы на перевозку 1 т картофеля до каждого из городов приведены в табл. 1. Требуется составить план перевозок картофеля, минимизирующий суммарные транспортные затраты.

Т а б л и ц а 1

Базы	Города			Запасы
	1	2	3
1	8	5	5	500
2	4	6	8	800
Потребности	500	400	400

Составим математическую модель этой задачи. Очевидно, что суммарные потребности совпадают с общим объемом запасов, т. е. выполнено условие баланса (500+400+400=500+800). Это значит, что транспортная задача является закрытой.

(5)

Заметим, что ТЗ является частным случаем задачи линейного программирования и может быть решена методами линейного программирования. Однако имеются более простые методы, учитывающие специфику ТЗ. В дальнейшем рассмотрим один из них метод потенциалов.

2. СВОЙСТВА ЗАКРЫТОЙ ТРАНСПОРТНОЙ ЗАДАЧИ

Свойство 1. Множество допустимых решенийDзадачи (4) не пусто тогда и только тогда, когда выполняется условие баланса (3).

Доказательство.1) Пусть задача (4) имеет некоторое допустимое решениеxD.Тогда

.

Следовательно, условие баланса (3) выполнено.

2) Пусть выполнено условие (3), т. е. .

Найдем какое-либо допустимое решение задачи (4) xD. Положим

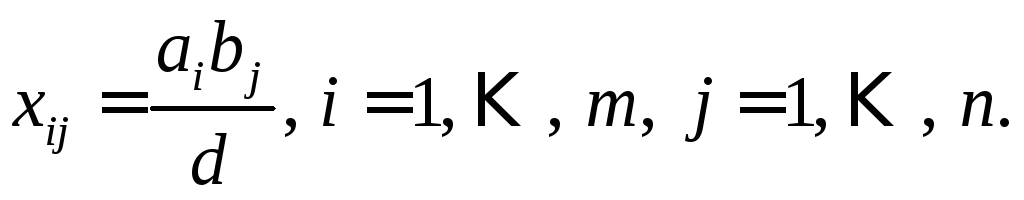
Тогда Следовательно, ограничения задачи (4) выполнены иxD. Что и требовалось доказать.

Свойство 2. В случае целочисленности, (;) оптимальный план перевозокХ также имеет все целочисленные элементы.

Справедливость этого свойства будет вытекать из алгоритма решения закрытой ТЗ.

План перевозок будем изображать в виде таблицы

Х=

	…
…	…	…
	…

Определение 1.Маршрутомв таблицеХназывается такая последовательность клеток, в которой клетканаходится в одной строке таблицы с одной из клетоки в одном столбцес другой,i= 2, …,p1.

Определение 2. Маршрут называется циклом, если клеткиисовпадают.

Определение 3. План называетсяациклическим, если из клеток таблицыХ, соответствующих ненулевым значениям, нельзя составить цикл.

Напомним, что допустимое решение задачи ЛП (4) называется опорным, если система вектор-столбцов матрицы ограничений, соответствующая ненулевым компонентам решения, является линейно независимой.

Свойство 3. План перевозок является опорным тогда и только тогда, когда он ациклический.

Далее рассмотрим один из методов нахождения начального опорного плана ТЗ.

3. МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА

Дана закрытая ТЗ (4). Рассмотрим «северо-западный» угол незаполненной таблицы Х, т. е. клетку (1, 1). Полагаем:

.

Если , то. Это означает, что первый поставщик отгрузил весь имеющийся у него продукт первому потребителю и «выбыл из игры», т. е. полагаем. При этом неудовлетворенный спрос в первом пункте потребления.

Если , то, т. е. спрос первого потребителя полностью удовлетворен, и теперь он «выбывает из игры». Поэтому, а остаток продукта в первом пункте производства.

Если , то из рассмотрения можно исключить и поставщика, и потребителя. Однако условимся считать, что выбывает только поставщик, а неудовлетворенный спрос потребителя равен нулю.

После этого рассматриваем северо-западный угол оставшейся незаполненной части таблицы Хи повторяем те же действия. Продолжая этот процесс, очевидно, через (m+n1) шаг получим ациклический, т. е. опорный план перевозок.

Пример 2. Найдем начальный опорный план ЗТЗ из примера 1.

Х=

500	0	0	500	0	0	0
0	400	400	800	800	400	0
500	400	400
0	400	400
0	0	400
0	0	0

В таблице Х(размера 23) указаны объемы перевозок, полученные методом северо-западного угла. В «пристройках» к таблице справа и внизу содержатся последовательно меняющиеся объемы возможных поставок и потребностей. В таблицеХшрифтом выделены перевозки, соответствующие северо-западным клеткам. В число отмеченных вошла фиктивная перевозка, так как на первом шаге метода мы имелии исключили из рассмотрения только первого поставщика, считая неудовлетворенный спрос первого потребителя. Смысл такого включения фиктивных клеток в опорный план станет ясен позже.

4. ДВОЙСТВЕННАЯ ТРАНСПОРТНАЯ ЗАДАЧА И ЕЕ ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

Для простоты записи рассмотрим закрытую ТЗ с двумя поставщиками и тремя потребителями. Умножим равенства, соответствующие поставщикам, на 1 и составим двойственную задачу.

( )

( )

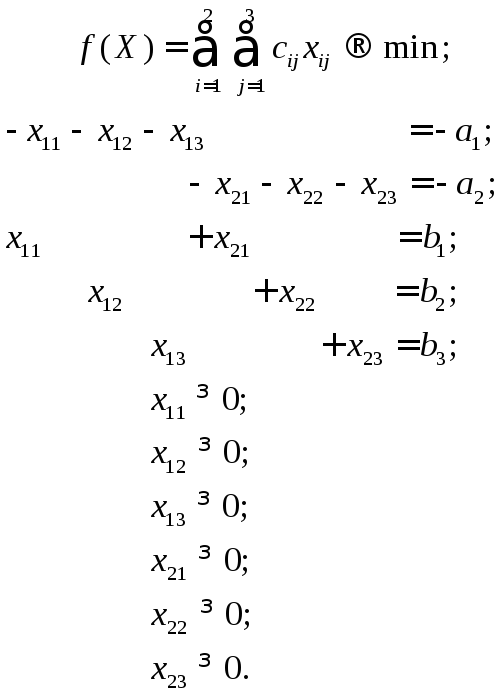
Переменные называютсяпотенциалами пунктов производства и потребления соответственно. Их можно трактовать как условные цены продукта до и после транспортировки. Но реальный смысл имеет разность потенциалов, т. е. возрастание стоимости продукта при перевозке. Поэтому сами переменныемогут быть равны нулю и даже отрицательны.

Из теорем двойственности вытекают следующие утверждения.

Теорема 1. При оптимальном плане перевозоксуммарные транспортные затраты равны приращению суммарной оценки стоимости перевозимого продукта:

Теорема 2 (критерий оптимальности). План перевозокоптимален тогда и только тогда, когда существуют такие потенциалы, для которых:

1)

2) при

Таким образом, при оптимальном плане приращение стоимости продукта при перевозке его из i-го пункта производства вj-й пункт потребления не превосходит затрат на эту перевозку (условие 1). Причем если перевозка в данном направлении осуществляется (), то возрастание стоимости равно транспортным издержкам (условие 2). Отсюда следует, что если, то груз в данном направлении перевозиться не должен (). Это значит, что при оптимальном плане осуществляются лишь рентабельные перевозки.

5. МЕТОД ПОТЕНЦИАЛОВ

Рассмотрим закрытую ТЗ с mпоставщиками иn потребителями. Пустьначальный опорный план, найденный по методу северо-западного угла, причем в таблицу внесена лишь (m+n1) перевозка, соответствующая северо-западным клеткам (среди них могут быть и фиктивные перевозки). Остальные клетки, соответствующие нулевым значениям, оставлены пустыми.

Опишем одну итерацию метода потенциалов.

Шаг 1 (вычисление потенциалов).Обратим в равенства все неравенства двойственной ТЗ, соответствующие ненулевым переменными фиктивным перевозкам, включенным в таблицу. Получим систему (m+n1) уравнения с (m+n) неизвестными следующего вида:

. (6)

Полагая значение одной из переменных, например , равным нулю, находим значения всех остальных неизвестных системы (6). Переходим к шагу 2.

Шаг 2 (проверка на оптимальность).Вычисляем все элементы таблицы оценок:

(7)

Если все , то планоптимальный в силу критерия (теорема 2). Конец. Если же найдется хотя бы одна оценка, то переходим к шагу 3.

Шаг 3 (составление нового плана перевозок).Выберем оценку

.

В таблице пустую клетку, соответствующую переменной, пометим знаком «+» и найдем циклС, содержащий эту клетку и не содержащий других пустых. Все клетки циклаСпометим знаками «+» и «» в порядке чередования. Определим:

.

Составим новый план по правилу:

Перевозка включается в таблицу, а клетка, соответствующая переменной, становится пустой. Таким образом, в таблицезаполнена (m+n1) клетка.

Итерация закончена. На каждой следующей итерации с новым планом повторяются те же действия, что и с планом .

Теоретическим обоснованием метода потенциалов помимо теоремы 2 являются следующие утверждения, доказательство которых предлагается читателю провести самостоятельно.

Теорема 3.Система уравнений (6), дополненная условием, имеет единственное решение.

Теорема 4. Новый план перевозок, полученный на шаге 3, является опорным.

Теорема 5.Еслипоследовательные планы перевозок, полученные методом потенциалов, то.

Пример 3.Решим методом потенциалов закрытую ТЗ (5). Начальный опорный пландля нее был найден в примере 2 методом северо-западного угла.

=

500	0	0
0	400	400

Итерация 1

Шаг 1. Система (6) для планаимеет вид:

Полагая , получим

Шаг 2.Составляем таблицу оценок по формуле (7).

=

0	5	7
0	0	0

Так как , то план не является оптимальным.

Шаг 3.Так какимеет наибольшее значение в таблице, то в таблицепустую клетку, соответствующую переменной, пометим знаком «+». Находим циклС.

=

		
		

.

=

100		400
400	400

Итерация 2

Шаг 1. Система (6) для планаимеет вид:

Полагая , получим

Шаг 2. Составляем таблицу оценок по формуле (7).

=

0	5	0
0	0	7

Так как , то план не является оптимальным.

Шаг 3.В таблицепустую клетку, соответствующую переменной, пометим знаком «+». Находим циклС.

=

	
	

.

=

	100	400
500	300

Итерация 3

Шаг 1.

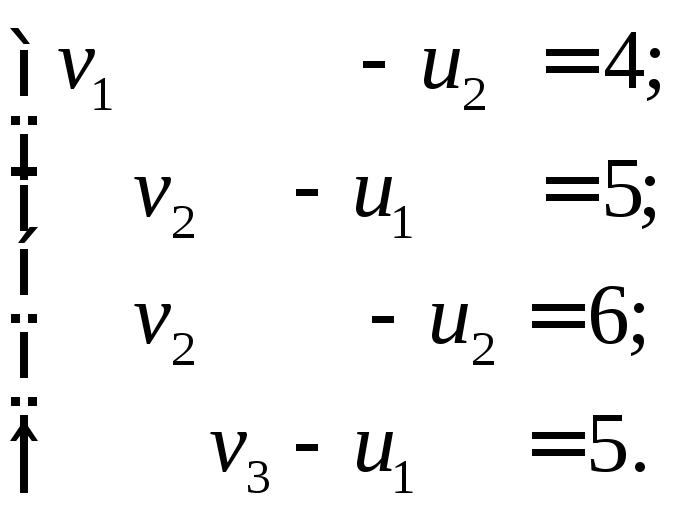
Полагая , получим

Шаг 2.Составляем таблицу оценок по формуле (7).

=

5	0	0
0	0	2

Так как все , то план является оптимальным, а минимальные суммарные транспортные затраты

.

Ответ:оптимальный план перевозок

=

	100	400
500	300

Минимальная стоимость перевозок .

6. НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ ИЗ ТЕОРИИ ГРАФОВ

На практике часто возникают задачи на конфигурациях, состоящих из точек и соединяющих их линий. При этом является несущественным, прямые это линии или же они являются непрерывными кривыми, соединяющими две концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно только то, что они соединяют две данные точки. Примерами могут служить электрическая схема, графическое изображение иерархического строения какой-либо компании или государства, схематическое изображение молекулы некоторого веще- ства и т. п.

Определение 4. Графом G называется математический объект, состоящий из двух множеств: непустого конечного множестваVэлементов, называемыхвершинами, и множестваЕнеупорядоченных и упорядоченных пар вершин. Обозначается графG=(V, E). Неупорядоченная пара вершин называетсяребром, упорядоченная парадугой.

Определение 5. Граф, содержащий только ребра, называетсянеориентированным. Граф, содержащий только дуги,ориентированнымилисетью.

Обычно граф представляют диаграммой на плоскости, изображая его вершины точками, а ребра или дугилиниями, соединяющими соответствующие пары точек. Так, две диаграммы на рис. 1 представляют один и тот же неориентированный граф, имеющий четыре вершины и пять ребер. Ориентированный граф с пятью вершинами и пятью дугами изображен на рис. 2.

Определение 6.Еслиe=(u, v)ребро (дуга) графаG, то вершиныuиv называютсясмежнымииинцидентными ребру (дуге)е.

Ориентированный граф можно задать с помощью таблицы, устанавливающей инцидентность всех его дуг и вершин. Так, изображенная на рис. 2 сеть задается табл. 2.

Т а б л и ц а 2

Номер дуги	1	2	3	4	5
Номера вершин	1, 2	2, 3	2, 4	4, 1	4, 5

Определение 7. Степенью вершиныvназывается число инцидентных ей ребер (дуг). Обозначается степень вершины.

Определение 8. Граф называетсяпростым, если в нем нет петель и кратных ребер, т. е. любая пара вершин инцидентна не более чем одному ребру (дуге) и любое ребро (дуга) соединяет две несовпадающие вершины.

Определение 9.ПодграфомграфаGназывается всякий графс множеством вершини множеством ребер (дуг), каждое из которых инцидентно только вершинам из.

Если не учитывать ориентацию, то все дуги графа становятся его ребрами.

Определение 10. Маршрутомв графеGназывается последовательность ребер, в которой каждые два соседних ребра имеют одну общую вершину. Маршрут называетсяцепью, если в нем все ребра различны, ипростой цепью, если все ее вершины различны.

Определение 11. ГрафGназываетсясвязным, если любая пара его вершин соединена простой цепью. Максимальный связный подграф графаG называетсякомпонентой связностиграфаG. Таким образом, несвязный граф имеет по меньшей мере две компоненты связности.

Определение 12. Путемиз вершиныiв вершинуjориентированного графаGназывается такая последовательность дуг, в которой вершинаi является началом дуги, вершинаj концом дугии конец дугисовпадает с началом дуги,. Количество дугrназываетсядлиной пути. Если начало пути совпадает с его концом (i=j), то путь называетсяконтуром.

Примерами пути в графе, изображенном на рис. 2, являются последовательности дуг ;и др. Лишь один путь представляет собой контур:.

7. ПОНЯТИЕ СЕТЕВОГО ГРАФИКА

Выполнение комплексных исследований, проектирование и строительство крупных объектов и многие другие виды деятельности требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов весьма сложная задача, при решении которой используются так называемые методы сетевого планирования. Рассмотрим следующий пример.

Пример 4. Комплекс работ по строительству здания включает в себя:

а) рытье котлована под фундамент;

б) монтаж фундамента;

в) монтаж подъемного крана;

г) завоз металлоконструкций;

д) монтаж каркаса здания.

По мере выполнения указанных работ наступают следующие события:

1. котлован вырыт;

2. фундамент смонтирован;

3. подъемный кран смонтирован;

4. металлоконструкции завезены;

5. каркас здания смонтирован.

Каждому из этих событий поставим в соответствие вершину графа, а выполняемой при этом работе дугу. Получим ориентированный граф, изображенный на рис. 3. Пунктирной стрелкой на нем изображается фиктивная работа, т. е. работа, не связанная с затратами труда, времени и ресурсов.

Перейдем к построению сетевой модели.

Зависимость между отдельными работами некоторого комплекса зададим с помощью ориентированного графа Г(m, n, S), гдеmколичество вершин,nколичество дуг,ориентированные дуги. Каждую отдельную дугу будем обозначать, она соответствует определенной работе.

Если дуги образуют путь из вершиныв вершину, то это означает, что выполнение работs, для которых, может начаться только после завершения всех работ:. Следовательно, каждую вершину i графаГможно интерпретировать как событие, означающее завершение всех работs, для которых, и возможность начала выполнения всех работs, для которых. Очевидно, что графГне имеет контуров.

Обозначим множества дуг, входящих в вершину i и выходящих из нее,исоответственно. Так как графГне имеет контуров, то в нем найдется вершина, в которую не входит ни одна дуга, и вершина, из которой ни одна дуга не выходит:,=. Будем считать, что=1 и это единственная начальная вершина, а=mединственная конечная вершина. Событиеначало выполнения работ комплекса,завершение всех работ. Понятно, что для любой вершиныi1 в графеГсуществует путь из вершины=1 в вершинуi и для любой вершиныimпуть из этой вершины в вершину=m.Пример графаГ( 8, 14,S) приведен на рис. 4.

Пусть известно время , необходимое для выполнения каждой работы. В этом случае говорят, что имеетсясетевой график , где. Календарный план выполнения сетевого графика определяется вектором, компоненты которого определяют планируемые сроки выполнения соответствующих событий. Планtявляется допустимым, если. При этом время, затраченное на выполнение всего комплекса работ,. Составляя календарный план, мы заинтересованы в минимизации величины.

8. ЗАДАЧА О КРАТЧАЙШЕМ СРОКЕ

Обозначим множество всех допустимых векторовt. Задача о кратчайшем сроке состоит в том, чтобы при заданном сетевом графикенайти такой календарный план, для которого

. (8)

При этом величина называетсякратчайшим сроком.

Обозначим через дляi1 множество всех путей в сети Гиз вершины 1 в вершинуi, а черездляim множество всех путей из вершиныiв вершинуm.

Рассмотрим вектор , имеющий следующие координаты:

; . (9)

Очевидно, что . Следовательно, такой векторявляется решением задачи о кратчайшем сроке. Заметим, что для вычисления координат этого вектора не надо перебирать все пути из множеств, так как соотношения (9) эквивалентны следующим:

; . (10)