
- •О. А. Заблоцкая
- •Содержание
- •Введение
- •Если функции линейные, то задача (1) называется задачей линейного программирования (лп).
- •6. Симплекс-метод
- •7. Нахождение начального базисного решения методом искусственного базиса
- •8. Двойственность в линейном программировании
- •9. Экономическая интерпретация теорем двойственности
- •Библиографический список
- •Линейное программирование Часть 1
- •Типография ОмГупСа
- •644046, Г. Омск, пр. Маркса, 35
О. А. Заблоцкая
Линейное программирование
ЧАСТЬ 1
Омск 2005
Министерство путей сообщения Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
_________________
О. А. Заблоцкая
Линейное программирование
Часть 1
Утверждено редакционно-издательским советом университета в качестве методических указаний по высшей математике для студентов второго курса специальностей «Мировая экономика» и «Финансы и кредит»
Омск 2006
УДК 512 ББК
Линейное программирование. Часть 1: Методические указания по высшей математике / О. А. Заблоцкая; Омский гос. ун-т путей сообщения. Омск, 2006. 45 с.
Методические указания содержат основные теоретические сведения, необходимые для освоения темы «Линейное программирование» в курсе высшей математики. В части 1 приведены различные постановки задачи линейного программирования (ЛП), описан графический метод решения двумерной задачи ЛП, для задачи произвольной размерности изложен симплекс-метод, а также даны понятие двойственной задачи ЛП, основные результаты теории двойственности и их экономическая интерпретация. Изложение теоретического материала сопровождается примерами решения типовых задач. Методические указания содержат также задания контрольной работы по теме «Линейное программирование. Часть 1».
Предназначены для студентов второго курса специальностей «Мировая экономика» и «Финансы и кредит» очной и заочной форм обучения.
Библиогр.: 10 назв. Табл. 11. Рис. 2.
Рецензенты: доктор физ.-мат. наук И.И.Гончар, канд. пед. наук Е. И. Федорова.
_______________________________
Омский гос. университет путей сообщения, 2006
Содержание
Введение 5
Примеры постановок задач 5
Задача линейного программирования 7
Графический метод решения задачи линейного программирования 10
Каноническая задача линейного программирования. Базисные решения 14
Специальная задача линейного программирования 17
Симплекс-метод 19
Нахождение начального базисного решения методом искусственного базиса 24
Двойственность в линейном программировании 28
Экономическая интерпретация теорем двойственности 31
Задачи для самостоятельного решения 32
Библиографический список 44
Введение
В различных областях человеческой деятельности возникают задачи, при решении которых необходим выбор одного из множества вариантов (выбор оптимального плана), например при решении проблем управления и планирования производственных процессов. Математическая дисциплина, разрабатывающая теоретические основы решения подобных задач, называется математическим программированием.
Содержание математического программирования составляют теория и методы решения задач, в математических моделях которых требуется определить экстремум некоторой функции нескольких переменных, связанных условиями в виде равенств и неравенств:
 (1)
(1)
где
![]()
некоторые функции n
переменных.
некоторые функции n
переменных.
Если функции линейные, то задача (1) называется задачей линейного программирования (лп).
Отдельный класс составляют так называемые задачи ЛП транспортного типа и задачи сетевого планирования, для решения которых разработаны методы, учитывающие их специфику. Указанным задачам и методам их решения посвящена часть 2 настоящих методических указаний.
ПРИМЕРЫ ПОСТАНОВОК ЗАДАЧ
Пример 1. Задача о распределении ресурсов
Предприятие
располагает тремя видами ресурсов
![]() ,
необходимыми для производства трех
видов продукции
,
необходимыми для производства трех
видов продукции
![]() .
Затраты ресурсов на производство одной
партии продукции каждого вида, запасы
ресурсов и доход от реализации одной
партии продукции каждого вида приведены
в табл. 1. Определить план выпуска
продукции, позволяющий предприятию
получить максимальный суммарный доход.
.
Затраты ресурсов на производство одной
партии продукции каждого вида, запасы
ресурсов и доход от реализации одной
партии продукции каждого вида приведены
в табл. 1. Определить план выпуска
продукции, позволяющий предприятию
получить максимальный суммарный доход.
Т а б л и ц а 1
|
Ресурс |
Затраты ресурсов на продукцию |
Запас ресурса | ||
|
|
|
| ||
|
|
2 |
4 |
2 |
120 |
|
|
1 |
4 |
3 |
100 |
|
|
3 |
0 |
3 |
200 |
|
Доход |
30 |
50 |
40 |
|
Составим математическую модель этой задачи.
Пусть
![]()
количество выпускаемых партий продукции
количество выпускаемых партий продукции
![]()
![]() .
Вектор
.
Вектор![]() характеризует план выпуска, который
должен удовлетворять следующим
ограничениям, связанным с запасами
ресурсов:
характеризует план выпуска, который
должен удовлетворять следующим
ограничениям, связанным с запасами
ресурсов:
 (2)
(2)
В этих ограничениях имеем неравенства, так как ресурсы могут быть истрачены не полностью.
Суммарный доход от реализации продукции, произведенной в соответствии с планом х, выражается следующей функцией:
![]() .
(3)
.
(3)
Таким образом, получаем следующую задачу математического программирования:
 (4)
(4)
Задача (4) относится к классу задач линейного программирования, так как все фигурирующие в ней функции линейны.
Пример 2. Задача о диете
Рацион солдата складывается из двух продуктов питания, например из хлеба и мяса, питательная ценность которых выражается в количестве протеина и калорий. Их содержание в единице хлеба и мяса, минимальная суточная потребность одного солдата в протеине и калориях, а также стоимость единицы продукта питания приведены в табл. 2. Требуется определить рацион одного солдата, имеющий минимальную стоимость.
Т а б л и ц а 2
|
Продукт питания |
Протеин |
Калории |
Стоимость |
|
Хлеб |
1 |
5 |
1 |
|
Мясо |
5 |
1 |
3 |
|
Потребность |
15 |
15 |
|
Предположим, что
солдат ежедневно получает
![]() единиц хлеба и
единиц хлеба и![]() единиц мяса. Тогда суточные затраты на
питание солдата
единиц мяса. Тогда суточные затраты на
питание солдата
![]() ,
(5)
,
(5)
причем переменные
![]() и
и![]() должны удовлетворять следующим условиям:
должны удовлетворять следующим условиям:
![]() (6)
(6)
Учитывая, что суточные затраты надо минимизировать, получаем следующую задачу линейного программирования:
 (7)
(7)
ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Определение 1. Задачей линейного программирования (ЛП) называется задача математического программирования вида:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() для
некоторых
для
некоторых
![]() . (12)
. (12)
Определение 2. Функция (8) называется целевой.
Определение
3. Любой
вектор
![]() ,
удовлетворяющий условиям (9)−(12),
называетсядопустимым
решением,
или планом
задачи ЛП.
Множество всех планов задачи обозначим
D.
,
удовлетворяющий условиям (9)−(12),
называетсядопустимым
решением,
или планом
задачи ЛП.
Множество всех планов задачи обозначим
D.
Определение
4. Вектор
![]() называетсяоптимальным
решением (оптимальным планом) задачи
ЛП, если
называетсяоптимальным
решением (оптимальным планом) задачи
ЛП, если
![]() для любого
для любого![]() в задаче максимизации или
в задаче максимизации или![]() для любого
для любого![]() в задаче минимизации.
в задаче минимизации.
Определение 5. Задача ЛП (9)−(12) называется разрешимой, если она имеет хотя бы один оптимальный план.
Из
определения задачи ЛП ясно, что она
относится к классу задач на условный
экстремум, однако частные производные
целевой функции
![]() постоянны, т. е. не зависят от точек
постоянны, т. е. не зависят от точек![]() .
Следовательно, обычные методы
математического анализа неприменимы
для решения задач ЛП, поэтому для таких
задач созданы специальные методы,
учитывающие их специфику.
.
Следовательно, обычные методы
математического анализа неприменимы
для решения задач ЛП, поэтому для таких
задач созданы специальные методы,
учитывающие их специфику.
Особый класс задач составляют так называемые канонические задачи.
Определение 6. Канонической задачей ЛП (КЗЛП) называется задача вида:
 (13)
(13)
Заметим, что характерными особенностями КЗЛП являются следующие: целевая функция максимизируется; из ограничений (9)−(11) присутствуют только ограничения, имеющие вид равенств; все переменные задачи неотрицательны.
Определение
7. Две задачи
ЛП называются эквивалентными,
если любому допустимому решению х
одной из них
соответствует допустимое решение
![]() другой и наоборот, причем планх
оптимален
в первой задаче тогда и только тогда,
когда соответствующий ему план
другой и наоборот, причем планх
оптимален
в первой задаче тогда и только тогда,
когда соответствующий ему план
![]() оптимален во второй задаче.
оптимален во второй задаче.
Теорема 1 (теорема об эквивалентности). Для всякой задачи ЛП существует эквивалентная ей каноническая задача ЛП.
Д о к а з а т е л ь с т в о. Для простоты изложения проведем доказательство в случае задачи ЛП, имеющей две переменные и три ограничения (n = 2, m = 3):
 (14)
(14)
Для перехода к эквивалентной КЗЛП необходимо добиться того, чтобы эта задача была на максимум, все линейные ограничения были равенствами и все переменные неотрицательными. Покажем, как этого можно добиться.
1)
Пусть
![]() .
Очевидно, что функция
.
Очевидно, что функция![]() достигает своего максимума тогда и
только тогда, когдаf(x)
достигает
минимума.
достигает своего максимума тогда и
только тогда, когдаf(x)
достигает
минимума.
2)
В линейные ограничения задачи (14),
имеющие вид неравенств, введем
неотрицательные переменные
![]() ,
называемыедополнительными.
Получим следующие ограничения:
,
называемыедополнительными.
Получим следующие ограничения:
 (15)
(15)
3)
По условию задачи (14) переменная
![]() может принимать значения любого знака.
Такую переменную можно представить в
виде разности двух неотрицательных
переменных:
может принимать значения любого знака.
Такую переменную можно представить в
виде разности двух неотрицательных
переменных:
![]()
![]() .
(16)
.
(16)
После выполнения этих преобразований получаем каноническую задачу:
 (17)
(17)
Докажем эквивалентность задач (14) и (17).
Очевидно,
что каждому допустимому решению
![]() задачи (14) соответствует допустимое
решение
задачи (14) соответствует допустимое
решение![]() КЗЛП (17) и наоборот. Действительно, задав
упорядоченную пару
КЗЛП (17) и наоборот. Действительно, задав
упорядоченную пару![]() ,
найдем:
,
найдем:
 (18)
(18)
Для
положительных значений
![]() положим:
положим:![]() ,
для неположительных значений
,
для неположительных значений![]() примем:
примем:![]() .
Тогда для любых значений
.
Тогда для любых значений![]() имеем:
имеем:![]() где
где![]() и
и![]() определяются однозначным образом по
значению
определяются однозначным образом по
значению![]() .
Обратно, задав набор
.
Обратно, задав набор![]() ,
легко получаем упорядоченную пару:
,
легко получаем упорядоченную пару:![]() ,
где
,
где![]() .
.
Оптимальность
или неоптимальность соответствующих
планов задач (14) и (17) следует из соотношения
![]() .
.
Теорема доказана.
Итак, чтобы решить произвольную задачу ЛП, достаточно решить эквивалентную ей каноническую задачу ЛП, и поэтому в дальнейшем можно ограничиться исследованием именно канонических задач ЛП.
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача
ЛП, имеющая только две переменные, может
быть решена графически. В этом случае
допустимое множество D
задачи ЛП (если оно не пусто) образует
на плоскости некоторую область, границами
которой являются прямые линии. Такое
множество назовем многогранным.
Задача ЛП сводится к поиску точки
многогранного множества D,
в которой целевая функция
![]() принимает наибольшее (наименьшее)
значение.
принимает наибольшее (наименьшее)
значение.
Напомним,
что линией
уровня функции
f(x)
называется линия, во всех точках которой
f(x)
принимает
одно и то же значение
![]() ,
т. е. линия, заданная уравнением
,
т. е. линия, заданная уравнением![]() .Градиентом
функции f(x)
называется
вектор
.Градиентом
функции f(x)
называется
вектор
![]() , (19)
, (19)
где
![]()
частные производные функции f(x).
Вектор
частные производные функции f(x).
Вектор
![]() ,
т. е. противоположный вектору
,
т. е. противоположный вектору![]() называетсяантиградиентом.
Если f(x)
линейная функция, то
называетсяантиградиентом.
Если f(x)
линейная функция, то
![]()
постоянный вектор, а линии уровня
прямые линии
постоянный вектор, а линии уровня
прямые линии
![]() перпендикулярные градиенту.
перпендикулярные градиенту.
Из курса высшей математики известно, что градиент указывает направление наискорейшего возрастания функции f(x), а антиградиент убывания, поэтому, чтобы найти наибольшее (наименьшее) значение целевой функции f(x), необходимо мысленно сдвигать линию уровня этой функции в направлении градиента (антиградиента). Точка, в которой линия уровня функции в последний раз касается множества D, будет оптимальной.
З а м е ч а н и я.
1) Если линия уровня целевой функции f(x) касается множества D в последний раз по целому ребру, то задача ЛП имеет бесконечное множество оптимальных решений, они соответствуют каждой точке этого ребра.
2) Если допустимое множество D таково, что сколько бы ни сдвигали линию уровня целевой функции f(x) в направлении градиента для задачи на максимум (антиградиента − для задачи на минимум), она всегда будет пересекать множество D, то функция неограниченно возрастает (убывает) на множестве D. Это означает, что задача ЛП не имеет решения.
Проиллюстрируем графический метод решения задач ЛП на примерах.
Пример 3. Решить задачу ЛП:
 (20)
(20)
И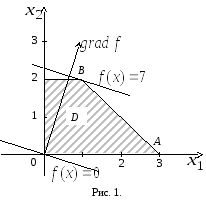 зобразим
на плоскости
зобразим
на плоскости![]() (рис. 1) множествоD
допустимых решений задачи (20). Получим
четырехугольник (заштрихованный).
Градиент целевой функции
(рис. 1) множествоD
допустимых решений задачи (20). Получим
четырехугольник (заштрихованный).
Градиент целевой функции
![]() также изображен на рис. 1.
также изображен на рис. 1.
Через
начало координат проходит линия уровня,
соответствующая уравнению
![]() ,
т. е.
,
т. е.![]() .
Для отыскания наибольшего значения
целевой функции на допустимом множествеD
линию уровня следует мысленно смещать
в направлении вектора
.
Для отыскания наибольшего значения
целевой функции на допустимом множествеD
линию уровня следует мысленно смещать
в направлении вектора
![]() .
При рассмотрении рис. 1 видно, что при
таком перемещении прямой
.
При рассмотрении рис. 1 видно, что при
таком перемещении прямой![]() последнее касание с заштрихованным
четырехугольником произойдет в точкеВ (1;
2), следовательно, оптимальным решением
задачи (20) будет точка
последнее касание с заштрихованным
четырехугольником произойдет в точкеВ (1;
2), следовательно, оптимальным решением
задачи (20) будет точка
![]() .
Подставив ее координаты в целевую
функцию, получим:
.
Подставив ее координаты в целевую
функцию, получим:![]() .
.
Пример 4. Изменим в примере 3 целевую функцию, оставив прежней допустимое множество D. Получим задачу:
 (21)
(21)
Заметим,
что линии уровня функции
![]() имеют уравнения
имеют уравнения![]() ,
т. е. параллельны прямойАВ,
поэтому последнее касание области D
при перемещении линии уровня в направлении
,
т. е. параллельны прямойАВ,
поэтому последнее касание области D
при перемещении линии уровня в направлении
![]() произойдет во всех точках отрезкаАВ.
Следовательно, задача (21) имеет бесконечное
множество оптимальных решений, среди
которых есть две вершины заштрихованного
четырехугольника: А
(3; 0) и
В (1; 2) (см.
рис. 1).
произойдет во всех точках отрезкаАВ.
Следовательно, задача (21) имеет бесконечное
множество оптимальных решений, среди
которых есть две вершины заштрихованного
четырехугольника: А
(3; 0) и
В (1; 2) (см.
рис. 1).
Пример 5. Решим графически задачу о диете (см. пример 2).
Допустимое
множество D
задачи (7),
градиент целевой функции
![]() и ее линия уровня, проходящая через
начало координат и имеющая уравнение
и ее линия уровня, проходящая через
начало координат и имеющая уравнение![]() ,
показаны на рис. 2.
,
показаны на рис. 2.
П оскольку
в задаче требуется найти наименьшее
значение целевой функции на множествеD,
то для его отыскания линии уровня
оскольку
в задаче требуется найти наименьшее
значение целевой функции на множествеD,
то для его отыскания линии уровня
![]() следует перемещать в направлении
антиградиента,
т. е.
следует перемещать в направлении
антиградиента,
т. е.![]() .
Очевидно, что в этом случае последнее
касание линии уровня с областьюD
произойдет в точке
.
Очевидно, что в этом случае последнее
касание линии уровня с областьюD
произойдет в точке
![]() .
Координаты точкиА
можно вычислить, решив систему уравнений
.
Координаты точкиА
можно вычислить, решив систему уравнений
 Следовательно, оптимальное решение
задачи (7)
Следовательно, оптимальное решение
задачи (7)
![]() ,
а оптимальное значение функции
,
а оптимальное значение функции![]() ,
т. е. минимальные суточные затраты на
питание одного солдата составляют 10
денежных единиц.
,
т. е. минимальные суточные затраты на
питание одного солдата составляют 10
денежных единиц.
Заметим,
однако, что если бы в задаче (7) целевую
функцию требовалось максимизировать,
то ее линии уровня следовало бы перемещать
в направлении
![]() ,
и последней точки касания с областьюD
не существовало бы в силу неограниченного
роста функции
,
и последней точки касания с областьюD
не существовало бы в силу неограниченного
роста функции
![]() наD.
В этом случае задача была бы неразрешима.
наD.
В этом случае задача была бы неразрешима.
КАНОНИЧЕСКАЯ ЗАДАЧА ЛП. БАЗИСНЫЕ РЕШЕНИЯ
Рассмотрим
каноническую задачу ЛП (13). Обозначим
через
![]() вектор-столбец, составленный из
коэффициентов при переменной
вектор-столбец, составленный из
коэффициентов при переменной![]() ограничений вида равенств системы (13),
ограничений вида равенств системы (13),![]() ,
а черезB
вектор-столбец свободных членов
,
а черезB
вектор-столбец свободных членов
![]() :
:
 . (22)
. (22)
Тогда задача (13) может быть записана в виде:
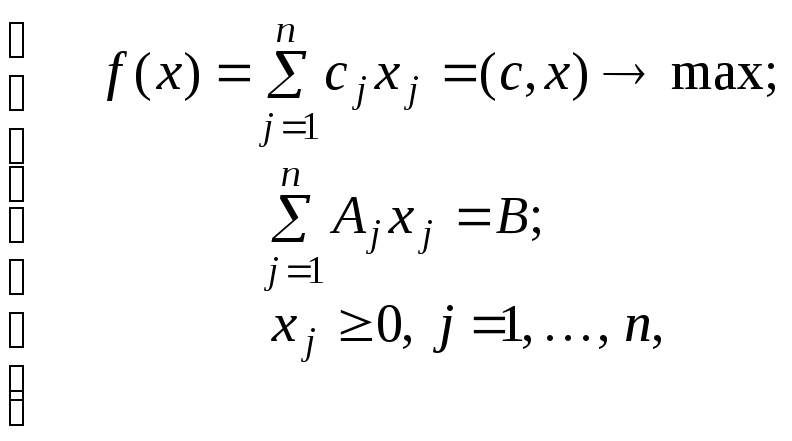 (23)
(23)
где
![]()
скалярное произведение векторов
скалярное произведение векторов
![]() и
и![]() .
.
Определение
8. Допустимое
решение (план)
![]() канонической задачи ЛП (23) называетсябазисным
решением (опорным планом),
если либо
канонической задачи ЛП (23) называетсябазисным
решением (опорным планом),
если либо
![]() ,
либо система вектор-столбцов
,
либо система вектор-столбцов![]() ,
соответствующих ненулевым компонентам
векторах,
линейно независима (напомним, что система
векторов называется линейно
зависимой,
если хотя бы один из векторов системы
является линейной комбинацией остальных,
линейно
независимой
в противном случае).
,
соответствующих ненулевым компонентам
векторах,
линейно независима (напомним, что система
векторов называется линейно
зависимой,
если хотя бы один из векторов системы
является линейной комбинацией остальных,
линейно
независимой
в противном случае).
Пример 6. Рассмотрим каноническую задачу ЛП:
 (24)
(24)
Ее
допустимое решение х
= (0, 0, 1, 2)
является базисным, так как векторы
![]() и
и![]() линейно независимы.
линейно независимы.
Теорема 2 (теорема о существовании оптимального базисного решения). Если каноническая задача ЛП (23) разрешима, то существует ее оптимальное базисное решение.
Д
о к а з а т е л ь с т в о.
Пусть задача
(23) разрешима, т. е. множество ее оптимальных
решений не пусто. Среди всех оптимальных
решений существует такое, которое имеет
наименьшее число ненулевых компонент.
Обозначим его
![]() (если таких решений несколько, то возьмем
за
(если таких решений несколько, то возьмем
за![]() любое из них). Переобозначив при
необходимости переменные
любое из них). Переобозначив при
необходимости переменные![]() можно считать, что
можно считать, что![]() имеет вид:
имеет вид:
![]() (25)
(25)
Докажем,
что
![]() является базисным решением задачи (23).
Предположим, что это не так. Тогда система
векторов
является базисным решением задачи (23).
Предположим, что это не так. Тогда система
векторов![]() ,
соответствующих ненулевым компонентам
вектора
,
соответствующих ненулевым компонентам
вектора![]() ,
линейно зависима: существуют такие не
все равные нулю числа
,
линейно зависима: существуют такие не
все равные нулю числа![]() ,
что
,
что
![]() , (26)
, (26)
где
![]()
вектор-столбец, целиком состоящий из
нулей.
вектор-столбец, целиком состоящий из
нулей.
Введем
n-мерный
вектор
![]() и
рассмотрим скалярное произведение
и
рассмотрим скалярное произведение![]() ,
где
,
где![]()
коэффициенты целевой функции
коэффициенты целевой функции
![]() задачи (23). Без ограничения общности
можно считать, что
задачи (23). Без ограничения общности
можно считать, что![]() (в противном случае вместо вектора
(в противном случае вместо вектора![]() рассмотрим вектор
рассмотрим вектор![]() ).
).
Рассмотрим
вектор
![]() ,
где
,
где .
Если все
.
Если все![]() ,
тоt
произвольное положительное число.
,
тоt
произвольное положительное число.
Проверим,
что вектор
![]() удовлетворяет ограничениям задачи
(23). Действительно, с учетом условия
(26), получим:
удовлетворяет ограничениям задачи
(23). Действительно, с учетом условия
(26), получим:
![]()
![]() (27)
(27)
Неотрицательность
компонент вектора
![]() очевидна, следовательно,
очевидна, следовательно,![]() является допустимым решением задачи
(23).
является допустимым решением задачи
(23).
Кроме
того,
![]() ,
т. е. вектор
,
т. е. вектор![]() имеет меньше ненулевых компонент, чем
вектор
имеет меньше ненулевых компонент, чем
вектор![]() .
.
Вычислим:
![]() .
.
Возможны два случая:
1)![]() .
Тогда
.
Тогда![]() ,
однако это противоречит оптимальности
решения
,
однако это противоречит оптимальности
решения![]() ;
;
2)
![]() .
Можно считать, что вектор
.
Можно считать, что вектор![]() имеет хотя бы одну положительную
компоненту (в противном случае вместо
имеет хотя бы одну положительную
компоненту (в противном случае вместо![]() рассмотрим вектор
рассмотрим вектор![]() ).
Тогда вновь
).
Тогда вновь![]() .
Получим:
.
Получим:
![]() , (28)
, (28)
т.
е.
![]() является оптимальным решением задачи
(23), однако число ненулевых компонент
вектора
является оптимальным решением задачи
(23), однако число ненулевых компонент
вектора![]() меньше, чем у вектора
меньше, чем у вектора![]() ,
а это противоречит определению
,
а это противоречит определению![]() как оптимального решения с наименьшим
числом ненулевых компонент.
как оптимального решения с наименьшим
числом ненулевых компонент.
Полученные
в обоих случаях противоречия доказывают,
что
![]()
базисное решение. Теорема доказана.
базисное решение. Теорема доказана.
Теорема 3 (теорема о конечности множества базисных решений). Если каноническая задача ЛП (23) разрешима, то множество ее базисных решений конечно.
Д
о к а з а т е л ь с т в о. Пусть х
и
![]()
два различных базисных решения задачи
(23). Покажем, что существует такой номер
j,
что j-я
координата одного из векторов х
или
два различных базисных решения задачи
(23). Покажем, что существует такой номер
j,
что j-я
координата одного из векторов х
или
![]() равна нулю, а у другого
отлична от нуля.
равна нулю, а у другого
отлична от нуля.
Действительно,
если предположить противное, т. е., что
все координаты векторов х
и
![]() ,
имеющие одинаковые номера, либо
одновременно равны нулю, либо отличны
от нуля, то можно считать, что
,
имеющие одинаковые номера, либо
одновременно равны нулю, либо отличны
от нуля, то можно считать, что
 , (29)
, (29)
где
![]() ,
но не все
,
но не все![]() равны нулю, так какх
и
равны нулю, так какх
и
![]() предполагаются различными базисными
решениями,
предполагаются различными базисными
решениями,![]() .
.
Рассмотрим:
![]() , (30)
, (30)
так
как х
и
![]()
допустимые решения задачи (23). Следовательно,
система векторов
допустимые решения задачи (23). Следовательно,
система векторов
![]() является линейно зависимой, а это
противоречит тому, чтох
и
является линейно зависимой, а это
противоречит тому, чтох
и
![]()
базисные решения.
базисные решения.
Доказанное
свойство базисных решений позволяет
утверждать, что число базисных решений
разрешимой канонической задачи ЛП (23)
не превосходит числа векторов длины n
с компонентами, равными нулю или единице,
которое, в свою очередь, не больше числа
![]() ,
т. е. конечно. Теорема доказана.
,
т. е. конечно. Теорема доказана.
Из теорем 2 и 3 вытекает, что оптимальное решение канонической задачи ЛП можно искать перебором базисных решений, число которых конечно. Эта идея и лежит в основе излагаемого далее метода последовательного улучшения базисного решения, называемого симплекс-методом.
СПЕЦИАЛЬНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим систему линейных уравнений, входящую в ограничения канонической задачи ЛП (23). Матрицу коэффициентов левых частей уравнений этой системы обозначим А.
Определение 9. Система линейных уравнений называется системой с базисом, если в каждом уравнении имеется переменная, которая входит в это уравнение с коэффициентом 1 и отсутствует в остальных уравнениях. Такие переменные называются базисными, остальные небазисными.
Матрицу А системы с базисом с помощью перенумерации переменных можно привести к виду:
 . (31)
. (31)
Определение 10. Каноническая задача ЛП (23) называется специальной, если
ее система линейных уравнений является системой с базисом;
правые части уравнений системы неотрицательны:

 ;
;целевая функция
 выражена только через небазисные
переменные.
выражена только через небазисные
переменные.
Специальная задача ЛП имеет вид:
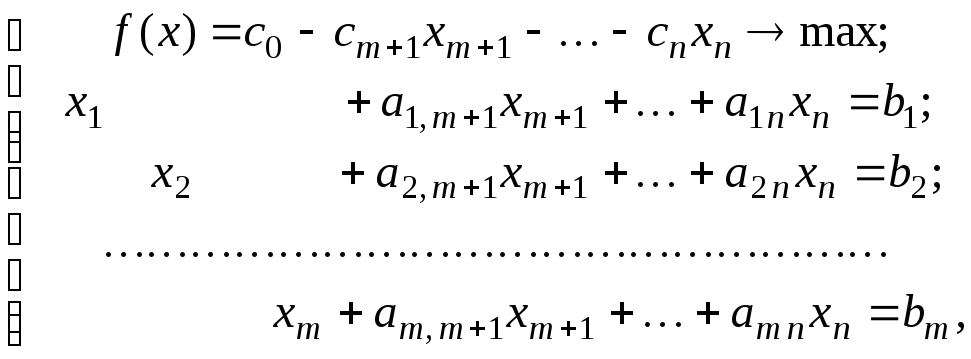 (32)
(32)
где
![]()
базисные,
базисные,
![]()
небазисные переменные,
небазисные переменные,
![]() .
.
Пример 7. Привести задачу ЛП к специальному виду:
 (33)
(33)
Вводя
дополнительные переменные
![]() ,
получим каноническую задачу ЛП:
,
получим каноническую задачу ЛП:
 (34)
(34)
В
задаче (34) базисными являются переменные
![]() ,
небазисными
,
небазисными
![]() .
Перенумеруем переменные:
.
Перенумеруем переменные:![]()
![]() .
В результате получим специальную задачу:
.
В результате получим специальную задачу:
 (35)
(35)
