
SAT 8
.pdf
94 |
PART II / MATH REVIEW |
If the scale factor of two similar solids is m:n, then the following ratios are true.
1.The ratio of their corresponding base perimeters or circumferences is also m:n.
2.The ratio of their base areas, total surface areas, and lateral surface areas is m2:n2.
3.The ratio of their volumes is m3:n3.
E X A M P L E :
The lateral surface areas of two similar right cylinders are 80π in3 and 120π in3, respectively. Find the ratio of their volumes.
First determine the scale factor of the similar cylinders by comparing their lateral surface areas.
80π:120π simplifies to 8:12, which simplifies to 2:3. Therefore, the scale factor is 2:3.
Now, find the volume ratio by cubing the scale factor:
23:33.
8:27. (Answer)
*COORDINATES IN THREE DIMENSIONS
Similar to graphing points (x, y) in a two-dimensional xy-coordinate plane, the point (x, y, z) can be graphed in a three-dimensional coordinate system having an x-axis, y-axis and z-axis. For example, the point (2, −3, 1) is a solution to the equation 2x + y − z = 0. The graph of the ordered triple is as shown:
z |
(2,–3,1) |
y |
x |
The distance between ordered triples (x1, y1, z1) and (x2, y2, z2) is given by the formula:
Distance = ( x2 − x1)2 + ( y2 − y1)2 + ( z2 − z1)2 .
CHAPTER 5 / SOLID GEOMETRY |
95 |
E X A M P L E : |
|
What is the distance between (0, 0, 7) and (4, 1, 0)?
The problem is asking for the length of the segment connecting the two points.
Simply apply the distance formula to get:
 (0,0,7)
(0,0,7)
 (4,1,0)
(4,1,0)
d= (4 − 0)2 + (1 − 0)2 + (0 − 7)2 .
d= 42 + 12 + (− 7)2 .
d= 16 + 1 + 49.
d = 66 ≈ 8.12. (Answer)
E X A M P L E :
A right circular cylinder has a height of 10 and a radius of 4. If X and Y are two points on the surface of the cylinder, what is the maximum possible length of XY?
Although this problem doesn’t ask about points specifically in the form (x, y, z), it does ask you to visualize points in three-dimensions. Think of X and Y as vertices of the right triangle shown below.
4 |
x |
|
10
y
8
XY = 82 + 102
XY = 64 + 100
XY = 164 = 2 41 ≈ 12.81 |
(Answer) |
CHAPTER 6
COORDINATE GEOMETRY
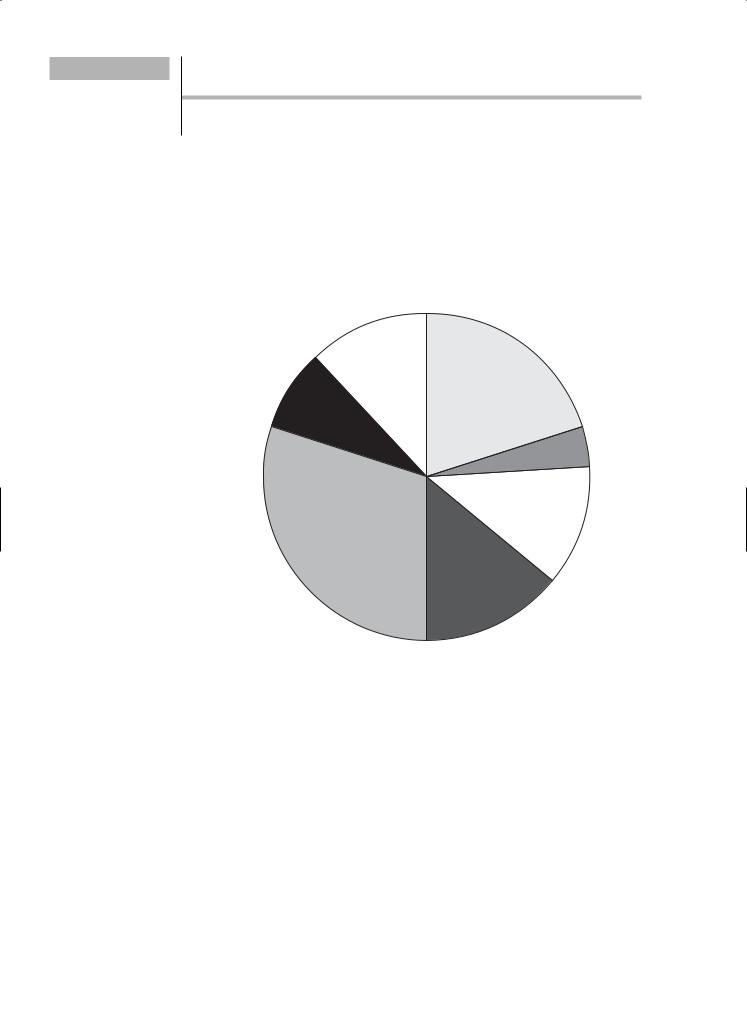
This chapter provides a review of coordinate geometry principles. On the Level 2 test, 10–14% of the questions relate specifically to coordinate geometry. Coordinate geometry focuses on graphing in an xy-coordinate plane. The pie chart shows approximately how much of the Level 2 test is related to coordinate geometry:
Numbers and
Operations
12% Algebra
20%
Data Analysis,
Statistics, and
Probability
8%
Solid
Geometry
4%
Coordinate
Geometry
12%
Functions
30%
Trigonometry
14%
The following geometry topics are covered in this chapter:
1.Plotting Points
2.Midpoint
3.Distance
4.Slope
5.Slope of Parallel and Perpendicular Lines
6.Equations of Lines
a.Horizontal and Vertical Lines
b.Standard Form
c.Point-Slope Form
d.Slope-Intercept Form
e.Determining x and y Intercepts
7.Circles
8.Parabolas
96

CHAPTER 6 / COORDINATE GEOMETRY |
97 |
9.*Ellipses
10.*Hyperbolas
11.Graphing Inequalities
12.Graphing Absolute Value
13.Symmetry
14.Transformations
15.*Polar Coordinates
PLOTTING POINTS
A plane rectangular coordinate system is created by drawing two axes that intersect at right angles at an origin. The horizontal axis is called the x-axis and the vertical axis is called the y-axis. The axes create 4 quadrants in the plane, which are numbered using Roman numerals as shown:
y
II |
I |
 x
x
III IV
An ordered pair (x, y) denotes a unique point in the plane. To plot a point, simply graph the location of its x and y coordinates. The x-coordinate of a point is also referred to as the abscissa, while the y-coordinate is also referred to as the ordinate.
E X A M P L E :
Graph the following points in the same coordinate plane: A(1, 4), B(−2, −3), C(−5, 1), D(4, 0) (see graph on page 98).
*Denotes concepts that are on the Level 2 test only.
98 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PART II |
/ |
MATH REVIEW |
||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
–12 –11 –10 –9 |
–8 |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B –3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
E X A M P L E :
Find three solutions of 2x + 3y = 1.
The graph of an equation in two variables is the set of all points whose x and y coordinates satisfy the equation. To find three solutions to this equation, simply choose 3 values for x and solve for the corresponding value of y. Write y in terms of x, and create an xy-table to determine solutions of the equation.
x |
y = |
|
1 − 2x |
|
y |
|||||
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
y = |
1 |
− 2(0) |
1 |
|
|||||
|
|
|
3 |
|
|
|
3 |
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
y = |
1 |
− 2(2) |
−1 |
||||||
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
y = |
1 |
− 2(−1) |
1 |
|
|||||
|
|
3 |
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

CHAPTER 6 / COORDINATE GEOMETRY |
99 |
|||
The graph of 2x + 3y = 1 is a line, so there are infinitely many points that |
||||
|
will satisfy the equation. Here three possible points are given. |
|||
|
1 |
|
|
|
1, |
|
, (2, −1), (−1, 1) are three possible solutions. |
(Answer) |
|
3 |
||||
|
|
|
||
MIDPOINT
The midpoint of a segment with endpoints (x1, y1) and (x2, y2) is the point:
x1 + x2 |
, |
y1 + y2 |
|
||
|
|
|
|
||
2 |
2 |
||||
|
|
|
|||
Finding the midpoint of a line segment can also be thought of as finding the average of the x and y coordinates.
E X A M P L E :
___
Find the midpoint AB given the endpoints A(1, 6) and B(−3, −7).
Substitute the given coordinates into the midpoint formula to get:
|
1 + −3 |
|
6 + −7 |
||||
|
|
|
|
, |
|
|
. |
2 |
|
2 |
|
||||
|
|
|
|
|
|||
|
−2 |
, |
−1 |
|
|
|
|
|
2 |
|
. |
|
|
||
|
|
2 |
|
|
|
||
|
−1, |
−1 |
|
(Answer) |
|||
|
|
. |
|||||
|
|
2 |
|
|
|
||
E X A M P L E :
___
M is the midpoint of AB . Find the coordinates of B if A has coordinates (3, 8) and M has coordinates (−4, 0).
Let the coordinates of B be (x2, y2), then:
3 + x2 |
= −4 |
and |
8 + y2 |
= 0. |
|
2 |
2 |
||||
|
|
|
|||
3 + x2 = −8 |
|
8 + y2 = 0. |
|||
x2 |
= −11 |
|
y2 = −8. |
||
B(−11,−8). |
(Answer) |
|
|
||
DISTANCE
The distance between any two points (x1, y1) and (x2, y2) is:
d = (x2 − x1 )2 + ( y2 − y1 )2 .
Some aspects of coordinate geometry, simply involve solving a plane geometry question by using an xy-coordinate plane. Here’s an example of one.
100 PART II / MATH REVIEW
E X A M P L E :
Find the perimeter of ABC given its vertices are A(2, 2), B(−1, 5), and C(−5, 2).
This problem requires applying the distance formula three times to find the length of the three sides of the triangle. Solve for AB, BC, and AC
as follows: |
|
|
|
|
|
|
AB = |
(2 − −1)2 + (2 − 5)2 |
= |
(3)2 + (−3)2 |
= |
9 + 9 = |
18 = 3 2. |
BC = |
(−1 − −5)2 + (5 − 2)2 |
= |
(4)2 + (3)2 |
= |
16 + 9 = |
25 = 5. |
AC = |
(2 − −5)2 + (2 − 2)2 |
= |
(7)2 + (0)2 |
= |
49 = 7. |
|
___
Notice that AC is a horizontal line segment, so the distance from A to C can be easily found be determining the change in the x coordinates.2 − −5 = 7. The perimeter of the triangle is:
7 + 5 + 3 |
2. |
12 + 3 2. |
(Answer) |
The concept of distance can also be applied to finding the area of figures in a coordinate plane. Use the distance formula to find the length of the base and/or height of a figure, and substitute these values into the appropriate area formula. (See Chapter 5 for a review of area formulas.)
E X A M P L E :
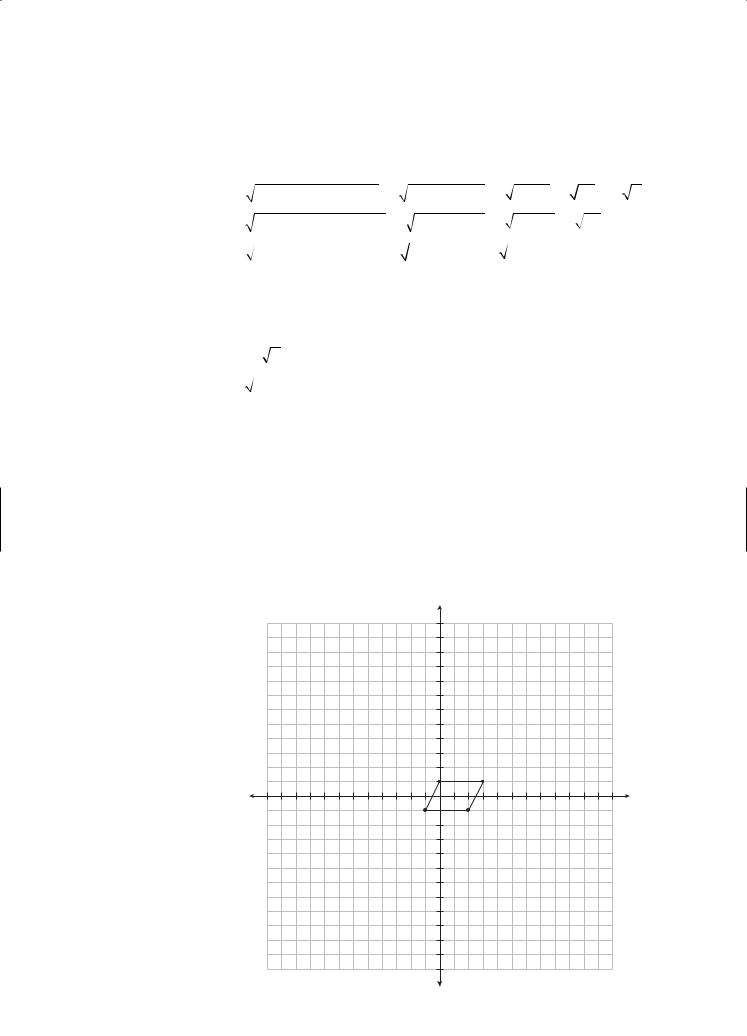
Find the area of parallelogram ABCD given its vertices are A(3, 1), B(2, −1), C(−1, −1), and D(0, 1).
Sketch a diagram to help picture the parallelogram.
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
D |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
x |
–12 –11 –10 –9 |
–8 |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
–1 |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C –2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y
CHAPTER 6 / COORDINATE GEOMETRY |
101 |
___
Assume BC is the base of the parallelogram, and the height is the length of the perpendicular from vertex D to side ___BC. Notice that there is no change in the y-coordinate in the segment BC, so the distance from B to C can be found simply by using absolute value.
BC = 2 − −1 = 3.
The height is 1 − −1 = 2.
The area of the parallelogram is therefore:
A = bh = 3(2) = 6
6 units2. |
(Answer) |
SLOPE
Slope is the measure of the steepness of a line. The slope of a line containing the points (x1, y1) and (x2, y2) is:
slope = |
rise |
= |
change in y |
= |
y2 |
− y1 |
. |
|
|
|
|
||||
|
run |
|
change in x x2 |
− x1 |
|||
Horizontal lines have no change in y, so the slope of a horizontal line is zero.
m = |
0 |
= 0. |
|
change in x
Vertical lines have no change in x. Because you cannot divide by zero, vertical lines have an undefined slope.
= change in y =
m undefined. 0
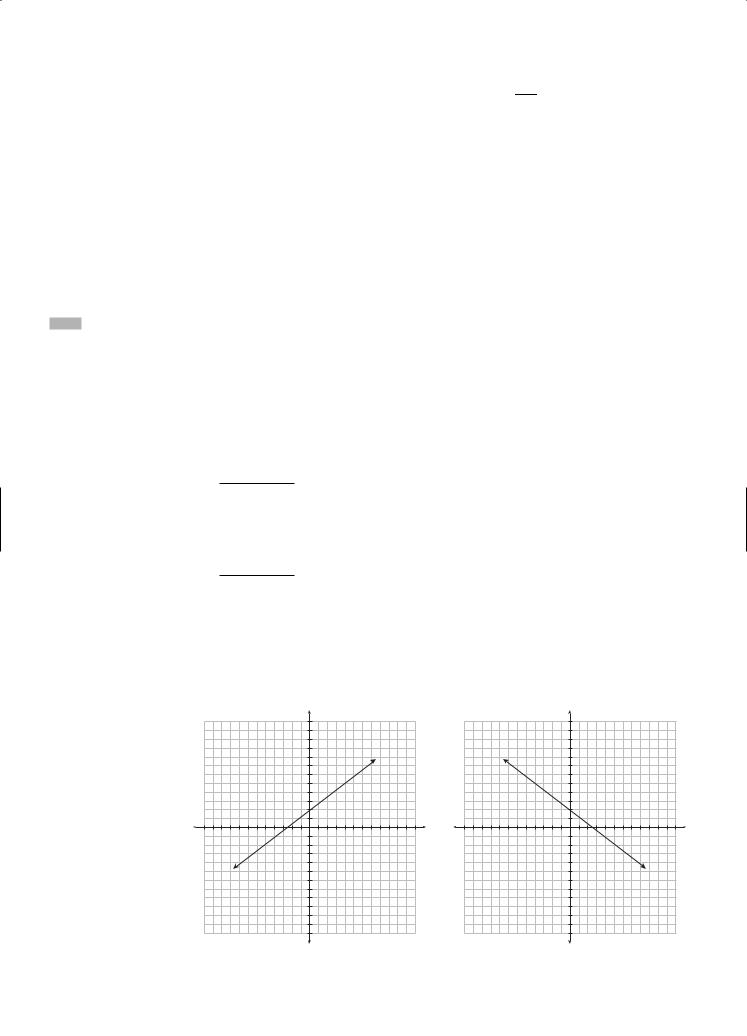
A line having positive slope rises from left to right, and a line having negative slope falls from left to right.
y |
|
y |
|
12 |
|
12 |
|
11 |
|
11 |
|
10 |
|
10 |
|
9 |
|
9 |
|
8 |
|
8 |
|
7 |
|
7 |
|
6 |
|
6 |
|
5 |
|
5 |
|
4 |
|
4 |
|
3 |
|
3 |
|
2 |
|
2 |
|
1 |
|
1 |
|
x –12 –11 –10 –9 –8 –7 –6 –5 –4 –3 –2 –1 0 |
1 2 3 4 5 6 7 8 9 10 11 12 |
x x –12 –11 –10 –9 –8 –7 –6 –5 –4 –3 –2 –1 0 |
1 2 3 4 5 6 7 8 9 10 11 12 x |
–1 |
|
–1 |
|
–2 |
|
–2 |
|
–3 |
|
–3 |
|
–4 |
|
–4 |
|
–5 |
|
–5 |
|
–6 |
|
–6 |
|
–7 |
|
–7 |
|
–8 |
|
–8 |
|
–9 |
|
–9 |
|
–10 |
|
–10 |
|
–11 |
|
–11 |
|
–12 |
|
–12 |
|
y |
|
y |
|
Positive slope |
Negative slope |
||

102 |
PART II / MATH REVIEW |
E X A M P L E :
Find the slope of the line containing the points S(6, −9) and R(−2, −5).
m = y2 − y1 . x2 − x1
m = −5 − −9 . −2 − 6
m = − |
4 . |
|
|
|
8 |
|
|
m = − |
1 |
. |
(Answer) |
|
2 |
|
|
In the above example, we subtracted the coordinates of S from R. Order doesn’t matter, however, as long as you choose the same order in the numerator and the denominator. We could have found the slope by subtracting the coordinates of R from S to get the same answer:
m = |
−9 − −5 |
= − |
4 |
= − |
1 |
. |
|
6 − −2 |
8 |
2 |
|||||
|
|
|
|
SLOPE OF PARALLEL AND PERPENDICULAR LINES
You can determine whether or not lines are parallel (never intersect) or perpendicular (intersect at a right angle) by examining their slope:
1.Parallel lines have the same slope. m1 = m2.
2.Perpendicular lines have slopes that are opposite reciprocals. m1 m2 = −1.
E X A M P L E :
___
Find the slope of the perpendicular bisector of AB given A(0, −2) and
B(3, 3).
___
The slope of AB is:
m = y2 − y1 . x2 − x1
m = 3 − −2 = 5 . 3 − 0 3
___
The slope of any line perpendicular to AB, including the perpendicular
5 bisector, is the opposite reciprocal of 3 .
m = − |
3 . |
(Answer) |
|
5 |
|
EQUATIONS OF LINES
Linear equations are equations whose graphs are straight lines. Equations containing two variables x and y raised to the first power are linear. By definition, linear equations have a constant slope.

CHAPTER 6 / COORDINATE GEOMETRY |
103 |
The following equations are NOT linear: |
|
|||
3x2 + 2y2 = 1 |
3 |
+ 4 y = 5. |
|
|
|
|
|||
|
x |
|
|
|
The following equations are linear: |
|
|||
y = mx + b. |
|
|
y − y1 = m(x − x1 ). |
Ax + By = C. |
Slope-Intercept Form |
Point-Slope Form |
Standard Form |
||
The three forms of the equation of a line are further explained in the succeeding paragraphs.
Horizontal and Vertical Lines
The most basic forms of linear equations are horizontal and vertical lines. Horizontal lines are written in the form y = a, where a is any constant. Vertical lines are written in the form x = a, where, again, a is any constant.
E X A M P L E :
Find the point of intersection of the lines y = 7 and x = 5. The graph of the two lines clearly shows their intersection.
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
–12 –11 –10 –9 |
–8 |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5, 7). (Answer)
Standard Form
The standard form of the equation of a line is:
Ax + By = C (where A and B are both ≠ 0).
The slope of a line in standard form is − BA (B ≠ 0).
