
- •51.1. Понятие системы счисления. Позиционные и непозиционные системы счисления. Методы перевода чисел из одной системы счисления в другую.
- •52.1 Представление чисел с фиксированной и плавающей запятой. Диапазон и точность представления
- •52.2 Типы звеньев данных. Понятие звена данных.
- •52.3 Системы искусственного интеллекта. Методы представлениязнаний. Рассужденияизадачи.
- •53.1 Выполнение операции алгебраического сложения с плавающей запятой
- •53.2 Локальные вычислительные сети. Особенности. Основные распространенные протоколы, методы доступа
- •53.3 Определение базы данных. Уровни представления данных, принцип независимости данных. Схема базы данных
- •54.1 Умножение чисел со старших разрядов в прямом коде
- •Умножение с младших разрядов в дополнительном коде
- •Умножение со старших разрядов в дополнительном коде
- •55.1 Методы выполнения операции деления.
- •2 Деление двоичных чисел с фиксированной запятой
- •2.8. Деление двоичных чисел с плавающей запятой
- •55.2 Язык программирования php. Синтаксис. Основные операторы.
- •56.1 Основные положения и законы алгебры логики
- •56.2 Dhtml. JavaScript. Возможности и области применения
- •2. Моделированиеэкспоненциальнойслучайнойвеличины
- •1. Алгоритм реализации датчика дискретной с.В.
- •2. Пуассоновская с.В
- •58.1.Минимизация логической функции.
- •59.1 Синтез комбинационных логических схем в различных базисах.
- •59.2 Интерфейс программного обмена данными. Структура системной шины.
- •59.3. Реляционная алгебра. Sql
- •60.1.Основные характеристики и параметры интегральных логических элементов. Виды интегральных схем по функциональному назначению.
- •Итнернет технологии
- •2.1 Как работают механизмы поиска
- •60.3 Проектирование реляционной бд, функциональные зависимости, декомпозиция отношений, нормальные формы.
- •62.1 Законы Кирхгофа и преобразование электрических цепей на их основе.
- •63. 1 Электрические источники вторичного питания.
- •Трансформаторный (сетевой) источник питания
- •Габариты трансформатора
- •Достоинства трансформаторных бп
- •Недостатки трансформаторных бп
- •Импульсный источник питания
- •Достоинства импульсных бп
- •Недостатки импульсных бп
- •68.3 Понятие и принципы построения математической модели, параметры и ограничения. Задачи математического программирования, классификация.
- •69.1Аналого-цифровые преобразователи.
- •70.1Цифро-аналоговые преобразователи.
- •70.2 Логические единицы работы многозадачных операционных систем и их использование
- •71.1Источники опорного напряжения и тока.
- •Ион на полевых транзисторах
- •72.3 Общие положения стандарта шифрования данных гост 28147-89 и режим простой замены в стандарте шифрования данных гост 28147-89.
- •73.1 Принципы конвейерной обработки информации в эвм.
- •73.2. Способы адресации и их использование в ассемблерных программах.
- •2. Непосредственная адресация
- •73.3 Понятие политики безопасности: общие положения, аксиомы защищённых систем, понятия доступа и монитора безопасности.
- •1 Человек-пользователь воспринимает объекты и получает информацию о состоянии ас через те субъекты, которыми он управляет и которые отображают информацию.
- •2 Угрозы компонентам ас исходят от субъекта, как активного компонента, изменяющего состояние объектов в ас.
- •3 Субъекты могут влиять друг на друга через изменяемые ими объекты, связанные с другими субъектами, порождая субъекты, представляющие угрозу для безопасности информации или работоспособности системы.
- •74.1Организация памяти эвм. Горизонтальное и вертикальное разбиение. Расслоение обращений. Организация памяти эвм. Горизонтальное и вертикальное разбиение памяти. Расслоение обращений.
- •74.2 Сравнение программных возможностей современных операционных систем ( Windows, Unix).
- •По удобству использования и наличию особых режимов
- •Вопрос 1
- •Вопрос 2
- •Понятие энтропии Энтропия как мера неопределенности
- •Свойства энтропии
- •75.1 Подходы к организации эвм. Эвм, управляемые данными. Эвм, управляемые запросами.
- •Методика построения помехоустойчивых кодов. Информационный предел избыточности
- •1.1. Принципы помехоустойчивого кодирования
- •761 Организация ввода-вывода информации в эвм. Программный обмен, обмен через прерывания, режим прямого доступа к памяти.
- •Организация ввода/вывода информации в эвм. Программный обмен, обмен через прерывания, режим прямого доступа к памяти.
- •Глава II
- •11.1. Проблемы организации систем ввода-вывода
- •11.2. Прямой доступ к памяти
- •9.16. Принципы организации системы прерывания программ.
- •76.2 Динамические структуры данных. Основные виды, способы построения.
- •76.3 Системный анализ, определение и этапы. Сущность системного подхода и его применение при проектировании асоиу.
- •2 Системный анализ. Определение и этапы.
- •77.1 История развития и современное состояние в области микропроцессорных систем.
- •77.2 Стандартные и структурированные типы данных.
- •77.3 Математическое описание объектов управления. Цель и задача управления. Принцип отрицательной обратной связи.
- •2.1. Математические методы построения оптимальных и адаптивных систем управления
- •2.1.1. Математическое описание объектов управления
- •2.1.2. Цель и задача управления
- •2.1.3. Задача оптимального управления и критерии качества
- •78.1 (Он же 80.1) Организация микроЭвм на базе микропрограммируемого микропроцессорного комплекта, типовые циклы функционирования.
- •78.2 Жизненный цикл программных средств. Этапы разработки программного обеспечения.
- •Программное обеспечение
- •Прог. Комплекс Документы
- •78. 3 Критерий качества. Методы решения задач оптимального управления
- •79.2 Нисходящее проектирование алгоритмов на примере моделирования арифметических операций сложения, вычитания, с плавающей запятой.
- •79.3 Понятия управляемости, достижимости и наблюдаемости динамических систем.
- •80.1 Организация микроЭвм на базе микропрограммируемого микропроцессорного комплекта, типовые циклы функционирования.
- •80.2 Восходящий метод проектирования алгоритмов и программ. Спроектировать схему универсального алгоритма перевода чисел из любой системы счисления в любую другую.
- •80.3 Методология структурного проектирования sadt.
2.8. Деление двоичных чисел с плавающей запятой
Деление
чисел, представленных в двоичной форме
с плавающей запятой, выполняется за
четыре шага, при этом условие
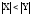 теряет смысл и его проверка не делается.
теряет смысл и его проверка не делается.
1. Определяется знак частного путем сложения по модулю два знаков делимого и делителя.
2. Определяется порядок частного путем вычитания порядка делителя из порядка делимого с учетом их знаков по правилам, аналогичным для вычитания чисел с фиксированной запятой.
3. Определяется мантисса частного путем деления модуля мантиссы делимого на модуль мантиссы делителя по правилам, изложенным выше, для деления чисел с фиксированной запятой.
4. Нормализуется результат деления мантисс делимого и делителя, если произошло переполнение разрядной сетки или денормализация.
5. При переполнении или денормализации мантиссы частного производится соответственно увеличение или уменьшение, вычисленного по п.2, порядка частного.
Пример.
Разделить в двоичной системе с плавающей запятой.
Делимое

Делитель
 .
.
(Под
модуль мантиссы отведено четыре, а под
модуль порядка три разряда). Требуется
найти
 ,
т.е найти
,
т.е найти .
.
Первый шаг. Определение знака частного:
 .
.
Второй шаг. Определение порядка частного путем вычитания порядка делителя из порядка делимого с учетом их знаков в дополнительном модифицированном коде:

+
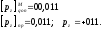
Третий шаг. Определение модуля мантиссы частного (операция выполняется в модифицированном дополнительном коде):

+

+

+
 .
.
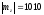
Произошло
переполнение разрядной сетки и требуется
нормализация вправо мантиссы частного,
т.е. сдвиг мантиссы
 на один разряд вправо и увеличение
порядка
на один разряд вправо и увеличение
порядка на единицу.
на единицу.
Четвертый шаг. Нормализация мантиссы частного путем сдвига ее на один разряд вправо:
 .
.
Пятый шаг. Увеличение предварительно полученного порядка частного на единицу в модифицированном дополнительном коде:

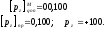
Операция деления двух двоичных чисел с плавающей запятой завершена.

Пример.
Разделить в двоичной системе с плавающей запятой, отведя под мантиссу шесть, а под порядок три разряда.
Делимое

Делитель

Требуется
найти
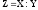 ,
т.е. найти
,
т.е. найти .
.
После нормализации операндов имеем:

Первый шаг. Определение знака частного:

Второй шаг. Определение порядка частного путем вычитания порядка делителя из порядка делимого с учетом их знаков в дополнительном модифицированном коде:


Третий шаг. Определение модуля мантиссы частного (операция выполняется в модифицированном дополнительном коде). При этом, чтобы получить шесть верных разрядов мантиссы частного, увеличим длину разрядной сетки, отводимую для выполнения операции деления мантисс, до восьми разрядов:

11,11000000 < 0; (Это означает, что модуль мантиссы делимого
+
 00,01100000 меньше
модуля мантиссы делителя)
00,01100000 меньше
модуля мантиссы делителя)

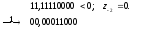
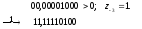
+
+
+
+
+
+



На
этом процесс деления модулей мантисс
заканчиваем, т.к. поставленное выше
условие выполнено – получено шесть
верных разрядов модуля мантиссы частного
 .
.
В связи с тем, что переполнение разрядной сетки и денормализация мантиссы частного отсутствуют, получаем окончательный результат деления в следующем виде:

 .
.
Десятичные числа:
Деление десятичных чисел в ЭВМ
Деление представляет многошаговый процесс. Для определения цифр частного необходимо произвести последовательное вычитание делителя из делимого, при этом если очередной остаток положительный или равен нулю, то в соответствующий разряд частного добавляется единица. Деление можно производить с восстановлением и без восстановления остатка.
При делении без восстановления остатка в том случае, когда образуется отрицательный остаток, делитель сдвигают на один десятичный разряд вправо по отношению к остатку и продолжают деление, прибавляя делитель к отрицательному остатку с приписанным справа следующим разрядом делимого. После первого такого прибавления в очередном разряде частного устанавливается цифра 9. На каждом очередном этапе сложения содержимое этого разряда частного уменьшается на единицу. При новом появлении положительного остатка в данном разряде зафиксируется искомая цифра разряда частного. Далее осуществляется переход к определению следующей цифры частного.
Если делимое не делится нацело, то для целей округления можно определить дополнительную цифру частного.
Пример.
Вычислить
десятичное частное
 при
при по методу с восстановлением остатка.
по методу с восстановлением остатка.
Для простоты и наглядности операции будем производить вначале деление в десятичной системе счисления.
Сумматор Частное

Делимое
 0 5 6
0 5 6
 доп.
= 920 + 9 2 0
доп.
= 920 + 9 2 0
Восстановление 9 7 0 0 (остаток меньше 0)
остатка
 пр.
= 080 + 0 8 0
пр.
= 080 + 0 8 0
0 5 6
1
Сдвиг
делителя
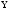 9 9 2
9 9 2
 доп.
= 992 0 4 8 01 (остаток больше 0)
доп.
= 992 0 4 8 01 (остаток больше 0)
+
9 9 2
0 4 0 02 (остаток больше 0)
+
9 9 2
0 3 2 03 (остаток больше 0)
+
9 9 2
0 2 4 04 (остаток больше 0)
+
9 9 2
0 1 6 05 (остаток больше 0)
+
9 9 2
0 0 8 06 (остаток больше 0)
+
9 9 2
0 0 0 07 (остаток равен 0)
Таким образом, Z=X :Y= 7.
