14.Дин. сист. с 1 ст. своб
.docЛекция 14
Системы с одной степенью свободы
-
Математическая модель
Податливость определяется аналитически или численно. Ее определение не представляет проблемы да же в сложных конструкциях. Так как есть множество расчетных пакетов для статики. Мера инерции – масса или момент инерции массы также легко определяется расчетом или экспериментально (см. теоретическую механику). Для многих типовых конструкций перемещения (т.е. податливости) приводятся в справочниках.
Рассмотрим еще один характерный пример – вал с массивным диском массой m и моментом инерции массы Jm по средине. Массой вала пренебрегаем.
С
R
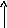 истема
имеет две независимые степени свободы
– вертикальное перемещение и поворот
в плоскости. Их независимость определяется
тем, что ввиду симметрии задачи поворот
не вызывает перемещения и наоборот. В
первом случае мера инерции m,
а податливость
истема
имеет две независимые степени свободы
– вертикальное перемещение и поворот
в плоскости. Их независимость определяется
тем, что ввиду симметрии задачи поворот
не вызывает перемещения и наоборот. В
первом случае мера инерции m,
а податливость
![]() .
Во втором случае
.
Во втором случае
м ера
инерции
ера
инерции
![]() ,
а податливость
,
а податливость
![]() .
Значения податливостей легко определяются
аналитически. Оставим это упражнение
по расчету поперечного изгиба на
подготовку к экзамену.
.
Значения податливостей легко определяются
аналитически. Оставим это упражнение
по расчету поперечного изгиба на
подготовку к экзамену.
Заметим , что малейшая несимметрия в этой задаче приводит в системе с двумя степенями свободы.
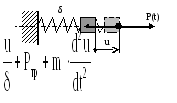 В
дальнейшем изложении для сокращения
записей меру инерции будем обозначать
m,
а внешние нагрузки считать силами.
Среди действующих сил выделим кроме
внешних воздействий P(t)
(силовое возбуждение) внутренние: от
упругого элемента (u/δ),
силы трения (Ртр
) (сопротивления
движению), силу инерции
В
дальнейшем изложении для сокращения
записей меру инерции будем обозначать
m,
а внешние нагрузки считать силами.
Среди действующих сил выделим кроме
внешних воздействий P(t)
(силовое возбуждение) внутренние: от
упругого элемента (u/δ),
силы трения (Ртр
) (сопротивления
движению), силу инерции
![]() и
сформулируем условие равновесия
инерционного элемента
и
сформулируем условие равновесия
инерционного элемента
![]() .
.
После преобразования
![]()
![]() . (*)
. (*)
В формуле обозначено
![]() .
Модель
замыкается начальными условиями:
.
Модель
замыкается начальными условиями:
![]() .
.
Вид уравнения (*) и его решения существенно зависят от Ртр.
Сила трения в общем случае определяется свойствами среды и параметрами движения. При незначительном трении, величиной которого можно пренебречь, и при трении, пропорциональном скорости, уравнение (*) линейно и имеет аналитическое решение. Во всех остальных случаях (сухое трение, трение, зависящее от степени скорости и ускорения, и др.) возможно только численное решение. Решение всегда приближенно, так как модель не полностью соответствует объекту. Важно правильно оценивать степень приближенности при не учете некоторых факторов, что будет сделано ниже.
-
Решение без учета трения
Основное уравнение принимает вид
![]() , (**)
, (**)
линейно; решение
состоит из общего решения однородного
уравнения
![]() и частного решения уравнения с правой
частью
и частного решения уравнения с правой
частью
![]() ,
т.е.
,
т.е.
![]()
При этом, решая методом Эйлера, получаем
![]() ,
,
а частное решение ищем в виде правой части или методом вариации произвольных постоянных.
Рассмотрим основные задачи динамики для этого случая.
1.Очевидно, что
![]() - круговая частота собственных колебаний
и равна
- круговая частота собственных колебаний
и равна
![]()
и мы решили первую основную задачу.
2. Динамический коэффициент при ударе получим в двух вариантах.
Первый – удар с
известной скоростью V
при P(t)=0.
В этом случае u2
=0, начальные условия: u(0)=0,
![]() ,
откуда B=0,
,
откуда B=0,
![]() и
и
![]() .
.
Сила удара
![]() ,
а коэффициент динамичности
,
а коэффициент динамичности
![]() .
.
Здесь обозначено
![]() -
статическое перемещение, т.е. перемещение
от статического приложения веса
ударяющего груза.
-
статическое перемещение, т.е. перемещение
от статического приложения веса
ударяющего груза.
Второй – удар
груза, падающего с высоты H.
При этом скорость при ударе
![]() ,
,
![]() ,
,
![]() и решение
и решение
![]() .
.
С учетом граничных
условий
![]() ,
,
![]()
![]() и
и
![]() .
.
Откуда
![]() ,
,
![]() .
.
Решена вторая основная задача.
3. Исследуем АЧХ при периодическом возмущении от вибрации основания (кинематическое возбуждение). Уравнение равновесия
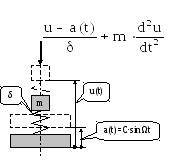
![]()
приводит к дифференциальному уравнению
![]() .
.
Частное решение в виде правой части
![]()
определяет вынужденные колебания. Коэффициент динамичности – отношение амплитуды вынужденных колебаний основания
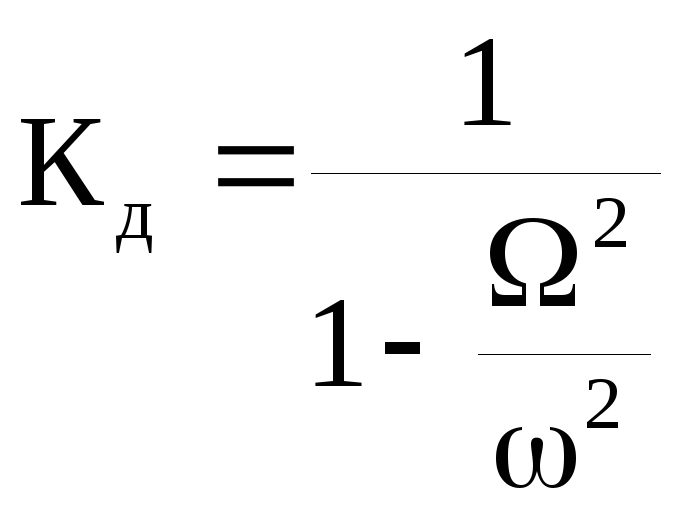
 ,
а его зависимость от отношения
,
а его зависимость от отношения
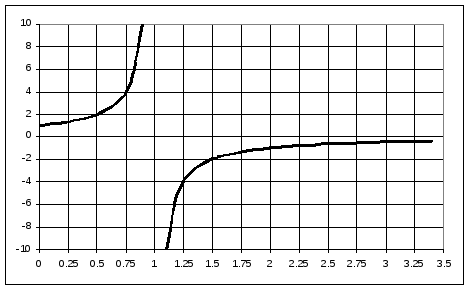
![]() и есть АЧХ. Защита от
вибраций наступает при
и есть АЧХ. Защита от
вибраций наступает при
![]() когда [Кд
] ≤
1. До этого вибрации больше возбуждения
и возможен резонанс.
когда [Кд
] ≤
1. До этого вибрации больше возбуждения
и возможен резонанс.
Резонанс наступает не мгновенно. Рассмотрим процесс подробнее.
![]() .
.
При нулевых
начальных условиях
![]() после преобразований
после преобразований
![]()
![]() .
.
При
![]() получаем
неопределенность типа 0/0. Раскрывая по
правилу Лопиталя, имеем
получаем
неопределенность типа 0/0. Раскрывая по
правилу Лопиталя, имеем
![]()
Период вынужденных колебаний
![]() ,
,
и окончательно получаем при резонансе
![]() .
.
Г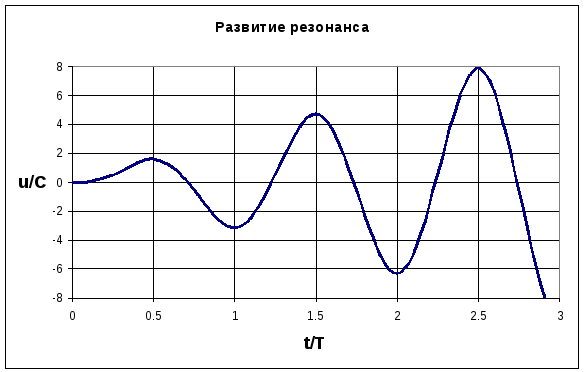 рафик
развития резонанса представлен на
рисунке. Если резонанс длится не более
Т/2, то Кд<
рафик
развития резонанса представлен на
рисунке. Если резонанс длится не более
Т/2, то Кд<![]() ,
при
,
при
![]() и т.д. Таким образом, виброзащита
в одномассовой системе достигается при
и т.д. Таким образом, виброзащита
в одномассовой системе достигается при
![]() и быстром разгоне до таких частот при
запуске.
и быстром разгоне до таких частот при
запуске.
Решена третья задача динамики.
-
Решение при трении, пропорциональном скорости
Рассматривается
случай Ртр
=к·![]() .
Обозначив
.
Обозначив
![]() , из (*) получаем
, из (*) получаем
![]()
![]() , (***)
, (***)
Общее решение
однородного уравнения ищем подстановкой
Эйлера
![]() ,
что приводит к характеристическому
уравнению для
,
что приводит к характеристическому
уравнению для
![]()
![]() ,
,
решение которого
![]()
зависит от
соотношения n
и
![]() :
колебательное при
:
колебательное при
![]() и
и
![]() ,
где
,
где
![]() ,
,
и апериодическое
при
![]() и
и
![]() .
Реально трение относительно невелико
и практически реализуется колебательное
решение, согласно которого
.
Реально трение относительно невелико
и практически реализуется колебательное
решение, согласно которого
![]() .
.
Рассмотрим основные задачи динамики и сравним результаты с задачей без учета трения.
-
Круговая частота собственных колебаний
![]() ,
,
где коэффициент
демпфирования
![]() в
естественных условиях не превышает 0,3
и только в специальных устройствах
(амортизаторы, устройство гашения
колебаний в стрелочных гальванометрах
и.т.п.) достигает 0,5. Поэтому, решение с
учетом трения мало отличается от решения
без учета трения.
в
естественных условиях не превышает 0,3
и только в специальных устройствах
(амортизаторы, устройство гашения
колебаний в стрелочных гальванометрах
и.т.п.) достигает 0,5. Поэтому, решение с
учетом трения мало отличается от решения
без учета трения.
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
1,005 |
1,02 |
1,05 |
1,08 |
1.15 |
Таким образом, решение без учета трения практически точно, так как погрешность лежит в пределах точности вычислений в сопротивлении материалов.
2. Учтем затухание колебаний при динамических воздействиях.
Коэффициент затухания за период колебаний
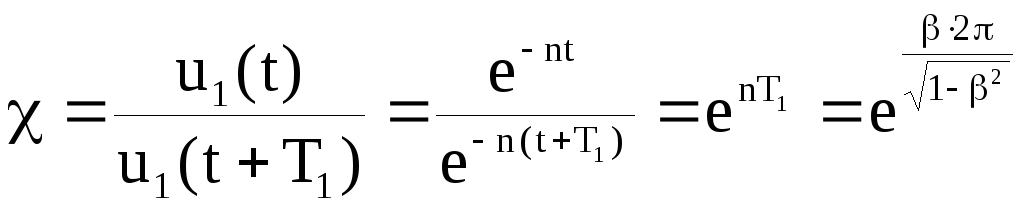 .
.
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
1,94 |
4,08 |
9,52 |
25,65 |
85,02 |
Как видно из таблицы, собственные колебания быстро затухают и практически могут не учитываться при длительном динамическом процессе.
При ударе, который длится одну четвертую периода,
![]()
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
1,18 |
1,42 |
1,75 |
2,25 |
3,04 |
Ударные нагрузки без учета сопротивления рассчитываются с запасом до 1,75.
-
АЧХ с учетом трения, конечно, не уходит в бесконечность при резонансе.
При кинематическом возбуждении
![]() . ****)
. ****)
Ищем частное решение в виде
![]() .
.
После подстановки в (****) и приравнивания коэффициентов при синусе и косинусе, получаем систему
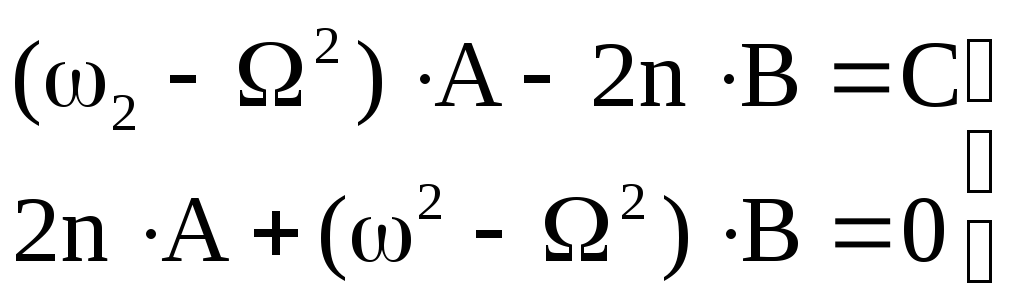 ,
,
решение которой
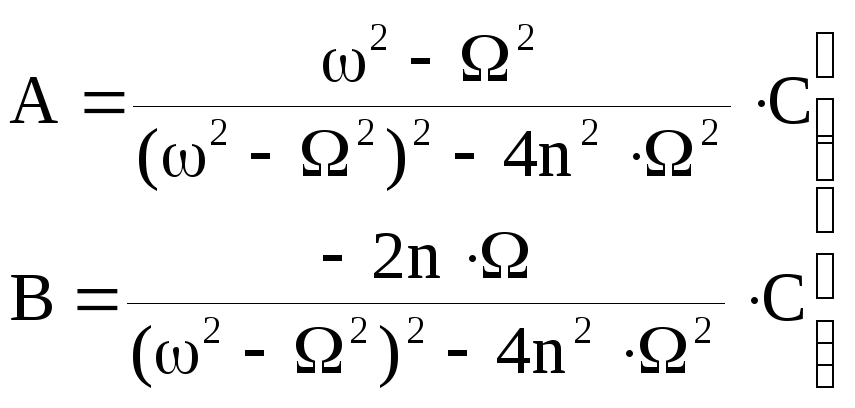 ,
,
позволяет найти
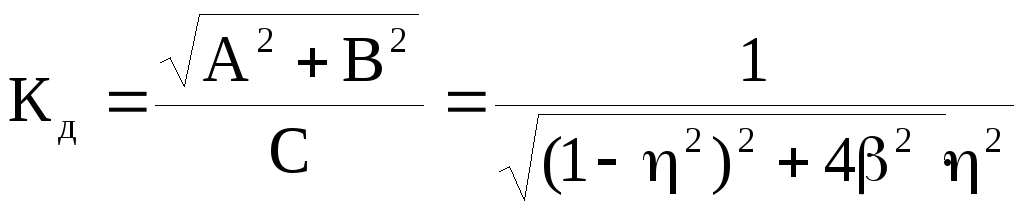 .
АЧХ при разных значениях
.
АЧХ при разных значениях
![]() представлены
на рисунке. Защита от вибраций наступает:
представлены
на рисунке. Защита от вибраций наступает:
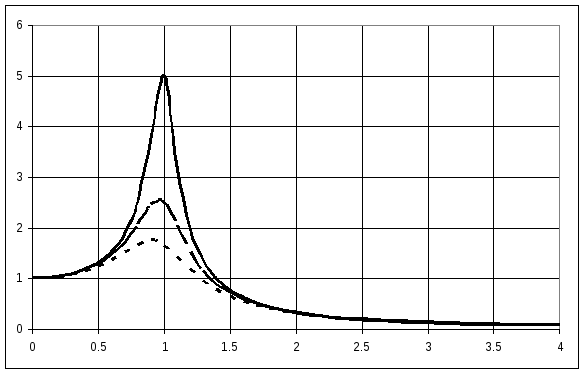
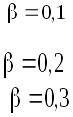
при
![]() если
если
![]() ,
при
,
при
![]() если
если
![]() ,
при
,
при
![]() если
если
![]() .
.
и менее быстром разгоне при запуске, чем без трения.
-
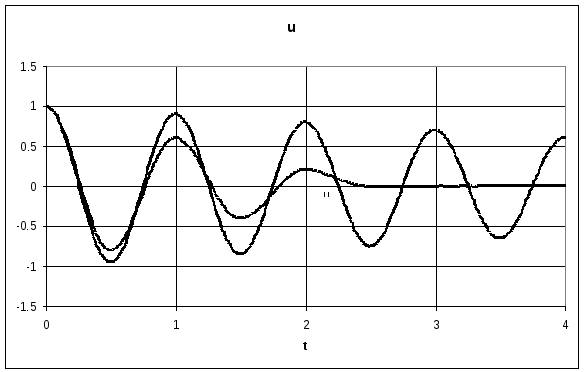
Численное решение при произвольном трении
Численное интегрирование возможно при любом виде функции Ртр. Рассмотрим в качестве примера сухое трение.
Пусть система
выведена из равновесия начальным
смещением
![]()
При пулевой
начальной скорости
![]() ,
а сила трения постоянна и противоположна
направлению скорости движения
,
а сила трения постоянна и противоположна
направлению скорости движения
![]() .
Тогда система (*) в приращениях
.
Тогда система (*) в приращениях
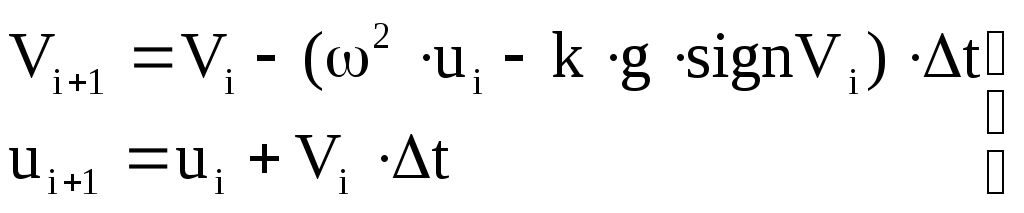 .
.
Система легко
интегрируется в Excel
методом Эйлера. Результаты интегрирования
при собственной частоте f=1
гц и начальном смещении 1 м приведены
ниже. Видно, что с увеличением k
степень затухания растет, а собственная
круговая частота практически не меняется
(![]() ).
Таким образом, вид трения практически
не влияет на частоту собственных
колебаний.
).
Таким образом, вид трения практически
не влияет на частоту собственных
колебаний.