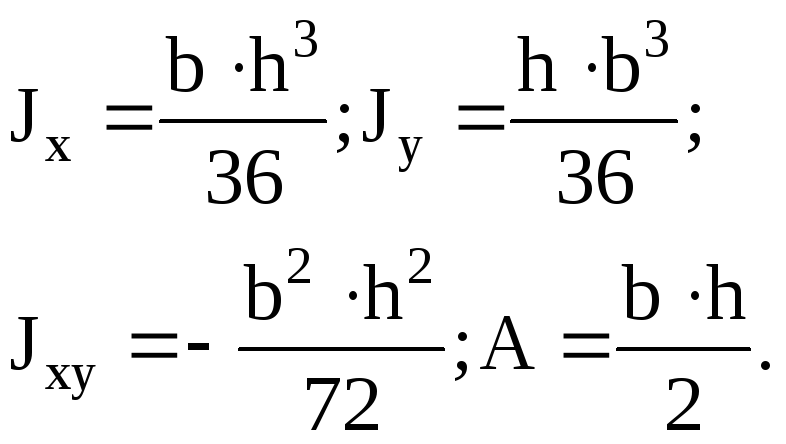6.8 Вычисление перемещений по методу Верещагина
Цель – раскрыть статическую неопределимость методом сил и определить угол поворота сечения z=300 и проверить результаты численным решением. Расчетная схема представлена на рисунке 6.10.
Исходные данные: L=-4 кН∙м, b=300, l=1000 мм, EJX=3,42∙1012/
1.Задача один раз статически неопределима. Эквивалентная схема представлена на рис. 6.10.
L
2. Эпюры изгибающих моментов от внешнего момента и от X1=1
представлены на рис. 6.11.
3.Вычисляем
,
Н∙мм
Численное
решение с помощью шаблона дает
Н∙мм.
Ошибка численного решения
,
что допустимо.
Определяем угол поворота при z=300, для этого в заданной точке прикладываем момент, равный единице. Очевидно, что его эпюра будет как от L=1.
Вычисляем:
Численное решение с помощью шаблона дает
Ошибка численного решения 3,9%, что допустимо.
Рис. 6.12. Эпюры угла и момента из численного решения.
7. Примеры заданий на зачёт или защиту ргр
Примеры заданий для проверки степени усвоения материала и умения пользоватьсмя шаблонами приведены в таблице.
|
№ |
Схема |
Условие задачи |
|
1 |
|
Балка длиной 1 м с равномерно расположенными опорами, нагружена погонной нагрузкой 10 Н/мм, как показано на рисунке. Определить реакции опор. |
|
2 |
|
Балка длиной 1 м нагружена погонной нагрузкой 10 Н/мм на длине 0,7м, как показано на рисунке. Определить размер квадратного сечения из расчета на прочность, [σ]=100 МПа. |
|
3 |
|
Балка длиной 1 м нагружена погонной нагрузкой 10 Н/мм, как показано на рисунке. Подобрать швеллер из расчета на прочность, [σ]=100 МПа. |
|
4 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм. Определить реакции опор. |
|
5 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм. Как изменится максимальный прогиб, если правую опору переместить в центр? |
|
6 |
|
Балка длиной 1 м нагружена силой Р на расстоянии 0,7м от левой опоры как показано на рисунке. Определить коэффициент приведения длины μ в формуле Эйлера. |
|
7 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм и на нее в середине падает груз массой М с высоты Н=200 мм. Определить допустимую массу груза, если [σ]=100 МПа. |
|
8 |
|
Балка длиной 1 м нагружена погонной нагрузкой 30 Н/мм и на нее в середине падает груз массой М=10 кг с высоты Н=200 мм. Подобрать двутавровое сечение из расчета на прочность, если [σ]=100 МПа. |
|
9 |
|
Вал длиной 1 м нагружен погонной нагрузкой 30 Н/мм и по середине крутящим моментом Lк=1 кН·м. Определить допустимый диаметр вала из расчета на прочность, если [σ]=100 МПа. |
|
10 |
|
Вал длиной 1 м и диаметром d=50 мм нагружен погонной нагрузкой 30 Н/мм и по середине крутящим моментом. Определить допустимый крутящий момент из расчета на прочность, если [σ]=100 МПа.
|
|
11 |
|
Балка длиной 1 м с равномерно расположенными опорами нагружена погонной нагрузкой 10 Н/мм. Определит реакции опор.
|
|
12 |
|
Вал длиной 1 м нагружен погонной нагрузкой 10 Н/мм на длине 0,7м. Определить диаметр сечения из расчета на прочность, [σ]=100 МПа.
|
|
13 |
|
Балка длиной 1 м нагружена погонной нагрузкой 10 Н/мм. Подобрать швеллер из расчета на прочность, если [σ]=100 МПа. |
|
14 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм. Определить максимальный прогиб. |
|
15 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм. Как изменятся максимальные напряжения, если правую опору переместить в центр? |
|
16 |
|
Балка длиной 1 м нагружена силой Р на расстоянии 0,5м от левой опоры как показано на рисунке. Определить коэффициент приведения длины μ в формуле Эйлера. |
|
17 |
|
Балка длиной 1 м из двутавра №20 нагружена погонной нагрузкой 30 Н/мм и на нее падает груз массой М с высоты Н=200 мм. Определить допустимую массу груза, если [σ]=100 МПа. |
|
18 |
|
Балка длиной 1 м нагружена погонной нагрузкой 30 Н/мм и на нее падает груз массой М=10 кг с высоты Н=200 мм. Подобрать двутавровое сечение из расчета на прочность, если [σ]=100 МПа. |
|
19 |
|
Вал длиной 0,5 м нагружен по середине крутящим моментом Lк=1 кН·м. Определить допустимый диаметр вала из расчета на прочность, если [σ]=100 МПа. |
|
20 |
|
Вал длиной 1 м и диаметром d=50 мм нагружен погонной нагрузкой и по середине крутящим моментом 1 кН·м. Определить допустимую погонную нагрузку из расчета на прочность, если [σ]=100 МПа. |
8.ПРИЛОЖЕНИЯ
8.1 Геометрические характеристики простых фигур
|
орма поперечного сечения |
Осевые моменты инерции J и площади А |
Момент сопротивления W,
см |
|
|
|
или
|
|
|
|
|
|
|
|
|
|
|
|
в вершине треугольника
в точке основания
|
|
|
|
|
|
|
|
в вершине треугольника
в точке основания
|
или
;
.
.
;
