6.4 Вычисление коэффициента приведения длины в расчете на устойчивость

Цель – определение коэффициента приведения длины в формуле Эйлера

.

.

Исходные данные: схема закрепления стержня и место приложения сжимающей силы представлены на рис.6.7, принять c=0,4l.

1. Для расчета воспользуемся методом неидеальностей, согласно которому любое искажение прямой оси при сжатии критической силой приводит к бесконечным перемещениям. Для этого прикладываем малую погонную нагрузку по всей длине стержня и сжимающую силу в точкеz=c.

2. Формулируем граничные условия

,

и, приняв произвольно длину стержня , силу, сечениеA=100мм, J_X=10000мм⁴, выполняем «Поиск решения» и вычисляем максимальный прогиб в свободной ячейке, напримерV30.

3. В свободной ячейке V31 запоминаем результат из ячейки V30 , т.е .

4. В ячейке V32 вычисляем отношение (=V30/V31)

5. Дополняем в «Поиск решения» изменяемую ячейку D143 (значение Р), в которую вносим значение 1, и ограничение K=100, и выполняем «Поиск решения». В ячейке D143 (при z=700мм) получаем значение критической силы Р_кр.

Считаем, что стократное увеличение прогиба – практически бесконечное перемещение.

6. Вычисляем

.

Правильность решения оценим сравнением с табличным результатом при приложении силы на левом конце - , т.е. найденное значение меньше табличного, что ожидаемо.

6.5 Вычисление допустимой высоты падения груза на нагруженную балку

Цель –определение допустимой высоты падения груза массой две массы балки из стержня (задача 1.3.) в точке, с координатой z=600 мм, п сечением из задачи 1.1.1.

Исходные данные

P, кН	q, Н/мм	L, кН·м	a, мм	с, мм	d, мм	l, мм	b, мм	[σ] МПа	EJх, Н·мм2
7	-10	-4	700	700	1000	1000	300	120	3,4·1012

Расчетная схема представлена на рис.6.8. Удельный вес материала балки .

1. До падения груза стержень имел запас прочности, т.е. нагружение возможно.

2. Поперечную силу от удара вычисляем по формуле

,

где -вес груза груза,

- прогиб балки от статического приложения веса груза.

3. Вычисляем как прогиб ненагруженной балки в точкеz=600 от силы Р_г. Получаем .

4. К нагруженному стержню в точкеz=600 прикладываем поперечную силу , рассчитанную при некотором значении Н, помещенном в ячейкуV14, и добавляем в «Поиск решения» изменяемую ячейку V14 и ограничение запаса прочности величиной 1 (ячейка V11).

5. После выполнения «Поиска решения» в ячейке V14 получаем ответ - H=10,47 мм.

6.6 Вычисление частот собственных поперечных колебаний однородных стержней

Решение с учетом переменного сечения, и прикрепленных масс - тема одного из специальных заданий.

6.6.1 Особенности алгоритма расчета

Задача решается упрощенно: без учета сил сопротивления, движение вдоль оси стержня, инерции поворота сечений.

Масса стержня равномерно сосредотачивается в n точках и, при принятых упрощениях, число степеней свободы колебательной системы также n.

Собственные колебания описываются системой n дифференциальных уравнений второго порядка

. (6.3)

где - поперечные перемещения и их вторые производные по времени в i-той точке,

- масса в i-ой точке, значение ,

–плотность материала стержня,

- взаимные податливости, т.е. поперечные перемещения в j-той точке от единичной поперечной силы, приложенной в i-ой точке.

Взаимные податливости при любом закреплении определяются расчетом по шаблону. Например, для системы с 3 степенями свободы приложив единичную силу в 1-ом направлении (к первой массе) и решив задачу о прогибах, находим перемещения во второй и третьей

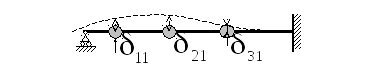
точках. Повторив расчет еще два раза, находим все 9 податливостей.

Точное решение

при численном, т.е. приближенном определении податливостей не выполняется. Поэтому целесообразно принимать в расчет среднее из двух вычисленных значений.

Собственные частоты находим из условия ненулевого решения системы 6. что приводит к алгебраическому уравнению порядкаn относительно .

. (6.4)

В Excel есть стандартная функция - МОПРЕД, которая вычисляет определитель матрицы, например (6.4). Если при вычислении элементов определителя ссылаться на отдельную ячейку, где задано , то «Поиск решения» найдет некоторое, обращающее (6.4) в ноль.

Последовательно изменяя начальное приближение , можно найти всеk его значений круговых частот собственных колебаний.

Частота собственных колебаний в герцах:

.