Назовите причины возникновения и развития теории нечетких множеств и нечеткой логики. [вверх]
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г.
Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
На пути развития нечетких систем принято выделять три периода:
Первый период (конец 60-х–начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман).
Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике.
Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy ApproxiMFtion Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах.
Укажите отличия нечеткого подмножества от четкого. [вверх]
Нечеткое подмножество отличается от обычного тем, что для элементов х из S нет однозначного ответа "да-нет" относительно свойства P. В связи с этим, нечеткое подмножество множества S определяется как множество упорядоченных пар C ={MF(х)/х}, где MF(х) - характеристическая функция (или просто функция принадлежности), принимающая значения из некоторого упорядоченного множества M=[0,1]. Функция принадлежности указывает степень (уровень) принадлежности элемента x подмножеству C. Множество M называют множеством принадлежностей. Если M={0,1}, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.
Раскройте понятие функции принадлежности (характеристической функции). [вверх]
Функция принадлежности - это базовая характеристика нечеткого множества. Обозначим её через MFc(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Сколько значений может принимать функция принадлежности четкого множества. [вверх]
Пусть S - некоторое множество, x - элемент S, а P - некоторое свойство. Обычное (четкое) подмножество A множества S, элементы которого удовлетворяют свойству P определяется как множество упорядоченных пар C ={MF(х)/х}, где MF(х) - характеристическая функция, принимающая значение 1, если х удовлетворяет свойству P, и 0 - в противном случае.
Назовите три основные операции над множествами и их логические аналоги. [вверх]
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение, объединение и отрицание.
Пересечение двух нечетких множеств (нечеткое "И"):
Объединение двух нечетких множеств (нечеткое "ИЛИ"):
Отрицание нечеткого множества (нечеткое «НЕ"):
Запишите математическое выражение объединение двух нечетких множеств. [вверх]
Объединение двух нечетких множеств (нечеткое "ИЛИ"):
A v B: MFAB(x)=max(MFA(x), MFB(x)).
Перечислите атрибуты нечеткой переменной. [вверх]
Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Что такое базовое терм-множество? Приведите примеры множества термов. [вверх]
Базовое терм-множество Т – это множество значений лингвистической переменной. Элементы базового терм-множества представляют собой названия нечетких переменных. Например, есть лингвистическая переменная "Цена акции". Ее базовое терм-множество будет состоять из трех нечетких переменных: "Низкая", "Умеренная", "Высокая", а область рассуждений задана в виде X=[100;200] (единиц).
Перечислите три основные функций принадлежности нечётких множеств и нарисуйте их графики. [вверх]
Треугольная, трапецеидальная и гауссова функции принадлежности.
Какими параметрами описывается функция принадлежности гауссова типа. [вверх]
Функция принадлежности гауссова типа описывается формулой:
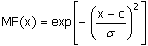
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр σ отвечает за крутизну функции.
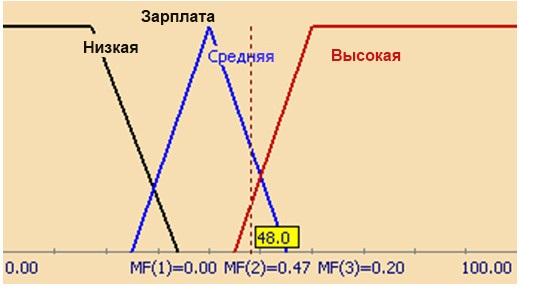
Изобразите совокупность графиков функций принадлежности всех термов лингвистической переменной "Величина зарплаты" (число термов выбирается произвольно). [вверх]
"Величина зарплаты" (число термов выбирается произвольно).
Какие условия должны соблюдаться полноты базы нечетких правил. [вверх]
1.Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.
2.Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
Перечислите 4 этапа нечеткого логического вывода. [вверх]
В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация.
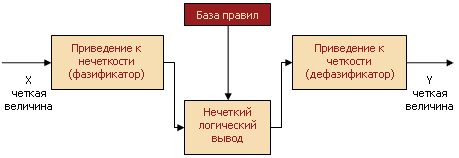
Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.
Изобразите модель искусственного нейрона и укажите на рисунке его составные части. [вверх]
Нейрон (нервная клетка) состоит из тела (cell body), или сомы (soma), и отростков нервных волокон двух типов - дендритов (dendrites), по которым принимаются импульсы, и единственного аксона (axon), по которому нейрон может передавать импульс.
Нейрон получает сигналы (импульсы) от аксонов других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль своего аксона (передатчика), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся специальные образования - синапсы (synapses), которые влияют на величину импульсов.
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются химические вещества, щель, возбуждая или затормаживая, в зависимости от типа синазываемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую напса, способность нейрона-приемника генерировать электрические импульсы.
Результативность передачи импульса синапсом может настраиваться проходящими через него сигналами так, что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека.
1.Нейроны, выходные сигналы которые поступают на вход данному нейрону;
2.Сумматор входных сигналов;
3.Вычислитель передаточной функции;
4.Нейроны, на входы которых подаётся выходной сигнал данного;
В этой модели нейрона можно выделить три основных элемента:
синапсы, каждый из которых характеризуется своим весом или силой. Осуществляют связь между нейронами, умножают входной сигнал на весовой коэффициент синапса, характеризующий силу синаптической связи;
сумматор, аналог тела клетки нейрона. Выполняет сложение внешних входных сигналов или сигналов, поступающих по синаптическим связям от других нейронов. Определяет уровень возбуждения нейрона;
функция активации, определяет окончательный выходной уровень нейрона, с которым сигнал возбуждения (торможения) поступает на синапсы следующих нейронов.