Геологи(1 курс). Математика. / Тема_15_НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

119

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

I. Первообразная, понятие неопределенного интеграла.

При введении понятия производной данной функции нами была рассмотрена задача о нахождении мгновенной скорости точки по известному закону ее движения S= S(t) . В механике встречается обратная задача: по известному закону изменения скорости V= V(t) найти закон движения, то есть найти такую функцию S= S(t) производная которой равна V(t) . Эта задача приводит к понятию первообразной функции.

Определение: функция F(x) называется первообразной для функции f(x) на

интервале (a, b) , если функции f(x) и F(x) определены на этом

интервале, функция F(x) дифференцируема на интервале (a, b) и в

каждой точке интервала выполняется равенство

(1)

Первообразная существует для любой функции, непрерывной на отрезке.

Теорема: если F₁(x) и F₂(x) - две первообразные для функции f(x) на интервале

(a, b), то они отличаются только на константу, то есть

(2)

где C - постоянная.

Доказательство:

Обозначим и найдем производную этой функции

По определению первообразной и в соответствии с условием теоремы

и .

Тогда , откуда следует, что , что и требовалось доказать.

Из теоремы следует, что если известен

график одной из первообразных F₁(x)

для функции f(x) , то графики всех других

первообразных для данной функции

получаются из первого сдвигом вдоль оси Oy.

Совокупность всех первообразных для функции f(x) на некотором промежутке называют неопределенным интегралом от функции f(x) на этом промежутке и обозначают

(3)

где F(x) - какая-нибудь первообразная функции F(x) ,

C - произвольная постоянная.

Знак называют знаком интеграла, f(x) – подынтегральной функцией,

- подынтегральным выражением. Поскольку , подынтегральное выражение можно записать

Операцию нахождения неопределенного интеграла от данной функции

называют интегрированием. Интегрирование является операцией, обратной дифференцированию. Используя любую формулу для производной , можно записать, что . Например, зная, что , получим

II. Свойства неопределенного интеграла.

Перечислим основные свойства неопределенного интеграла, вытекающие из определения (3) и равенства (4):

свойство 1: (5)

т.к.

свойство 2: (6)

т.к.

свойство 3: (7)

Свойства (1) и (3) показывают, что знаки дифференциала и интеграла, стоящие рядом, взаимно уничтожаются.

свойство 4: (свойство линейности неопределенного интеграла):

. (8)

Соотношение (8) можно доказать, дифференцируя его правую и левую части с учетом свойства линейности для производных и равенства (6):

Константа может быть вынесена за знак интеграла, интеграл суммы равен сумме интегралов.

свойство 5:(свойство инвариантности формы неопределенного интеграла):

если , то какова бы ни была функция u= u(x) , справедливо соотношение (9)

Это свойство является следствием инвариантности формы первого дифференциала. Дифференцируя (9), на основании (5) получаем

Пример. Известно, что

Тогда на основании свойства 5 получим

III. Простейшие приемы интегрирования. Таблица интегралов.

Простейшие приемы интегрирования основаны на использовании

свойств (1)-(4) неопределенного интеграла и таблицы интегралов,

построенной с помощью таблицы производных. Простейшие приемы интегрирования составляют так называемое непосредственное интегрирование.

Непосредственное интегрирование заключается в проведении тождественных преобразований подынтегрального выражения с целью получения суммы табличных интегралов.

Приведем таблицу неопределенных интегралов:

Рассмотрим примеры непосредственного интегрирования:

1. 

2. 

3)

4)

IV. Метод замены переменной.

Интегрирование методом замены переменной основано на свойстве

инвариантности формы неопределенного интеграла и может осуществляться в двух вариантах:

а) интегрирование подведением под знак дифференциала.

этот вариант метода используется в том случае, если подынтегральная

функция является сложной и в подынтегральном выражении удается

выделить производную промежуточного аргумента . Тогда

(10)

В соотношении (10) функция u(х) подведена под знак дифференциала.

Примеры:

1)

2)

3. .

б) метод подстановки - используется в том случае, когда переход к новой переменной позволяет существенно упростить подынтегральную функцию.

Пусть требуется найти . Перейдем к переменной u , используя подстановку . Тогда

, а

(11)

Примеры:

1)

Выполним подстановку , ,

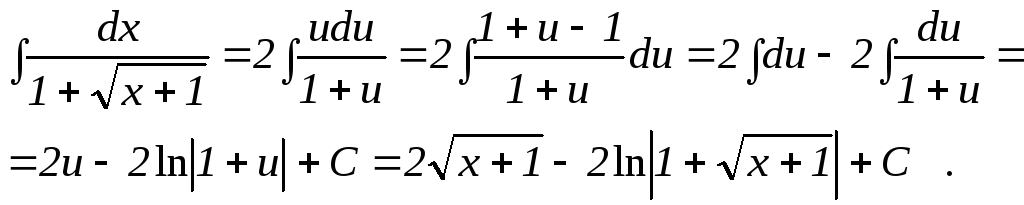
2)

Подстановка

V. Метод интегрирования по частям.

Метод интегрирования по частям основывается на формуле дифференцирования произведения двух функций u= u(x) и v= v(x) :

. (a)

Пусть подынтегральная функция представляет собой произведение функции u(x) на производную от функции v(x) . На основании равенства (а) можно записать

Тогда (б)

Переходя в (б) к дифференциалам, получим

и на основании (7)

(12)

или в равносильной форме

(12)

Формула (12) называется формулой интегрирования по частям.

Рассмотрим некоторые случаи, в которых целесообразно применение

формул (12), (12'):

1) подынтегральная функция представляет собой произведение многочлена P_n(x) на e^ax или . т.е.

или

В этом случае удобнее принять или , или

Пример:

2) подынтегральная функция представляет собой произведение многочлена P_n(x) на

В этом случае полагают или

Пример:

3) подынтегральная функция - произведение показательной функции на или . В этом случае формулу интегрирования по частям применяют дважды.

Пример:

Тогда

При двукратном применении формулы интегрирования по частям целесообразно в качестве u(x) и u₁(x) , v(x) и v₁(x) принимать одни и те же функции (показательную либо тригонометрическую). В противном случае после подстановки интеграла I₂ получим тождество I₁=I₁ .