Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский государственный национальный исследовательский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория_линейных_электрических_цепей_Ч1

.pdf

Скачиваний:

310

Добавлен:

30.03.2015

Размер:

3.42 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2824 25 26 27 28 > Следующая >>>

ратов и машин энергия в них поступает из электрической сети равномерно и вибрации в этих устройствах снижаются. Необходимо отметить, что постоянство мгновенной мощности наблюдается, как правило, только при симметричном режиме трехфазной цепи.

6.5. Круговое вращающееся магнитное поле трехфазного тока

При протекании тока по катушке в направлении, указанном

на рис. 6.31, вектор магнитной индукции B в соответствии с правилом буравчика направлен вверх. Если изменить направление тока на

противоположное, то вектор B также изменит направление на противоположное. Таким образом, магнитное поле изменяется (пульсирует) вдоль оси катушки, такое магнитное поле называют пульсирующим.

При изменении тока по синусоидаль-

Рис..66..3131


ному закону i = Im sin ω			t вектор B изменяет свое направление дваж-
ды за период. При этом модуль				B тоже является синусоидальной
функцией B = Bm sin ω			t . Таким образом, B при данных условиях в
пространстве		может	принимать		B1 (1)
два	противоположных направле-

ния, а во времени изменяться по					3
гармоническому закону (магнит-
ное поле, пульсирующее по гар-					1
моническому закону).
	Разместим одинаковые ка-			B3 (3)	B2 (2)
тушки 1, 2, 3		так, чтобы их оси
были смещены в пространстве на					2

120°	относительно		друг друга		Рис. .66.32.32
(рис. 6.32).

231

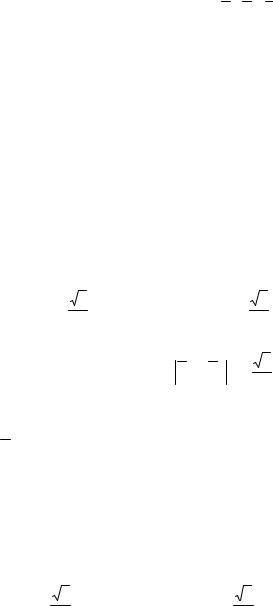
Зададим положительное направление векторов B1, B2 , B3 ка-

ждой катушки так, как это показано на рис. 6.32 при указанных направлениях токов. При подключении катушек к трехфазной цепи

i1 = Im sin ω

i2 = Im sin(ω t −120D);

i3 = Im sin(ω t − 240D).

При этом модули вектора магнитной индукции каждой ка-

тушки изменяются:

B1 = Bm sin ω t; B2

= Bm sin(ω

t −120D);

B3 = Bm sin(ω t − 240D) .

Найдем сумму

1 +

2 +

для моментов времени t,

со-

ответствующих условиям ω t = 0;

; π ;

π .

При ω t = 0

B1 = 0;

B2 = Bm sin(−120D )= −

3 Bm ;

= Bm sin(− 240D )=

3 Bm .

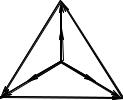
Векторная диаграмма

для данного момента времени пред-

ставлена на рис. 6.33,

а. Модуль вектора

B = B2 + B3 = 2

3 B

×cos 30D = 1,5Bm .

2.При ω t = π

B1 = Bm

; B2 = Bm sin(− 30D )= −

;

B3 = Bm sin(− 210D )= −

Векторная диаграмма представлена на рис. 6.33, б. Модуль

вектора B =

+ B2 + B3

= Bm 1 +

cos 60D +

cos 60D = 1,5Bm .

При ω t = π

B1 = 0;

= Bm sin 60D = 3 Bm ;

B3 = Bm sin(− 60D )= − 3 Bm .

232

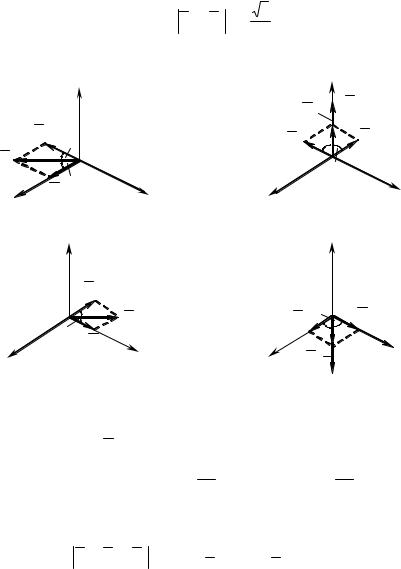
Векторная диаграмма для этого случая представлена на

рис. 6.33, в. Модуль вектора B = B2 + B3					= 2	3 Bm cos 30D			=1,5Bm .
						2
	1							1
	1
							B1		B
							B1
	B 2 30°						B2		B3
B	30°							60°
								60°
									2
3	B3		2			3			2
3	а		2			3			б
	а								б
	1							1
		B3					60°
							60°		B2
	30°		B				B3		B2
3	30°	B2	2			3	B1		2
									2

	в							г
			Рис. 6.33					г
			Рис. 6.33
	4. При ω	t = 3 π
		2
	B1 = −Bm ;	B2 = Bm sin150D = Bm ;			B3	= Bm sin 30D		= Bm .
				2					2
	Для этого момента времени справедлива векторная диаграм-
ма, представленная на рис. 6.33, г. Модуль вектора
	B = B1 + B2			1			1		= 1,5Bm .
	B = B1 + B2		+ B3 = Bm 1 +	cos 60D +			cos 60D		= 1,5Bm .
				2			2

233

Если ток Im sin(ω t −120D) пропустить по третьей катушке, а ток Im sin(ω t +120D) – по второй катушке, то направление вращения

поля изменится на обратное.

Если произойдет обрыв одной из фаз или ток в ней по амплитуде не будет равен току в какой-либо другой фазе или сдвинут по фазе не на 120D , то образуется эллиптическое вращающееся магнит-

ное поле, результирующей вектор магнитной индукции которого описывает эллипс и имеет переменную угловую скорость.

Для усиления вращающегося магнитного поля внутрь катушек помещают полый или сплошной ферромагнитный цилиндр, а стороны катушек заключают в пазы внешнего ферромагнитного цилиндра.

Эффект вращающегося магнитного поля используется для создания асинхронных и синхронных трехфазных двигателей.

6.6. Задачи и вопросы

Типовые задачи

Задача 1.

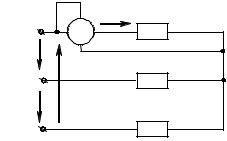
Дано: к зажимам симметричного трехфазного генератора (рис. 6.34) подсоединена симметричная нагрузка. Ваттметр, включенный в фазу А, показывает 40 Вт.

	* I A	R	Найти: показания
A			ваттметра в случае:
	* W
			а) обрыва фазы В;
U AB
		R	б) короткого замы-
B			кания фазы В.
	U	O1
			Решение
U BC	CA	R	Мощность,	потреб-
C
			ляемая фазой А и фикси-

		Рис. 6.34	руемая ваттметром,
		. 6.34
			PA = U AO1 I A cos ϕ	н .

234

В качестве нагрузки используется резистор, следовательно, cos ϕ н = 0 . Чтобы определить показание ваттметра, необходимо уз-

нать, как изменятся напряжение и ток по сравнению с их значением в симметричном режиме. Для этого предварительно построим векторную диаграмму для симметричной нагрузки (рис. 6.35).

Порядок построения диаграммы:

•потенциалы точек A, B, C располагаем в вершинах равностороннего треугольника линейных напряжений генератора;

•потенциал нейтральной точки О генератора находится в центре тяжести этого треугольника;

•потенциал нейтральной точки О1 нагрузки в силу ее симметрии

	( Z a = Z b = Z c = R ) совпадает с						U aO1 (EA )
	потенциалом точки О;						U aO1 (EA )
•	фазные напряжения на нагруз-						I	U
	ке совпадают с фазными на-					UCA	I	U
	пряжениями генератора;					UCA	A		AB
	пряжениями генератора;						O(O1)
•	ток в фазе нагрузки равен со-						O(O1)
•	ток в фазе нагрузки равен со-							I
	ответствующему фазному				на-		IC	B
	пряжению, деленному			на	со- U cO	(EC )	U BC		UbO	(EB )
	противление нагрузки,				1				1
	противление нагрузки,			в част-			Рис. 6..35
	ности: I A =	UaO1					Рис. 6..35
		UaO1	.
			.
		R

Обрыв фазы B

В результате обрыва фазы нагрузка становится несимметричной и между нейтральными точками нагрузки и генератора появляется напряжение смещения нейтрали, которое может быть определено в соответствии с (6.19):

UO1O	=	EA Y a + EB Y b + EC Y c	;

		Y a + Y b + Y c + Y o

235

Y o = 0; Y b = 0; Y a				= Y c	=	1	;
Y o = 0; Y b = 0; Y a				= Y c	=		;
	E	+ E				R
UO O =	E	+ E
	A	C	,
		2	,
1

UaO1

I A

IC UO1O O

UcO1

Рис. 6.36 Рис. 6.36

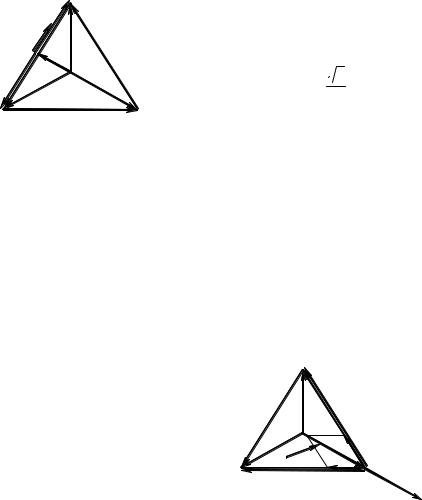
т.е. нейтральная точка O1 нагрузки сместится в середину линейного напряжения UCA (рис. 6.36). Следовательно, фазное напряжение на нагрузке в фазе А (а, значит, и ток в этой фазе) изменится по сравнению с

симметричным режимом в 3 раз. 2

Мощность фазы А изменится в 3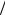4 раза и ваттметр покажет 30 Вт.

Короткое замыкание фазы В

При коротком замыкании фазы В потенциал точки О1 станет равным потенциалу точки В. Это подтверждает следующий расчет:

+ E

;

O1O

Y a

+ Y b

+ Y c + Y o

Y o = 0; Y b = ∞ ; Y a

= Y c

;

UO O = EB .

Этот результат получается

UaO

при раскрытии неопределенности

по правилу Лопиталя.

Векторная диаграмма для

случая короткого замыкания фазы

В представлена на рис. 6.37.

O O

Напряжение фазы А опре-

UcO1

Рис. 6.37

деляется по формуле:

Рис. 6.37

236

UaO1 = EA −UO1O = EA − EB = EAB ,

следовательно, по сравнению с симметричным режимом напряжение на нагрузке фазы А увеличивается в 3 раз, аналогичным образом изменится и ток в фазе А. Показание ваттметра увеличится в 3 раза, следовательно, ваттметр покажет 120 Вт.

Задача 2

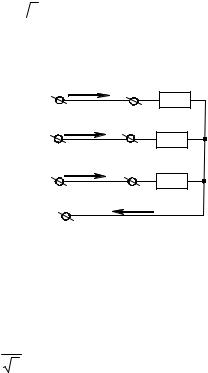
Дано: для схемы (рис. 6.38)

линейное	напряжение	симметрич-
ного генератора Uл = 380		В,	сопро-
тивления	фаз нагрузки	Z a	= 11 Ом,
Z b = Z c = 22 Ом.

Найти: токи при наличии и обрыве нейтрального провода.

Ia	a	Z a
A
Ib	b	Z b	О1
B			О1
Ic	c	Z с
C	I N
O	I N
O

Решение	Рис. 6.338
	. 6.
При наличии	нейтрального

провода с нулевым сопротивлением напряжение смещения нейтрали равно нулю и фазные напряжения на нагрузке совпадают с фазными напряжениями генератора:

Uф

= U л = 220 В.

Фазные напряжения:

UaO = 220 В, UbO

= 220e− j120D В, UcO

= 220e− j 240D В.

Токи в фазах:

Ia =

UaO

220

= 20 А, Ib =

UbO

= 10e− j120

А,

Z a

Z b

UcO1

= 10e− j 240D А.

Z c

237

Ток в нейтральном проводе определяется по I закону Кирх-

гофа:
I N = Ia + Ib		+ Ic = 20 +10e− j120D +10e− j 240D = 10 А.
Векторная диаграмма представлена на рис. 6.39.
UaO				UaO
	1				1
	I			I
	I		I	a	O1
	a		I		O1
IN	O(O1)		c		I
I	I			O	b
				O

c	b
UcO		U	UcO		U
1		bO	1		bO
		1	1		1
Рис. 6.39			Рис. 6.40

При обрыве нейтрального провода смещение нейтрали в со-

ответствии с формулой (6.20):

	1		1				− j120D				1		− j 240D
	220	+			e				+			e
	220	+			e				+			e
UO1O =	11		22								22			= 55e	j 0
UO1O =			1	+		1		+		1				= 55e
				+				+	22
		11			22				22

Напряжения на фазах нагрузки:

UaO	= U AO		−UO O = 220 − 55 = 165 В;
1			1
UbO	= U BO		−UO O		= 220e− j120D − 55 = 250e− j131D В;
1			1
UcO	= UCO		−UO O		= 220e− j 240D − 55 = 250e j131D В.
1			1
Фазные токи:
Ia =	UaO		165	= 15 А, Ib =		UbO		250e− j131D
	1	=				1	=		= 11,4e
			11					22
	Z a					Z b

В.

− j131D А

238

Ic	=	UcO1	=	250e j131D	= 11,4e j131D А.
		Z c
			22

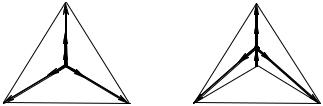
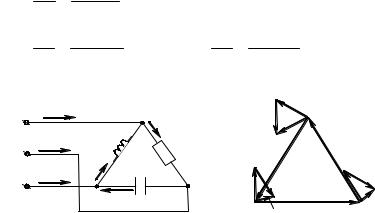
Векторная диаграмма представлена на рис. 6.40.

Задача 3.

Дано: для схемы (рис. 6.41) линейное напряжение симметричного генератора Uл = 380 В, сопротивления фаз нагрузки

Z ab = 38 Ом, Z bc = 38e− j 90D = − j38 Ом, Z ca = 38e j 90D = j38 Ом.

Найти: линейные и фазные токи.

Решение

Фазные напряжения на нагрузке равны линейным напряжениям генератора:

U AB = 380e j 30D В; U BC = 380e− j 90D В; UCA = 380e j150D В.

Фазные токи определяются по закону Ома:

Iab

= Uab

= 380e j 30D

= 10e j 30D

Z ab

Ibc

= Ubc

= 380e

− j 90D

= 10 A;

Ica

= Uca

= 380e

j150D

= 10e j 60D

Z bc

38e− j 90

Z ca

38e j 90

I A

− I bc

I B

X L

U ca

U ab

−

I ab

− I ca

X C

C I B

U bc

Рис. 6.41

Рис. 6.42

Линейные токи определяются по I закону Кирхгофа:

239


I A	= Iab − Ica		= 10e j 30D	−10e j 60D = 5,18e− j 45D			A;
IB	= Ibc	− Iab	= 10 −10e j 30D = 5,18e− j 75D			A;
IC	= Ica	− Ibc	= 10e j 60D	−10 = 10e− j120D	A.

Векторная диаграмма представлена на рис. 6.42.

Вопросы и упражнения для самоконтроля

1.Каково численное соотношение между фазовыми и линейными напряжениями при соединении шестифазного симметричного приемника звездой?

2.Нагрузка питается симметричной трехфазной системой. Симметричную нагрузку, соединенную звездой без нейтрали, пересоединили в треугольник при неизменном линейном напряжении. Как изменится линейный ток, активная мощность?

3.Всегда ли при симметричной системе фазных ЭДС симметрична система линейных ЭДС на генераторе, на нагрузке?

4.При каком способе соединения трехфазных цепей:

а) фазные токи одновременно являются линейными; б) фазные напряжения одновременно являются линейными? 5. Верно ли утверждение:

а) трехфазный источник, фазы которого соединены звездой, симметричен, если EA = EB = EC ;

б) трехфазный источник, фазы которого соединены треугольником, симметричен, если EAB = EBC = ECA ;

в) трехфазный приемник, фазы которого соединены звездой, симметричен, если Z a = Z b = Z c ;

г) трехфазный приемник, фазы которого соединены звездой, симметричен, если Za = Zb = Zc ?

6. Симметричный трехфазный приемник, соединенный в треугольник, имеет сопротивление фазы Z1 = 15 Ом. Другой симметричный приемник соединен в звезду и подключен к той же сети. Извест-

240

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 2324 / 2824 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.03.201518.9 Кб21теория государства и права.docx
#
16.04.20191.18 Mб160Теория и методология истории. Курс лекций. Лапт....doc
#
05.08.201939.75 Кб17Теория инноваций.docx
#
30.03.201528.49 Кб17Теория организации. Шпоры.docx
#
26.09.2019116.22 Кб3Теория организации.doc
#
30.03.20153.42 Mб310Теория_линейных_электрических_цепей_Ч1.pdf
#
30.03.201564.36 Кб45терминальные состояния и клиническая смерть.docx
#
11.08.2019242.18 Кб12Термины и понятия по геоморфологии_Анисимов.DOC
#
24.11.2018111.8 Кб6Термины ИГПЗС.docx
#
29.03.2015270.34 Кб18Термины.doc
#
29.03.201553.25 Кб155тест гормоны.doc