23. Метод ветвей и границ. Решение задачи коммивояжера.

Пусть Q– задача минимизации

S– множество допустимых решений

φ(S) – качество решения

Задача: найти S* такое, чтоφ(S*) – минимальное.

Метод:

Разбиваем Sна подмножества. Для всех подмножеств строится оценкатакое, что. Если найденотакое, что, то все решения израссматривать не нужно.

Задача коммивояжера:

Дано: матрица расстояний

-1

1) а) редукция по строкам

б) редукция по столбцам

2) суммарная редукция (оценка корня) =6

3) считаем вторичные штрафы (второй по величине элемент строки или столбца)

4 – максимальный вторичный штраф

4) выбираем максимальный вторичный штраф. Берем нулевое значение в этой строке или столбце. Ветвление по ребру, соответствующему выбранному элементу.

5) оценки:

Правый:оценка корня + вторичный штраф

Левый:вычеркиваем из матрицы соответствующую строку и столбец. Заменяем обратное ребро на ∞. ВАЖНО! Сохранить нумерацию столбцов и строк

1 – максимальный вторичный штраф

Суммарная редукция =0. Максимальный вторичный штраф 1.

4

Итоговый цикл:2→3→4→1→2

Примечание: необходимо контролировать, чтобы не образовывалось циклов длиной меньше n.

24. Вероятностные алгоритмы. Класс BPP. Вероятностный алгоритм поиска максимального элемента.

Вероятностные алгоритм– это алгоритм, в котором помимо детерминированных действий присутствуют случайные события, т.е. алгоритм, который будет зависеть от каких-то вероятностей.

Расширяется класс решаемых задач.

Вероятностная машина Тьюринга (ВМТ) – машина Тьюринга, в которой каждое правило имеет вид:

Каждому переходу соответствует некоторая вероятность, такая что

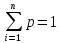
BPP- класс – (для задач распознавания) задача распознавания Q принадлежит классу BPP, если существует ВМТ М и полином р(), а также некоторое вещественное число c> 0,5, такие что машина М остановится за время не превосходящее p(|x|):

• Если Q(x)=1, то ВМТ М даст ответ «да» с вероятностью больше с

• Если Q(x)=0, то ВМТ М даст ответ «нет» с вероятностью больше с.

Замечание:

Если Q € BPP, то многократным запуском ВМТ можно добиться получения правильного ответа с вероятностью 1-q^n, где q=2*sqrt(c(1-c)),n– количество запусков ВМТ.

Чем больше с, тем быстрее это выражение будет стремиться к 1.

Пример: Вероятностный алгоритм поиска max элемента в массиве

Пусть k сравнений заменены на «подбрасывание монеты», тогда оптимальный вероятностный алгоритм получается из обычного линейного алгоритма путем замены k первыхсравнений. В этом случае вероятность правильного ответа р определяется по формуле р=(n-k)/n

Утверждение: вероятность (n-k)/nявляется неулучшаемой точной верхней оценкой вероятности правильного решения задачи поиска max элемента с заменой k сравнений.

Утверждение 1: Класс P содержится в классе ВРР

Утверждение 2: Класс ВРР является более широким, чем Р

25. Самокорректирующиеся алгоритмы. Самокорректирующийся алгоритм сортировки.

Самокорректирующиеся алгоритмы – это алгоритмы, которые правильно и точно решают задачу даже при наличии сбоев (т.е. ошибок при выполнении)

Задача сортировки массива.

Предположим, что ошибки возможны при сравнении элементов массива. Причем, всего возможно <=k ошибок. N- число элементов в массиве.

Алгоритм:

1. Отсортировать массив с помощью алгоритма слияние. Полученный массив обозначим pi(0)

2. Повторить 2k раз шаги:

1. Верификация – последовательный просмотр pi(i) и сравниваем попарно его элементы:a(1) иa(2),a(2) иa(3), т.д. В массиве pi(i) до тех пор пока не найдем пару a(j)>a(j+1). Такая пара (ошибка) называетсяинверсией.

• Если инверсия найдена, то запоминаем в t номер j и переходим к шагу 2.2

• Если инверсия не найдена, то полагаем pi(i+1)=pi(i) и переходим к следующей итерации

1. Если найдена инверсия – исправление. Массив pi(i) разрезается на 2 части в одну a(1)..a(t), а во вторую a(t+1)..a(n). Эти две части сливаются по алгоритму слияния, образуя массив pi(i+1). Переходим на следующий шаг итерации.

3. Получили 2k+1 массив: pi(0) и pi(1), …,pi(2k). Согласно теореме, среди них ищем повторяющийся min k+1 раз массив – он и является ответом.

Пример:

m=(6, 4, 3, 8, 1, 2, 7, 5) k=3

1. 4, 6 3,8 -> 3, 8, 4, 6 (допущена первая ошибка)1,2 5,7 -> 1, 2, 5, 7pi(0) = 1, 2, 3, 5, 7, 8, 4, 6

2. 1, 2, 3, 5, 7, 8, 4,6pi(1) = 1, 2,4, 3, 5, 6, 7, 8 (допущена вторая ошибка) pi(2) =1, 2, 3, 4, 5, 6, 7, 8 (допущена третья ошибка)pi(3) = 1, 2, 3, 4, 5, 6, 7, 8pi(4) = 1, 2, 3, 4, 5, 6, 7, 8pi(5) = 1, 2, 3, 4, 5, 6, 7, 8pi(6) = 1, 2, 3, 4, 5, 6, 7, 8

3. Среди 7 массивов 5 одинаковых.

Оценим сложность:

1. O(n*logn)

2. 2k((n-1)+n)=2k(2n-1) - O(nk)

3. O(nk)

t(α)= O(n*log n + nk)

Следствие:

Если k пропорционально log n , то самокорректирующийся алгоритм имеет такой же порядок роста функции сложности как и алгоритм без коррекции.

Для задачи поиска max элемента оптимальным самокорректирующимся алгоритмом является алгоритм тривиального дублирования.