
Ответы на все вопросы по линейной алгебре
.docx204.симметрической квадратичная матрица называется если аij=аji, то есть если равны элементы матрицы симметричные относительно главной диагонали
205.свойства собственных чисел и векторов симметрической матрицы: все собственные числа симметрической матрицы действительные, собственные векторы симметрической матрицы ортогональны
206.матрицей
квадратичной формы называется
симметрическая матрица

207.каноническим видом квадратичной формы называется вид f(х1,х2,х3)=к1
208. Выписать матицу КФ
Составить харакетр. Уравнение
Найти собственные значения
Найти для каждой 𝝀 значения матрицы ( то есть собственный вектор) нормировать вектор
Составить матрицу перехода и найти (x,y,z)
209. Квадратичная форма называется положительно (отрицательно) определённой, если для любого выполнено неравенство .
210. Критерий Сильвестра определяет, является ли квадратная матрица положительно (отрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу (aij). Тогда эта форма положительно определенна, если и только если все её угловые миноры Δi положительны, и отрицательно определенна, если и только если их знаки чередуются, причём Δ1 < 0.< 0, и неотрицательно определена если и только если все её главные миноры неотрицательны.
211. комплексным числом Z наз.упорядоченная пара действительных чисел (a,b):z=(a,b).
212. а=ReZ - действительная часть комплексного числа z, а b=Imz – мнимая часть z.
213. алгебраическая форма комплексного числа z=a+ib.
214.
правила действий над комплексными
числами в алгебраической форме :
Сложение и умножение комплексных чисел
производится по правилам сложения и
умножения алгебраических многочленов;
учитывая при этом, что ![]()
![]() ,
, ![]() и
т. д.: Правило
сложения. При
сложении комплексных чисел складываются
действительные и мнимые части
соответственно.
Правило
вычитания. При
нахождении разности комплексных чисел
из действительной и мнимой частей
уменьшаемого вычитаются
соответственно действительная и мнимая
части вычитаемого.
Правило умножения. Комплексные
числа перемножаются как двучлены, при
этом учитывается, что
и
т. д.: Правило
сложения. При
сложении комплексных чисел складываются
действительные и мнимые части
соответственно.
Правило
вычитания. При
нахождении разности комплексных чисел
из действительной и мнимой частей
уменьшаемого вычитаются
соответственно действительная и мнимая
части вычитаемого.
Правило умножения. Комплексные
числа перемножаются как двучлены, при
этом учитывается, что ![]() .Правило
деления. Чтобы
разделить число
.Правило
деления. Чтобы
разделить число ![]() (
(![]() ),
следует числитель и знаменатель
дроби
),
следует числитель и знаменатель
дроби ![]() умножить
на число
умножить
на число ![]() ,
сопряженное знаменателю
,
сопряженное знаменателю
215. комплексное число Ž=a+ib называют комплексно-сопряжённым числу z=a+ib.
216. Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
217.
аргументом числа z
называется угол  (в
радианах) радиус-вектора точки,
соответствующей числу z,
(в
радианах) радиус-вектора точки,
соответствующей числу z,
218. тригонометрическая форма записи комплексного числа z= ρ(cosψ + i sinψ).
219.
умножение двух комплексных чисел в
тригонометрической форме
z1z2= 1
1 2(cos(
2(cos( 1+
1+ 2)+isin(
2)+isin( 1+
1+ 2))
2))
220.
деление двух комплексных чисел в
тригонометрической форма
z1/z2= 1/
1/ 2(cos(
2(cos( 1-
1-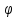 2)+isin(
2)+isin( 1-
1- 2))
2))
221. zn= ρn(cosψ + i sinψ) – формула Муавра.
222.
комплексное число z1=n называется корнем n-степени
из z,если
z=zn
1.
называется корнем n-степени
из z,если
z=zn
1.
223. показательная форма комплексного числа Z=ρeiψ.
224. Эллипс-множество точек плоскости,сумма расстояний от которых до двух данных точек,называемых фокусами эллипса-const.
225. координаты эллипса : Если обозначить расстояние между фокусами F1 и F2 через 2с, тогда координаты фокусов будут соответственно (-с, 0) и (с, 0).
226. каноническое уравнение эллипса : (x2/a2)+(y2/b2)=1
227.эксцентриситетом эллипса называется число ξ=c/a, т.к. для эллипса c<a, то эксцентриситет <1.
229. гипербола – множество точек плоскости, разность расстояния от которых до двух данных точек называемых фокусами гиперболы есть величина постоянная равная 2а.
230.координаты
фокуса гиперболы Точки F1(-c;0) и F2(c;0) называются
фокусами гиперболы.
Здесь c=
231.каноническое уравнение гиперболы (x2/a2)-(y2/b2)=1
232.
уравнение асимптот гиперболы(x/a) (y/b)=0;
y=
(y/b)=0;
y= (b/a)*x
(b/a)*x
233.эксцентриситет
гиперболы
 =с/а
=с/а
235. парабола- множество точек плоскости равноудалённых от данной точки F-фокуса и от данной прямой d- директриса параболы.
236. координаты фокуса параболы: точка F(p/2, 0) — фокус;
237.каноническое уравнение параболы у2=2px
238. уравнение директрисы параболы: прямая x = −p/2 — директриса
240.поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 в котором по крайней мере один из коэффициентов a11, a22, a33, a12, a23, a13 отличен от нуля.
241. каноническое уравнение эллипсоида(x2/a2)+(y2/b2)+(z2/c2)=1
242.
каноническое уравнение однополостного
гиперболоида :
![]()
243. каноническое уравнение двуполостного гиперболоида:(x2/a2)+(y2/b2)-(z2/c2)=-1
244.
каноническое уравнение конуса второго
порядка:
![]()
245.
каноническое уравнение эллиптического
параболоида:
![]()
246.
каноническое уравнение гиперболического
параболоида:
![]()
247.
каноническое уравнение эллиптического
цилиндра:
![]()
248.
каноническое уравнение гиперболического
цилиндра:
![]()
249.
каноническое
уравнение
параболического
цилиндра:
![]()
