МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО

ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ.

Пермский государственный университет

Кафедра общей физики

Определение скорости звука в воздухе

Методическое руководство к лабораторной работе №12

Введение

Звуковые колебания представляют собой периодические чередования сжатий и разрежений в газе (продольную волну). При этом в общем случае, изменение давления газа происходит по закону политропы

Pv^γ = const , P = const ρ^γ

где ρ - плотность газа, а показатель у зависит от скорости теплообмена между

областями сжатия и разрежения. В идеальном газе предельными случаями

являются изотермический процесс (γ=1), когда температура выравнивается

мгновенно, и адиабатный процесс, когда теплообмен между областями

отсутствует (γ =Ср/Сv, где Ср и Сv- изобарная и изохорная теплоемкости газа).

Вид реального процесса можно определить экспериментально, измерив, скорость звука в газе. Если считать процесс изотермическим (γ =1), то скорость звука равна:

(1)

Если же колебания происходят адиабатно (γ =Ср/Сv), то имеем

(2)

Измерение скорости звука в воздухе в данной работе основано на использовании свойств стоячих волн. Стоячей волной называется волна, возникающая в результате наложения двух волн, распространяющихся во взаимно противоположных направлениях и удовлетворяющих следующим условиям: частоты волн одинаковы, амплитуды являются одинаковыми функциями координат. Стоячие волны в объеме воздуха, заключенном в трубе Tр, можно получить, поместив в одном ее конце телефон Тл, а в другом микрофон-M(рис1)

Мембрана телефона порождает колебания воздуха, которые распространяются вдоль трубы в виде плоской волны. При отражении от микрофона возника­ет плоская волна противоположного направления.

В зависимости от отношений плотностей граничащих сред отражение происходит по-разному. Если среда, от которой происходит отражение, более плотная, чем среда, в которой распространяется волна, то на границе получается узел, в месте отражения волна меняет фазу на π. Отражаясь от менее плотной среды, волна не меняет фазы в месте отражения, Фазы падающей и отра­женной волн у границы одинаковы, и в этом месте получается пучность в ре­зультате сложения колебаний одинаковых фаз.

Пусть мембрана телефона совершает гармонические колебания с ампли­тудой А и циклической частотой . Тогда смещение мембраны Т в любой момент времениt представится в виде:

ξ = A Sin ωt

В волне, распространяющейся от телефона, смещение частиц воздуха в любом сечении столба, отстоящем от источника колебаний на расстоянии x (рис.1а), равно

где v - скорость распространения волны. В том же сечении в отраженной волне

смещения

где ℓ - расстояние между телефоном и микрофоном, т.е. длина воздушного столба в трубе. Знак минус учитывает изменение фазы на π при отражении. Уравнение стоячей волны смещений запишется в виде:

Амплитуда стоячей волны смещений:

изменяется от сечения к сечению по закону синуса. Сечения, в которых В=0,

называются узлами смещений. Посередине между узлами амплитуда максимальна –

это пучности смещений. Конец воздушного столба (х = 1)являетсяузлом. Графическое распределение (один из возможных случаев) амплитудных смещений В. в стоячей волне представлено на (рис. 1б.)

Фазы колебаний всех частиц, расположенных между двумя соседними узлами, одинаковы, т.е. колебания таких частиц являются синфазными. При переходе через узел фаза скачком изменяется на π , т.е. частицы расположен­ные по разные стороны узла, колеблются в противофазе.

Расстояние между двумя соседними узлами (или пучностями) называется длиной стоячей волны λ_с (рис. 1б.)

Стоячая волна деформаций 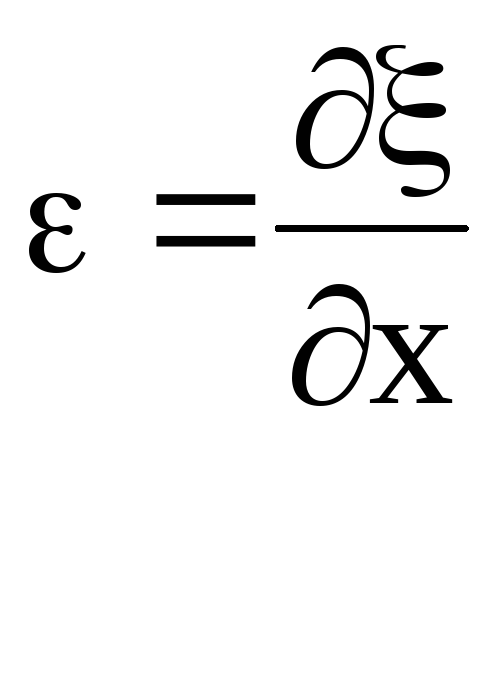(рис. 1в) сдвинута по фазе напо отношению к стоячей волне смещений В. Поэтому в узлах стоячей волны смещений скорости частиц среды равен нулю, а в её пучностях отсутствует деформации. Из этого следует, что энергия стоячей волны, заключенная между узлом и соседней пучностью локализована в этом участке среды и не переносится волной. Она только переходит из кинетической в потенциальную и обратно (дважды за период).

Звуковая волна, распространяющаяся вдоль трубы, испытывает многократное отражение от границ. Звуковые колебания в трубе являются наложе­нием всех отраженных волн и, вообще говоря, очень сложны. Картина упро­щается, если на длине L воздушного столба укладывается целое число стоячих волн или целое число бегущих волн.

где n=1,2,3… .

Частоту собственных колебаний воздушного столба в трубе можно представить в виде:

При n=1 частота соответствующего собственного колебания называется основной, все остальные собственные частоты называются обертонами (рис 2.)

Если частота источника звука (телефона) совпадает с одной из собственных частот воздушного столба, то столб воздуха, будет колебаться на этой частоте с максимальной амплитудой - возникает резонанс.

Длину столба воздуха, резонирующего на частоте источника звука, удобно находить путем плавного изменения длины воздушного столба, пере­мещая внутри трубы микрофон. О наступлении резонанса свидетельствует резкое увеличение громкости звука. При достаточно длинной трубе для заданной частоты можно найти несколько длин воздушного столба, при кото­рых наступает резонанс.

Таким образом, расстояние между двумя соседними положениями мик­рофона, соответствующее двум последовательным наступлениям резонанса (при данной частоте источника звука) равно расстоянию между двумя сосед­ними узлами скоростей (смещений) стоячей волны в трубе, т.е. половине дли­ны бегущей волны.

Так как V= λν , то, зная частоту источника звука и длину стоячей волны, можно

вычислить скорость звука.

Цели работы: Изучить свойства стоячих волн. Измерить скорость звука в воздухе. Определить вид термодинамического изопроцесса в воздухе при звуковых колебаниях.

Принадлежности: труба с телефоном и подвижным микрофоном, звуко­вой генератор, осциллограф.