Матрица эксперимента имеет вид:

увеличить

номер опыта									y(Rz)
1	+	-	-	-	+	+	+	-	2,16
2	+	+	-	-	-	-	+	+	2,65
3	+	-	+	-	-	+	-	+	3,80
4	+	+	+	-	+	-	-	-	4,70
5	+	-	-	+	+	-	-	+	2,22
6	+	+	-	+	-	+	-	-	2,48
7	+	-	+	+	-	-	+	-	4,20
8	+	+	+	+	+	+	+	+	4,89

В результате расчетов были получены следующие значения ко­эффициентов:

b₀ = 3,3875; b₁ = 0,2925; b₂=1,01; b₃ = 0,06; b₁₂ = 0,105;

b₁₃ = - 0,055; b₂₃ = 0,0875; b₁₂₃ = 0,0025

После подстановки значений коэффициентов уравнение (92) приняло вид

y=3,3375 + 0,2925x₁+1,01x₂ + 0,06x₃ + 0,105 x₁ x₁₂-0,055 x₁ x₃+0,0875x₂ x₃ + 0,0025x₁x₂x₃. (93)

Для проверки адекватности полученного уравнения и определе­ния дисперсий коэффициентов необходимо знать дисперсию воспроизводимости эксперимента S_у². Находим ее по результатам шес­ти опытов, поставленных в центре плана (опыты 1—6, табл. 34).

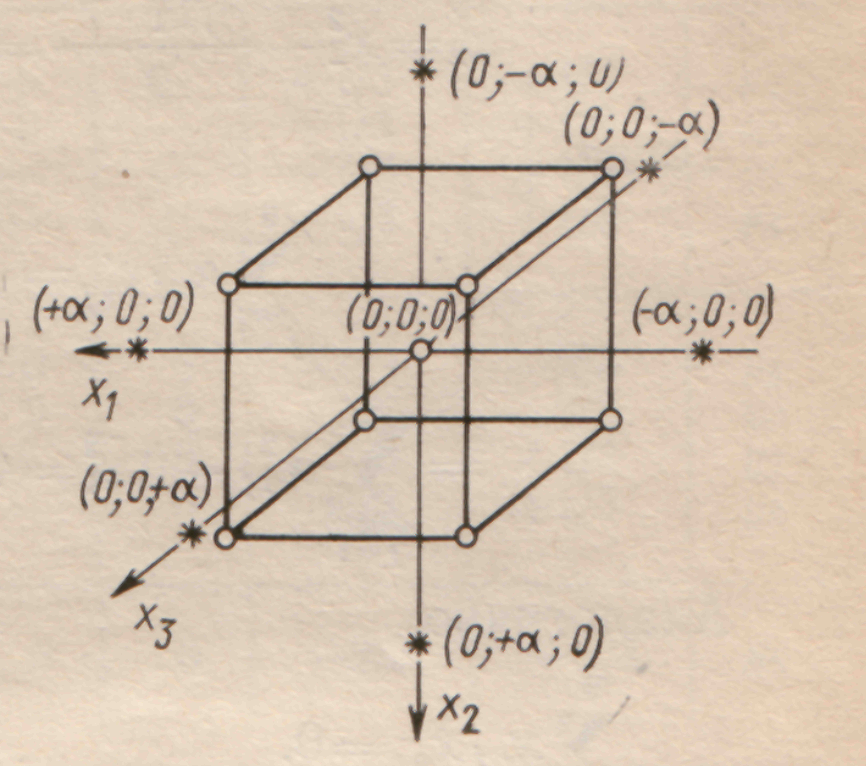
Рис. Схема центрального композиционного плана для трёх факторов

Таблица 34. Результаты опытов в центре плана и в «звездных» точках

Содержание плана	Номер опыта								y
Опыты в центре плана	1 2 3 4 5 6	+ + + + + +	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0	2,31 2,08 2,12 2,32 2,36 2,12
Опыты в «звёздных» точках	7 8 9 10 11 12	+ + + + + +	-1,682 +1,682 0 0 0 0	0 0 -1,682 +1,682 0 0	0 0 0 0 -1,682 +1,682	2,828 2,828 0 0 0 0	0 0 2,828 2,828 0 0	0 0 0 0 2,828 2,828	3,55 4,50 1,80 5,15 2,32 2,56

Среднее арифметическое значение параметра оптимизации в центре плана

Дисперсия S_У² воспроизводимости эксперимента

Разность между значением параметра оптимизации в центре плана и величиной свободного члена b₀ (напомним, что в центре плана значения всех ко

Полученная разность во много раз превышает ошибку S_y экс­перимента:

Из этого следует, что коэффициенты при квадратичных членах значимо отличаются от нуля, а исследуемая зависимость не может быть с достаточной точностью аппроксимирована уравнением (92). Поэтому перешли к планированию второго порядка и аппроксими­ровали неизвестную функцию отклика полиномом вида

(94)

Эксперимент был поставлен по программе центрального компо­зиционного ротатабельного планирования второго порядка. Реали­зованные восемь опытов полного факторного эксперимента 2³ (см. табл. 33) и шесть опытов в центре плана (см. табл. 34) дополнили шестью опытами в «звездных» точках (опыты 7—12, табл. 34). Ве­личина «звездного» плеча в рассматриваемом случае равна 1,682. Коэффициенты уравнения (94) находили по формулам (77), (78), (79), (80). Вписать эти формулы

Получили следующие значения коэффициентов:

b₀ = 2,1956; b₁ = 0,2882; b₂=0,9819; b₃ = 0,0646; b₁₂ = 0,105; b₁₃= -0,055; b₂₃=0,0875; b₁₂₃=0,0025; b₁₁ = 0,6663; b₂₂ = 0,4594; b₃₃= 0,0833.

После подстановки значений коэффициентов в уравнение (94) оно получило вид

y= 2,1956 + 0,2882х₁ + 0,9819х₂ + 0,0646х₃ + 0,105х₁х₂ - 0,055х₁х₃ +

+0,0875 х₂х₃+ 0,0025х₁х₂ х₃+0,6663 + 0,4594+0,083 (95)

Дисперсии коэффициентов, вычисленные по формулам (81), (82), (83), (84), имели следующие значения:

S²{ b₀} = 0,00258; S²{ b_i} = 0,001131; S²{b_il} = 0,00193; S²{ b_ij} = 0,00107.

Доверительные интервалы для коэффициентов равны:

Db₀ = tS{ b₀}= 2,57·0,0508= 0,1305; Db_i = tS{ b_i} = 0,0864;

Db_il = tS{ b_il}= ±0,1129; Db_ij = tS{ b_ij}= ± 0,08407.

В связи с тем что коэффициенты b₃ , b₁₂ , b₁₃ , b₂₃ , b₁₂₃ ,b₃₃ по абсолютной величине меньше соответствующих доверитель­ных интервалов, их можно признать статистически незначимыми и исключить из уравнения регрессии. Так как среди незначимых ока­зался и коэффициент b₃₃ при квадратичном члене, значимые коэф­фициенты были пересчитаны с использованием метода наименьших квадратов. Пересчитанные значения коэффициентов оказались сле­дующими:

b₀ = 2,26; b₁₁= 0,6555; b₂₂ = 0,4389; b₁=0,2882; b₂ = 0,9819

Таким образом, математическая модель, полученная в резуль­тате ротатабельного планирования второго порядка, приняла вид

у = 2,26 + 0,2882 + 0,9819+ 0,6555+0,438. (96)

Для проверки адекватности модели (96) нашли дисперсию S_ад² адекватности по формуле

Остаточная сумма квадратов

Сумма квадратов S_Е, найденная по выражению (85) и использо­ванная для определения дисперсии параметра оптимизации, равна 0,077284. При указанных значениях S_R и S_Е дисперсия S²_ад = 0,0333.

Определили расчетное значение F-критерия:

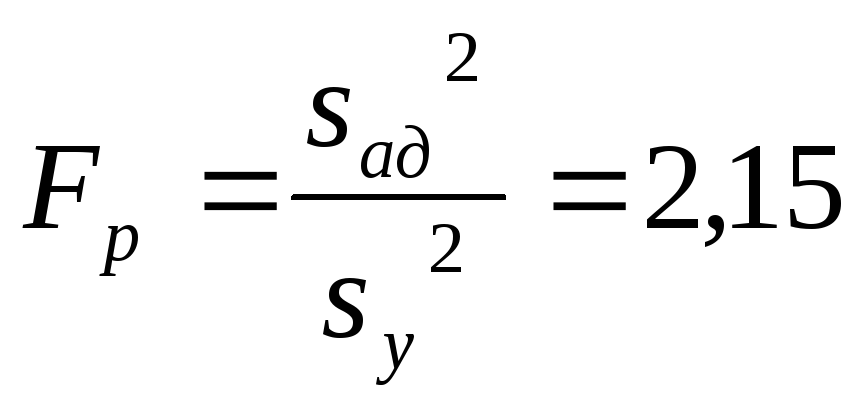
При 5%-ном уровне значимости и числах степеней свободы для числителя 10 и знаменателя 5 табличное значение критерия F_т равно 4,74. Значение F_Р<F_т, поэтому модель (96) следует признать адекватной. Уравнение (96) неудобно для интерпретации получен­ных результатов и практических расчетов, поэтому его преобразо­вали по формулам перехода от кодированных значений (х_{1 ,} х_{2 ,} х₃) к натуральным значениям факторов (u,s,t):

Где натуральные значения факторов на основных уров­нях; значения интервалов варьирования.

Таким образом,

Уравнение (96) с учетом отношений (97) можно представить следующим выражением:

(98)

Из приведенного выражения следует, что в области эксперимен­та (t = 0,250,75 мм) глубина резания не оказывает влияния на шероховатость обработанной поверхности капролона. Уравнение (96) используем для поиска оптимального режима обработки кап­ролона резцом с заданной геометрией. В результате переноса на­чала координат в центр фигуры с координатами х_1s=-0,22; х_2s = = -1,12 (они соответствуют значениям u=181 м/мин; s= 0,276 мм/об) и поворота координатных осей уравнение (96) было приведено к каноническому виду

Y - 1,68 = 0,6555 + 0.4389. (99)

Выражение (99) является уравнением эллипса в каноническом виде. Так как коэффициенты B₁₁ и B₂₂ имеют положительные знаки, центр эллипсов

(х_1s =-0,22; х_2s = -1,12) является минимумом функции отклика. В этом случае для поиска экстремума достаточ­но поставить опыт в центре фигуры и проверить, насколько точно значение параметра оптимизации, предсказанное уравнением рег­рессии, совпадает с экспериментальным.

В дополнительном опыте, поставленном в центре фигуры (х_1s = -0,22;

х_2s = -1,12), получено значение функции отклика у = = 1,7 мкм. Дальнейшее варьирование скорости и подачи вблизи экстремума не вызвало уменьшения значения y. Таким образом, оптимальным следует считать режим: у = 181 м/мин, s= 0,276 мм/об при t= 0,250,75 мм.

Уравнение (99) можно также использовать для определения ожидаемой шероховатости поверхности при об­работке капролона на режимах, входящих в область эксперимента.