2. Графы и матрицы как средство структурного анализа хтс

Удобным средством описания структуры ХТС являются графы и матрицы.

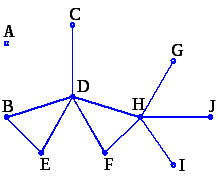
Граф представляет геометрическое изображение, состоящее из ряда ребер и вершин (рис. 2.1). Вершины графа символизируют объекты, а ребра – отношения связи между ними. Отношения могут быть симметричными и ассиметричными. Отношение называется асимметричным, если между вершинами а и b оно существует, а между b и а – нет. Например, асимметричным будет отношение: диаметр корпуса аппарата Da меньше, чем диаметр рубашки Dp (Da < Dp). Для выражения асимметрии ребру придается ориентация. Ориентированное ребро обычно называют дугой. Дуга изображается в виде стрелки, направленной от подлежащего к дополнению. Граф, в котором задана ориентация ребер, называется ориентированным графом (рис. 2.2).

Рис. 2. 1. Граф	Рис. 2. 2. Ориентированный граф

В математике граф рассматривается как нечто абстрактное. Мы же будем вкладывать в понятия «ребро» и «вершина» смысловую нагрузку, получая при этом инструмент для описания конструктивной схемы аппарата или ХТС. Например, вершины A,B,C,Gи т.д. представляют элементы конструкции аппарата, а ребра (дуги)CD,BD,DHи другие – связь между ними.

Использование графов при геометрическом моделировании технологического оборудования

Свойства графов

Маршрут – последовательность ребер, образующих непрерывный путь между исходной и конечной вершинами. Для графа, описывающего конструктивную схему аппарата, последовательность ребер устанавливает взаимосвязь между отдельными элементами конструкции.

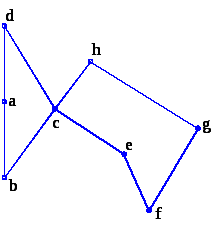
Цикл – последовательность ребер, в которой исходная и конечная вершины совпадают. Например (рис. 2.3), последовательность gfechg является циклом, так как она берет начало из одной вершины g (точки g) и заканчивается в ней.

Маршрут ориентированного графа (рис. 2.4). Особенностью маршрута ориентированных графов является то, что можно перемещаться только в соответствии с указанием стрелки. Так, маршрут acdged существует, а acde – нет, т.к. дуги de не существует, а есть только дуга ed.

Рис. 2. 3. Цикл неориентированного графа	Рис. 2. 4. Цикл ориентированного графа

Существует несколько последовательностей дуг между вершинами аиb.При определении таких последовательностей важно установить направления дуг.

Петлей называется последовательность дуг, в которой исходная и конечная вершины совпадают. Петли в ориентированном графе эквивалентны циклу. Петля считается определенной лишь тогда, когда она, выйдя из начальной вершины и, пройдя через различные промежуточные вершины в указанном стрелками направлении, возвратится на исходную позицию. Отметим, что ориентированные графы могут содержать циклы, определяемые после удаления направленности из графа. Из четырех циклов, представленных на рисунке, только три являются петлями. Действительно, вершину h можно покинуть двумя путями, но нет пути, по которому можно было бы в нее вернуться.

Геометрия графов. Граф представляет собой геометрическую фигуру, но принципы, которыми руководствуются при ее построении, отличаются от принципов, используемых в геометрии. Он не рассматривается в виде жесткой конструкции в своей плоскости, как это имеет место при составлении конструктивной схемы аппарата или его эскиза. Более того, отрезки, соединяющие вершины, не обязательно должны быть линиями определенного вида (прямыми, окружностями и т.д.).

На рис. 2.5. первые три графа графически эквивалентны: каждый содержит три вершины и три соединяющие их в одной и той же последовательности дуги. Их эквивалентность не зависит от того, как изображены дуги – прямыми, круговыми или волнистыми линиями. Третий и четвертый ориентированные графы не являются эквивалентными по теории графов т.к. в одном из них можно продвигаться по петле в обратную сторону, а в другом нельзя.

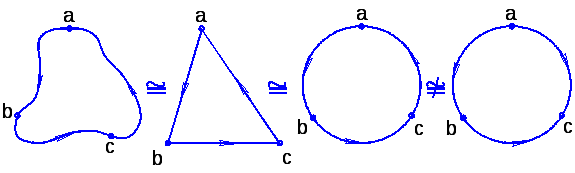
Рис. 2. 5. Геометрия графов

Связность. Важным свойством графов является их связность. Говорят, что неориентированный граф связан, если существует, хотя бы один путь между каждой парой вершин. В свою очередь, ориентированный граф связан, если неориентированный граф, полученный из первого удалением ориентации дуг, является связанным. Это свойство графов имеет большое значение для описания конструктивных схем аппаратов, так как связность графов следует из самой природы описываемого объекта (аппарата, ХТС).

Планарность. Граф называется планарным, если он может быть начерчен на плоскости таким образом, чтобы произвольные две дуги графа не пересекались, друг с другом. Классическими непланарными графами являются те, у которых каждая из вершин соединена со всеми другими, т. е. полные графы (рис. 2.6). В большинстве случаев свойство планарности характерно для графов конструктивных схем аппаратов, хотя в настоящее время нельзя достоверно утверждать, должен ли граф конструктивной схемы быть обязательно планарным.

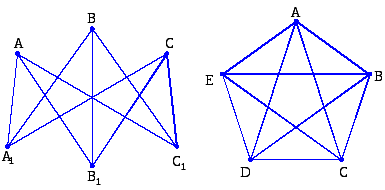
Рис. 2.6. Непланарные графы

Дерево – разновидность графа. Дерево представляет собой граф, не содержащий циклов (рис.2.7), что упрощает его структуру и делает планарным. Это связный граф, так как каждая вершина в нем завершает, по крайней мере, одно его ребро, и не существует вершин, которые не завершали бы ребро.

Рис. 2. 7. Древовидный граф: а – неориентированные и б – ориентированный графы древовидной структуры

Графы древовидной структуры наиболее хорошо подходят для описания иерархических систем. Иерархическими называются системы, имеющие многоуровневую структуру. Такие системы весьма разнообразны и встречаются в различных областях деятельности человека, природе, технике.

Способы представления графов

Наиболее простым и наглядным способом представления графа на бумаге является геометрическое изображение точек и линий, что неприемлемо в случае обработки информации с помощью ЭВМ. Для ЭВМ граф представляют дискретным способом в виде матриц. Рассмотрим несколько используемых типов матриц.

Матрица смежности. Матрица смежности обозначается через |А|=[а_ij] и определяется следующим образом:

а_ij = 1, если в графе существует дуга (Xi, Xj);

а_ij = 0, если в графе нет дуги (Xi, Xj).

Матрица смежности графа, рассмотренного нами на рис. 2.2 имеет следующий вид (здесь и далее значение «0» в клетку не проставляется):

	A	B	C	D	E	G	F	I	H	J
A
B				1	1
C				1
D							1
E				1
G									1
F									1
I									1
H				1				1
J									1

Матрица смежности полностью определяет структуру ориен­тированного графа. Вершина Aв рассматриваемом графе является изолированной, и для нее как столбец, так и строка содержат только нули.

Для неориентированного графа число элементов в матрице смежности возрастает в два раза, однако, она становится симметричной относительно диагонали. В результате экономится почти 50% объема памяти вычислительной машины при их анализе.

	A	B	C	D	E	G	F	I	H	J
A
B				1	1
C				1
D		1	1		1		1		1
E		1		1
G									1
F				1					1
I									1
H				1		1	1	1		1
J									1

Матрица инциденций. Матрица инциденций обозначается через |В|=[b_ij], имеет размерность п х m иопределяется следующим образом (п– количество вершин,m– количество дуг):

b_ij = 1, если Х_i является начальной вершиной дуги а_j;

b_ij = -1, если X_i является конечной вершиной дуги а_j;

b_ij = 0, если Х_i не является концевой вершиной дуги а_j, или если а_j,является петлей.

Для графа, приведенного на рис. 2.2 матрица инциден­ций имеет вид

	а1	а2	а3	а4	а5	а6	а7	а8	а9	а10
A
B	1	1
C				1
D	-1		-1	-1	-1					1
E		-1	1
G						1
F							1			-1
I									-1
H					1	-1	-1	-1	1
J								1

Поскольку каждая дуга инцидентна двум различным вершинам, за исключением случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент, равный 1, и один, равный -1, либо все элементы столбца равны 0. Если граф является неориентированным графом, то его матрица инциденций определяется так же, как и выше, при этом все элементы, равные -1, заменяются на +1.

Матрица весов. Граф, в котором каждому ребру а_ij, поставлено некоторое число w_ij, называется взвешенным графом, а число w_ij, – весом ребра а_ij. В графах конструктивных схем аппаратов эти веса могут представлять некоторые физические величины, такие, как линейные размеры отдельных элементов или их веса. Простой взвешенный граф может быть представлен своей матрицей весов |W|= [w_ij], где w_ij есть вес ребра, соединяющего вершины i и j. Веса несуществующих ребер обычно полагают равными 0, и матрица весов является простым обобщением матрицы смежности.