2. В двух цехах а и в одного завода собирается два вида продук­ции мотопилы и сепараторы.

Допустимое время работы цеха А — 150 часов в месяц, цеха В — 160 часов в месяц. На сборку мотопилы требуется 10 часов в цехе А и 20 часов в цехе В. Для сборки сепаратора — 15 часов и 10 часов соответственно. Необходимо, в соответствии с требованиями, осуществить проверку качества. Каждая мотопила должна быть испытана в тече­ние 30 часов, сепаратор — в течение 10 часов, но все вместе не менее чем в течение 135 часов. По крайней мере, общая численность продуктов мотопил и сепараторов должна быть не менее 5. Каков должен быть план работы цехов А и В, чтобы прибыль была максимальной, если издержки и доход от одной мотопилы составляют $2 000 и $3 000 соответственно, а от одного сепаратора— $ I 500 и $2 500 соответственно и на одну мотопилу должно приходиться не менее 3-х сепараторов?

3. Придумайте самостоятельно проблему, которую можно пред­ставить как задачу ЛП.

4. От стандартного вида задачи ЛП вы перешли к каноническому. Чему стало равно число переменных?

2.6.3. Геометрическая интерпретация решения задач ЛП

Если задача ЛП является задачей с двумя неизвестными х₁ и х₂, то можно применить для ее исследования так называемый графичес­кий способ, основанный на геометрической интерпретации задачи ЛП.

Ограничения задачи ЛП определяют некоторую область в первой четверти плоскости x_l0x₂. Чтобы построить эту область (область пла­нов задачи ЛП) необходимо графически решить систему неравенств, представляющих собой ограничения. Для этого изобразим область допустимых решений задач ЛП.

Известно, что любое линейное неравенство с двумя переменны­ми делит плоскость на две полуплоскости, точки одной из которых удовлетворяют данному неравенству, точки другой — не удовлетворяют. Границей этих полуплоскостей является прямая, в уравнении кото­рой левые и правые части такие же, как и в данном неравенстве. На­пример, изобразим графически неравенство

Алгоритм построения

1. Строится прямая

2. Все точки, лежащие выше прямой, удовлетво­ряют данному неравенству. Для этого достаточно взять какую-нибудь точку из любой полуплоскости и проверить, удовлетворяют или нет ее координаты данному неравенству. Самое простое — взять точку 0(0, 0), .

Следовательно, выбранная точка принадлежит мно­жеству точек, удовлетворяющих данному неравенству. Если неравенство нестрогое, то точки прямой также будут удовлетворять неравенству.

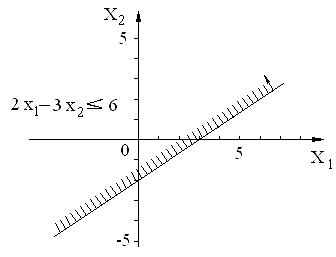
Рис. 2.13. Графическое изображение неравенства .

Теперь ясно, как изобразить графически систему неравенств. Необходимо графически изобразить каждое неравенство, пересечение (об­щая часть) решений всех неравенств и будет изображать искомую область. Например, изобразим графически систему неравенств:

,

, (2,39)

,

Необходимо рассматривать только первую четверть, т. к. х₁ и х₂ неотрицательны.

Решением данной системы является многоугольник, вершины которого находятся в точках (0, 0), (0, 10), (5, 8), (9, 4), (11, 0). Вершины многоугольника, являющегося решением данной системы неравенств определяются попарным решением линейных уравнений системы (2.39). Если данные неравенства суть ограничения задачи ЛП, то любая точка из получен­ного многоугольника (включая его границы) будет являться планом задачи ЛП (рис. 2.14).

Рис. 2. 14 Ограниченный план задачи ЛП

Рассмотрим еще один пример. Изобразим графически решение следующей системы неравенств:

,

, (2.40)

,

Чем отличаются решения систем неравенств (2.39) и (2.40)? В первом случае получен многоугольник, т.е. ограниченное мно­жество; во втором область оказалась неограниченной (рис. 2.15). Итак, области планов задач ЛП могут быть как ограниченными, так и неограничен­ными.

Рис. 2.15 Неограниченный план задачи ЛП

А как поступать в случае, когда система неравенств в ограничени­ях задачи ЛП изображается, например, в виде двух областей?

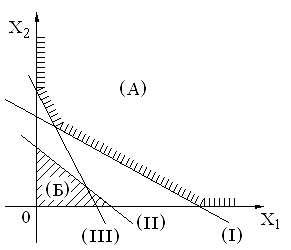
Рис. 2.16 Несовместная область планов задачи ЛП.

Этот случай соответствует тому, что задача ЛП сформу­лирована неправильно, т. к. различные условия (рис. 2.16) области А и Б противоре­чивы. Этот случай называется несовместной задачей ЛП.

Теперь перейдем к графическому изображению целевой функции

Z = С₁х₁ + С₂х₂.

Если величина Z будет принимать различные значе­ния Z₁, Z₂ ... , то очевидно, что целевая функция может быть изобра­жена в виде параллельных между собой прямых. Например, возьмем Z = 3x₁ + 2x₂. Придавая Z различные значения, изобразим прямые, соответствующие Z₁ =0, Z₂ = 6, Z₃=12.

Рис. 2.17. Изображение целевой функции.

Все эти прямые перпендикулярны вектору с координатами (3, 2) (Почему?). В общем случае: параллельные прямые, изображающие гра­фически целевую функцию Z = С₁х₁ + С₂х₂ при различных ее значе­ниях, перпендикулярны вектору С с координатами (С₁, С₂). Если пря­мую передвигать по направлению вектора С параллельно самой себе, будут получены прямые, координаты которых увеличивают значение целевой функции.

Введем следующие определения: прямая, имеющая общие точки с многоугольником и лежащая по одну сторону от него, называется опорной прямой.

Соответственно: план задачи ЛП, принадлежащий опорной прямой и находящийся в вершине многоугольника, называется опорным планом.

Теперь становится ясным, как графически найти решение задачи ЛП, т.е. из множества точек, являющихся планами задачи ЛП, выб­рать оптимальный план. Для этого необходимо:

1) построить область планов задачи ЛП;

2) построить прямую, соответствующую какому-нибудь значению целевой функции, например С₁х₁ + С₂х₂ = 0;

3) перемещать эту прямую параллельно самой себе до соприкосновения с областью допустимых планов задачи ЛП.

4) в случае решения задачи на максимум (минимум) эту прямую переме­щать в направлении вектора C (C₁,C₂) (противоположном), пока она не станет опорной. Точка опорной прямой, одновременно принадлежащая области допустимых планов, будет оптимальным решением.

Замечание. Этапы 2 и 3 можно объединить, т.е. сразу строить прямую, соответствующую какому-то зна­чению целевой функции, которая бы имела об­щие точки с областью допустимых планов.

Примеры: Рассмотрим следующую зада­чу ЛП:

,

,

, (2.41)

,

1. Строим область планов задачи:

2) Строим прямую

Рис 2.18 План задачи (2.41) и построение прямой, соответствующей целевой функции.

3) Передвигаем параллельно прямую по направле­нию вектора С (2,5). Координаты точки В являются решением задачи.

рис 2.19. Графическое нахождение решения задачи ЛП

Если перемещать прямую А дальше, то значение целевой функции будет возрастать. Точка В является оптимальным планом дан­ной задачи и именно в ней целевая функция принимает наименьшее значение.

Отметим следующий факт. Если при данных ограничениях искать максимум функции Z, то найти его невозможно, т. к. область планов является неограниченной и целевая функция при дви­жении прямой А по направлению вектора С неограниченно будет воз­растать.

Рассмотрим случай задачи на максимум:

,

, (2.42)

,

Изобразим область допустимых решений (треугольник ABC) и прямую (D), соответствующую нулевому значению целевой функ­ции, т. е. (рис. 2.20)

Рис. 2.20 Область решений представляет треугольник .

Прямая D не имеет общих точек с треугольником ABC Поэтому передвигаем прямую D в направлении обратном вектору С параллельно самой себе, построим две опорные пря­мые Е и F.

Увеличение значения целевой функции происходит в направле­нии вектора (2; -5), следовательно, значение функции Z в точках пря­мой Е больше, чем в точках прямой F. В данном случае максимум целевой функции находится в точке В (в точке С— минимум). Очевид­но, что значения Z в любых других точках треугольника ABC меньше, чем в точке В и больше, чем в точке С.

Определив графически точки, в которых целевая функция имеет минимум (или максимум), можно найти координаты этих точек. Для этого надо решить систему из двух уравнений с двумя неизвестными x₁, x₂. Эти уравнения определяются прямыми, на пересечении кото­рых находится точка, являющаяся оптимальным планом.

В частности, в задаче (2.41) координаты точки В определяются из системы уравнений:

;

.

Решение имеет вид

Тогда:

В задаче (2.42) координаты В определяются из системы

;

Ее решение

;

.

Из приведенных примеров интуитивно можно сделать вывод, что оптимальный план любой задачи ЛП находится в точке, являю­щейся одной из вершин множества допустимых решений. Такие точ­ки называются угловыми точками. Вопрос: а как быть в случае, когда прямая, изображающая целевую функцию, становится опорной более чем в одной точке?

Этот случай возможен только тогда, когда прямая, изображающая целевую функцию, параллельна одной из сторон многоугольника ре­шений, например, как на рисунке 2.21, приведенном ниже.

,

Здесь прямая D соответствует нулевому значению целевой функции

Рис. 2.21. Задача ЛП имеет множество решений

В этом случае максимум целевой функции определяется координатами любой точки отрезка АВ, в том числе и координатами угловых точек А и В. Это случай, когда задача ЛП имеет множество решений.

Графический способ решения задач ЛП применяется лишь в слу­чае, когда число неизвестных равно двум. В принципе, графически можно найти решения и для случая п = 3, но при этом необходимо строить плоскости в системе трех координат, наглядно изображать объемные картины. Во всех остальных случаях графический способ не применим.

Аналитически задача ЛП решается симплекс-методом, который заключается в алгебраическом переборе угловых точек области решений в направлении улучшения целевой функции.

Пример. Задача об оптимальном плане выпуска стульев [21]

Суть задачи. Мебельная фабрика может выпускать стулья двух типов ценою в 8 и 12 условных единиц (у.е.). Под заказ выделены материальные и людские ресурсы (таблица 2.13).

Таблица 2.13

Стул	Расход досок, м	Расход ткани, м2	Расход времени, чел.-час.
Первый	2	0.5	2
Второй	4	0.25	2.5
Ресурс	490	65	320

Спрашивается, как нужно спланировать производство стульев, чтобы получить изготовить их либо количеством, либо ценой поболее. Это и отображено в отчете о решении задачи на рис. 2.22.

Рис. 2.22. Пример решения задачи ЛП в MathCAd

Примечание: количество стульев должно быть целым.

2.7 Транспортная задача

2.7.1. Постановка транспортной задачи на примере

Некоторая компания имеет 4 завода, расположенных в разных пунктах (обозначим А, В, С, D). Необходимое сырье для выпуска продукции компания содержит на 3-х разных складах (обозначим 1, 2, 3). Известно, какое количество сырья требуется каждому заводу, например, в течение месяца: заводу А необходимо 400 т, В — 900 т, С — 200 т, D — 500 т. Всего нужно 2000 т. Также известно, что на первом складе находится 500 т сырья, на втором — 700 т, па третьем — 800 т, т. е. общее количество — 2000 т. И, наконец, существует информация о стоимости перевозки 1т сырья с любого склада на любой завод. Эти данные наглядно можно изобразить в виде матрицы затрат (таблицы):

Таблица 2.14

Склады	Заводы
	A	B	C	D
I	12	13	4	6
II	6	4	10	11
III	10	9	12	4

Каждый элемент матрицы показывает стоимость перевозки одной тонны с соответствующего склада (строка матрицы) на конкретный завод (столбец матрицы). Так, например, число 10, стоящее во второй строке и в третьем столбце, показывает, что перевозка одной тонны со второго склада на завод С обойдется компании в $10. Так как запасов сырья столько же, сколько требуется заводам, то можно удовлетворить все потребности и, очевидно, существует много способов, откуда, как и куда доставить это сырье.

Цель решения задачи: осуществление всех перевозок с наименьшей общей стоимостью. Можно потратить много времени, перебрав все возможные варианты, а можно и использовать научный подход.

Сформулируем данную проблему на языке математики. Рассматриваемая реальная ситуация очень напоминает конкретные ситуации, которые сводились к задачам ЛП.

Прежде всего нужно ввести переменные задачи. Обозначим через х_ij — количество сырья, которое перевозится из i — ого склада на j — ый завод. В нашем случае i = 1,2, 3; j = А, В, С, D. Так, например, x_2B — это количество тонн сырья, перевозимое со второго склада на завод В.

Подсчитаем стоимость перевозки всего сырья, например, с первого склада:

Аналогичным способом вычисляется стоимость перевозок и для других складов. Теперь ясно, как подсчитать стоимость всех перевозок, которую обозначим через Z

(2.48)

Функция Z есть не что иное, как целевая функция, которую нужно минимизировать и она линейная.

Перейдем к ограничениям. По условиям задачи известно, что с каждого склада должно быть вывезено все сырье. Это значит, что сумма всех х_ij (для каждой i — той строки) должна быть равной количеству сырья, находящемуся на i — ом складе, т.е.

(2.49)

Кроме того, известно, что на каждый завод должно быть завезено определенное количество сырья, т.е.

(2.50)

Имеется 3+4 = 7 ограничений и 3•4 = 12 переменных. Необходимо также учесть тот факт, что все х_ij не могут быть отрицательными. Таким образом, исходная проблема может быть сформулирована в форме задачи линейного программирования:

Найти такие неотрицательные значения переменных х_ij , которые

минимизировали бы функцию (2.48) и удовлетворяли бы

ограничениям (2.49) и (2.50).

Данная задача носит название транспортной задачи.