
- •4. Электромагнитные колебания и волны
- •4.1. Колебательный контур
- •4.2. Колебательный контур с затуханием
- •4.3. Вынужденные колебания в lcr-контуре
- •4.4. Переменный ток в электрических цепях
- •4.4.1. Активное, индуктивное и емкостное сопротивления
- •4.4.2. Закон Ома для переменного тока. Активное и реактивное сопротивления
- •4.4.3. Метод векторных диаграмм
- •4.4.4. Эффективные напряжение и ток
- •4.4.5. Мощность в цепи переменного тока
- •4.5. Электромагнитные волны
- •4.5.1. Шкала электромагнитных волн
- •4.5.2. Получение электромагнитных волн
- •4.5.3. Энергия электромагнитных волн. Вектор Умова-Пойнтинга
- •Список литературы
4.3. Вынужденные колебания в lcr-контуре
![]() .
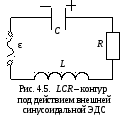
Это можно с помощью воздействия на
контур внешней периодической
электродвижущей силы (рис. 4.5). При этом
в контуре возникнут вынужденные
колебания. Будем рассматривать
синусоидальную ЭДС, т.е. ЭДС, зависящую
от времени по закону синуса (или косинуса):
.
Это можно с помощью воздействия на
контур внешней периодической
электродвижущей силы (рис. 4.5). При этом
в контуре возникнут вынужденные
колебания. Будем рассматривать
синусоидальную ЭДС, т.е. ЭДС, зависящую
от времени по закону синуса (или косинуса):
![]() ,
,
где
![]() циклическая частота
колебаний ЭДС.
циклическая частота
колебаний ЭДС.
Согласно второму правилу Кирхгофа сумма падений напряжений на отдельных элементах контура равна внешней ЭДС:
![]()
![]()
![]()
![]()
![]() .
.
Обозначая
![]() и учитывая, что
и учитывая, что![]() ,
,![]() ,
получим
,
получим
![]() .
(4.18)
.
(4.18)
Уравнение (4.18) называется дифференциальным уравнением вынужденных колебаний под действием синусоидальной ЭДС.
С точки зрения математики уравнение (4.18) представляет собой линейное неоднородное (правая часть отлична от нуля) дифференциальное уравнение с постоянными коэффициентами. Решение данного уравнения представляет собой сумму двух слагаемых
![]() .
.
Первое
слагаемое – общее решение однородного
уравнения (с правой частью, равной нулю),
второе слагаемое – частное решение
неоднородного уравнения. Первое слагаемое
в точности совпадает с уравнением (4.13)
и представляет собой затухающие колебания
заряда конденсатора с циклической
частотой
![]() .
Второе слагаемое соответствует
собственным вынужденным колебаниям
заряда с циклической частотой вынуждающей
силы
.
Второе слагаемое соответствует
собственным вынужденным колебаниям
заряда с циклической частотой вынуждающей
силы![]() .
Таким образом, в начальный момент времени
колебания представляют собой сумму
колебаний с частотами
.
Таким образом, в начальный момент времени
колебания представляют собой сумму
колебаний с частотами![]() и
и![]() .
Такой режим колебаний называетсяпереходным. Первое слагаемое
экспоненциально затухает за время по
порядку величины, равное времени
затухания
.
Такой режим колебаний называетсяпереходным. Первое слагаемое
экспоненциально затухает за время по
порядку величины, равное времени
затухания![]() .
Переходный режим заканчивается и
наступает режимустановившихся
вынужденных колебаний с частотой
вынуждающей силы
.
Переходный режим заканчивается и
наступает режимустановившихся
вынужденных колебаний с частотой
вынуждающей силы![]()
![]() .
(4.19)
.
(4.19)
Характеристики
вынужденных колебаний
![]() изависят, во-первых,
от параметров вынуждающей силы
изависят, во-первых,
от параметров вынуждающей силы![]() и
и![]() ,
во-вторых, от параметров самой колебательной
системы
,
во-вторых, от параметров самой колебательной
системы![]() и
и![]() ,
но не зависят от начальных условий.
Подставляя функцию
,
но не зависят от начальных условий.
Подставляя функцию![]() (4.19) в уравнение (4.18), можно найти выражение
для амплитуды вынужденных колебаний
(4.19) в уравнение (4.18), можно найти выражение
для амплитуды вынужденных колебаний![]() и величины. Опуская
математические выкладки, приведём
конечные результаты:
и величины. Опуская
математические выкладки, приведём
конечные результаты:
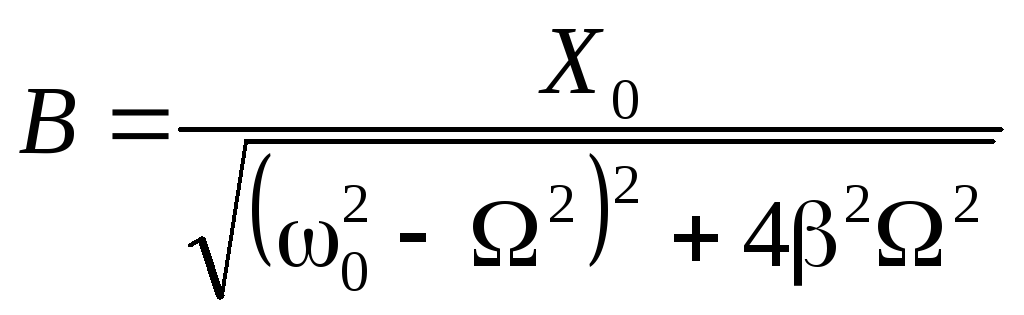 ,
(4.20)
,
(4.20)
![]() . (4.21)
. (4.21)
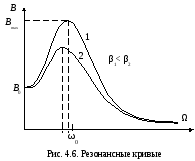
![]() (4.20), показанный на рис. 4.6, называетсярезонансной кривой. Резонансная
кривая имеет максимум. Максимальное
значение амплитуды установившихся
колебаний достигается при резонансной
частоте
(4.20), показанный на рис. 4.6, называетсярезонансной кривой. Резонансная
кривая имеет максимум. Максимальное
значение амплитуды установившихся
колебаний достигается при резонансной
частоте![]() ,
которая при небольшом затухании мало
отличается от собственной циклической
частоты колебаний системы
,
которая при небольшом затухании мало
отличается от собственной циклической
частоты колебаний системы![]() .
Таким образом, резонанс наступает при
условии совпадения частоты внешней
синусоидальной силы и собственной
частоты колебательной системы
.
Таким образом, резонанс наступает при
условии совпадения частоты внешней
синусоидальной силы и собственной
частоты колебательной системы![]() .
Кривая 1 на рис. 4.6 относится к колебательной
системе с меньшим затуханием. Чем меньше
коэффициент затухания, тем ближе
резонансная частота к собственной
частоте системы и больше значение
максимальной амплитуды, т.е. острее и
уже пик резонансной кривой. Отметим,
что ширина максимума на уровне
.
Кривая 1 на рис. 4.6 относится к колебательной
системе с меньшим затуханием. Чем меньше
коэффициент затухания, тем ближе
резонансная частота к собственной
частоте системы и больше значение
максимальной амплитуды, т.е. острее и
уже пик резонансной кривой. Отметим,
что ширина максимума на уровне![]() равна коэффициенту затухания:
равна коэффициенту затухания:![]() .
.
Пример
4.3. Вывести
формулу для величин резонансной частоты
![]() и максимальной амплитудыBmax
(рис. 4.6).
и максимальной амплитудыBmax
(рис. 4.6).
Решение. Для того
чтобы найти точку максимума
![]() резонансной кривой, нужно в соответствии
с правилами математики взять производную
функции
резонансной кривой, нужно в соответствии
с правилами математики взять производную
функции![]() (4.20) и приравнять её к нулю:
(4.20) и приравнять её к нулю:![]() .
В результате получится
.
В результате получится![]() .
.
Далее,
подставляя значение
![]() в формулу 4.20, получим
в формулу 4.20, получим![]() ,
где
,
где![]() циклическая частота
затухающих колебаний.
циклическая частота
затухающих колебаний.
Если частота
внешней силы
![]() ,
то значение амплитуды по формуле
(4.20)
,
то значение амплитуды по формуле
(4.20)![]() ,
что соответствует статическому заряду
конденсатора, приобретаемому при
подключении его кпостояннойЭДС
,
что соответствует статическому заряду
конденсатора, приобретаемому при
подключении его кпостояннойЭДС![]() .
.
Отношение резонансной амплитуды
![]() к величине статического отклонения
колебательной системы
к величине статического отклонения
колебательной системы![]() называетсядобротностью колебательной
системы
называетсядобротностью колебательной
системы![]() .
.
Используя формулы для
![]() и
и![]() (см. пример 4.3), а также связь циклической
частоты с периодом колебаний
(см. пример 4.3), а также связь циклической
частоты с периодом колебаний![]() ,
получим:
,
получим:
![]() .
.
Поскольку
![]() логарифмический
декремент затухания, то:
логарифмический
декремент затухания, то:
![]() .
(4.22)
.
(4.22)
Чем меньше декремент затухания, тем выше добротность контура, и тем более он пригоден для радиотехники.
Далее мы покажем, что добротность контура пропорциональна отношению энергии, запасённой в контуре, к её потерям за период колебаний (т.е. энергии, выделяющейся в контуре за период в виде тепла).
