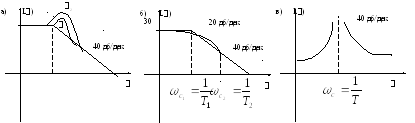- •Классификация сау по непрерывным динамическим процессам:
- •По принципу линейности динамических процессов.
- •II. Классификация по характеристикам управления. По принципу управления:
- •По принципу управляющего сигнала:
- •По поведению в установившемся режиме:
- •Классификация сау по другим признакам.
- •2,3,4 Системы статического и астатического регулирования.
- •5. Уравнение статики и динамики.
- •6. Формы записи линейных диф уравнений. Передаточные ф-ии.
- •7. Структурные схемы. Преобразование структурных схем.
- •8. Частотные характеристики.
- •Передаточная функция звена (w(p)).
- •Афх. Если параметруp придать значение j, где и в передаточной функции заменить всеp , то получим:
- •9. Временные характеристики.
- •16. Неминимально-фазовые звенья. Звено чистого запаздывания.
- •17. Основные понятия метода пространства состояний. Решения уравнения состояния линейных непрерывных систем.
- •18. Схемы переменных состояний. Метод прямого программирования.
- •23. Понятие устойчивости. Условие устойчивости линейных непрерывных систем автоматического управления. Влияние корней на устойчивость системы.
- •Геометрическая интерпретация устойчивости.
- •26. Критерий Найквиста.
- •27. Устойчивость систем со звеном запаздывания.
- •Логарифмический критерий устойчивости.
- •Запас устойчивости по алгебраическому критерию Гурвица.
- •З Im Reапас устойчивости по фазе и модулю по частотному критерию Найквиста.
- •29. Структурно устойчивые и структурно неустойчивые системы. Влияние структуры и передаточного коэффициента на устойчивость.
- •30. Оценка качества управления. Прямые показатели качества.
- •Влияние нулей передаточной функции на переходный процесс
- •Диаграмма Вышнеградского
- •36. Типовые алгоритмы управления.
- •37. Методы коррекции динамических свойств систем.
- •38. Синтез линейных систем управления.
- •40. Синтез последовательных корректирующих устройств по лачх.
- •Импульсные сау
- •44. Преимущества и недостатки дискретных систем.
- •45. Описание чисто дискретных систем, решение линейных разностных уравнений.
- •Дискретная передаточная функция.
6. Формы записи линейных диф уравнений. Передаточные ф-ии.
![]()
![]()
![]() оператор
реакции (выхода) D(p)
оператор воздействия(входа)K(p)
оператор
реакции (выхода) D(p)
оператор воздействия(входа)K(p)
![]()
Передаточная функция:
![]()
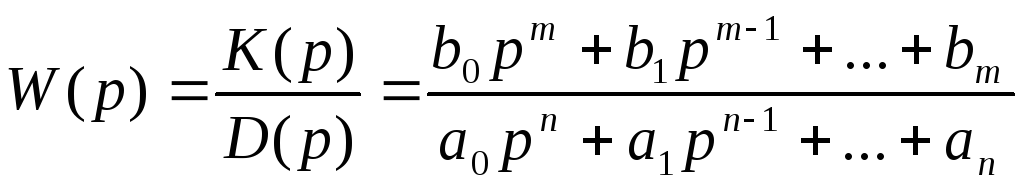
![]()
![]()
П![]() ередаточной
функцией
звена (системы) называется отношение
изображений Лапласа выходной функции
к входному воздействию при нулевых
начальных условиях
ередаточной
функцией
звена (системы) называется отношение
изображений Лапласа выходной функции
к входному воздействию при нулевых
начальных условиях
Знаменатель передаточной функции называют характеристическим полиномом, а, приравняв знаменатель к нулю, получим характеристическое уравнение. Корни знаменателя называются полюсами, а корни числителя – нулями. Передаточная функция зависит от конструкции устройства и свойств материала конструкции, но не зависит от входных воздействий и выходной функции. Переходной функцией называется реакция системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.
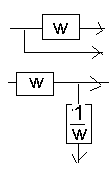
7. Структурные схемы. Преобразование структурных схем.
1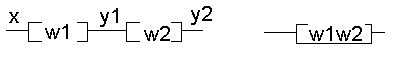 )
)
y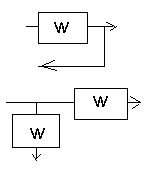 1=xw1
y2=xw1w2
1=xw1
y2=xw1w2
2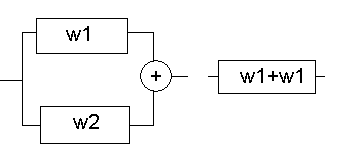 )
3)
)
3)
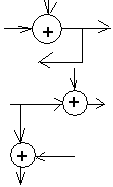
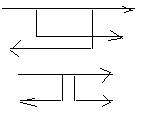
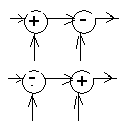
4) 5) 6) 7)
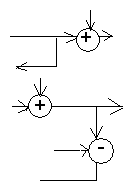
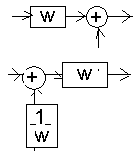
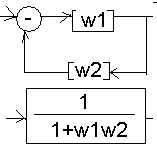
8) 9) 10)
8. Частотные характеристики.
Частотными называются характеристики звеньев (систем) в форме графиков или таблиц, отображающие изменение амплитуды и фазы выходной функции (т.е. реакцию) звеньев или систем относительно синусоидального входного воздействия в установившемся режиме при изменении частоты от 0 до . Очевидно, что при экспериментальном определении частотных характеристик диапазон изменения частоты входного гармонического воздействия ограничен техническими возможностями аппаратуры. Для линейных систем справедлив ПРИНЦИП СУПЕРПОЗИЦИИ, который можно сформулировать следующим образом.
|
Реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. |
Это позволяет ограничиться изучением систем только с одним входом.
Передаточная функция звена (W(p)).
Амплитудно-фазовая характеристика (АФХ).
Амплитудно-частотная характеристика (АЧХ).
Фазо-частотная характеристика (ФЧХ).
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
Передаточная функция звена (w(p)).
Э![]() то
отношение прямого преобразования
Лапласа сигнала на выходе звена к прямому
преобразованию Лапласа входного сигнала
при нулевых начальных условиях.
то
отношение прямого преобразования
Лапласа сигнала на выходе звена к прямому
преобразованию Лапласа входного сигнала
при нулевых начальных условиях.
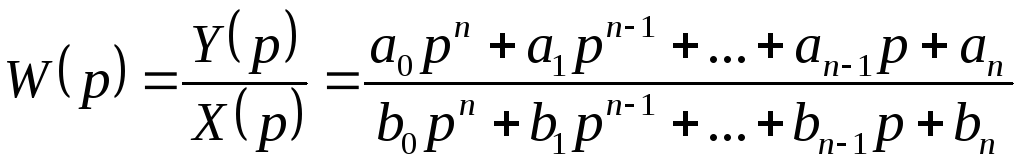
Афх. Если параметруp придать значение j, где и в передаточной функции заменить всеp , то получим:
алгебраическая:
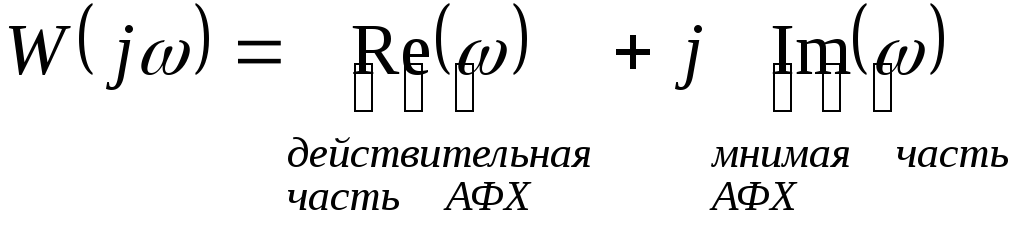
п
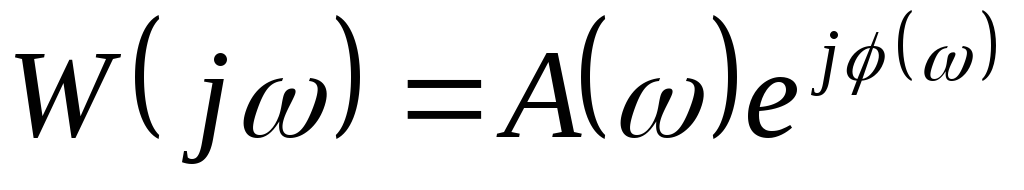
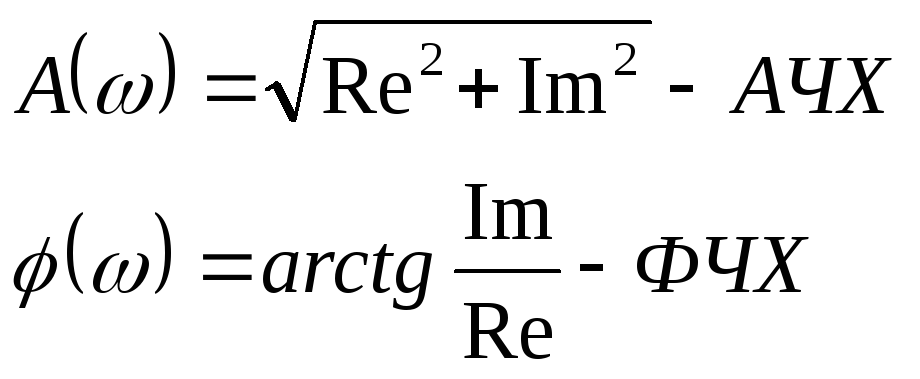 оказательная:
оказательная:
A()модуль АФХ
()аргумент АФХ.
Переход:
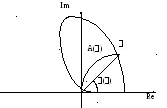
АФХ отношение амплитуды выходного сигнала к амплитуде входного сигнала. () угол сдвига выходного сигнала по отношению к входному.
АФХ
строится в комплексной плоскости:![]()
Изменяем
от
![]() до +
до +![]() ,
фиксируемRe,
Im.
По ним выстраивается график.
,
фиксируемRe,
Im.
По ним выстраивается график.
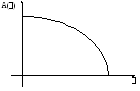
АЧХ
изображается в осях A(), .
Ф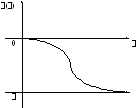 ЧХ:
ЧХ:
Поскольку диапазон изменения частот велик, то прибегают к масштабированию оси частот:

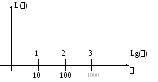
Отрезок, в течении которого частота меняется в 10 раз называется декадой.
9. Временные характеристики.
а) переходная характеристика h(t) переходная функция;
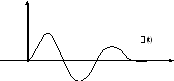
б) импульсная переходная характеристика (t) функция веса.
Переходной характеристикой h(t) называется переходный процесс, возникающий на выходе звена при подаче на вход звена единичного ступенчатого воздействия при нулевых начальных условиях.
Ф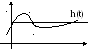
![]()
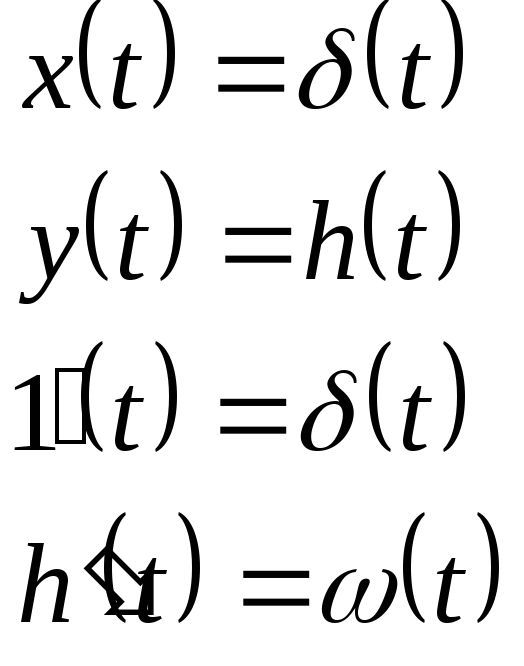 ункция
веса(t)
переходящий
процесс, возникающий на выходе звена
при подаче на вход звена идеального
импульса при нулевых начальных условиях.
ункция
веса(t)
переходящий
процесс, возникающий на выходе звена
при подаче на вход звена идеального
импульса при нулевых начальных условиях.
10. Классификация звеньев. Безынерционное звено.
Это математические модели искусственно выделенных частей системы, характеризующихся простыми алгоритмами.


1![]() 1.Идеальное
интегрирующее звено.
1.Идеальное
интегрирующее звено.
1![]()
![]()
![]() .
Переходная характеристика:
.
Переходная характеристика:
2. Функция веса:
3.Передаточная функция:
4![]()
![]() .АФХ:
.АФХ:
5![]()
![]() .АЧХ:
.АЧХ:
6.ФЧХ:
7. ЛАЧХ:
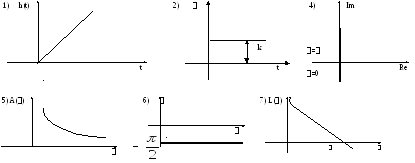
Р![]()
![]() еальное
интегрирующее звено
еальное
интегрирующее звено
П
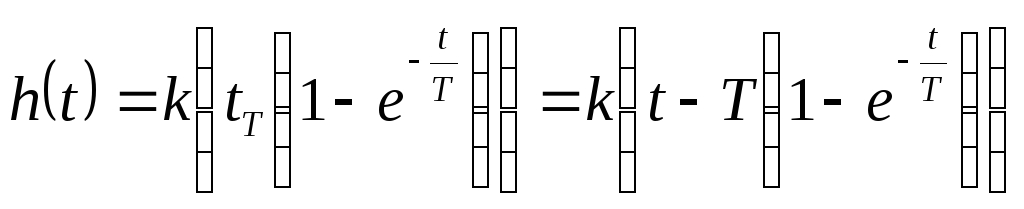 ереходная
функция:
ереходная
функция:Функция Веса:
![]() 3.Передаточная
функция:
3.Передаточная
функция:
![]()
4![]()
![]() .АФХ:
.АФХ:
5.АЧХ:
6![]() .ФЧХ:
.ФЧХ:
7![]() .ЛАЧХ:
.ЛАЧХ:

12. Идеальное дифференцирующее звено.
П
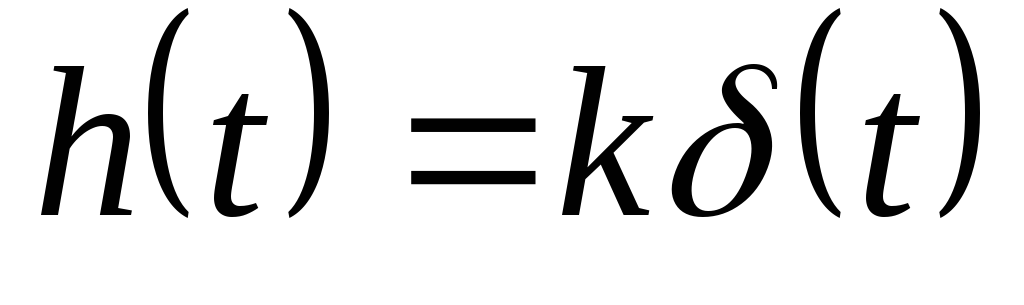
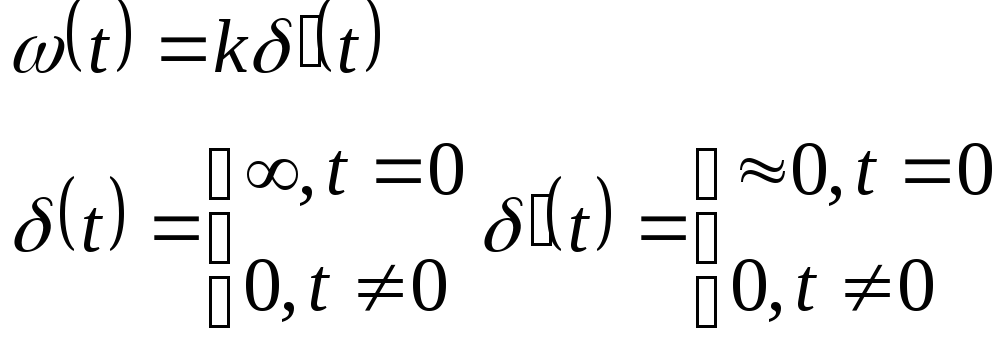 ереходная
характеристика:
ереходная
характеристика:
2.Функция Веса:
3![]() .Передаточная
функция:
.Передаточная
функция:
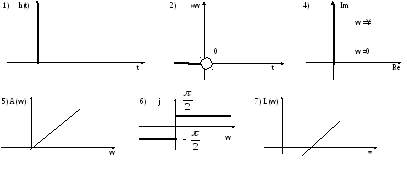
4![]() .АФХ:
.АФХ:
5![]()
![]() .АЧХ:
.АЧХ:
6.ФЧХ:
7.ЛАЧХ:
![]()
![]()
Р![]() еальное
дифференцирующее звено.
еальное
дифференцирующее звено.
1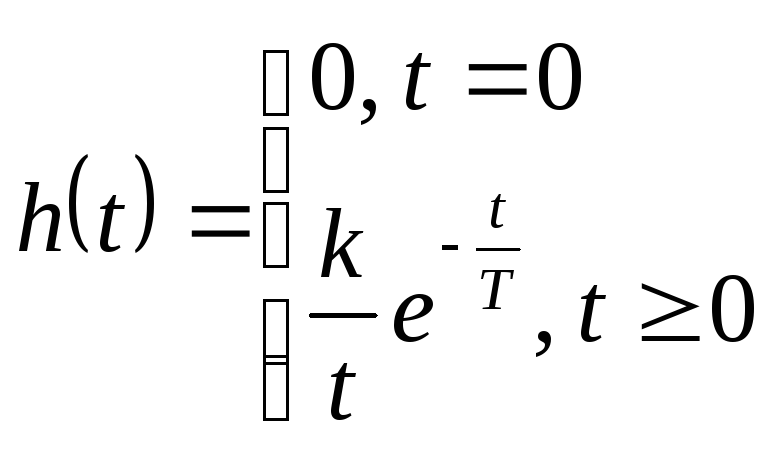 .Переходная
характеристика:
.Переходная
характеристика:
2![]() .Функция
Веса:
.Функция
Веса:
3.Передаточная функция:
![]()
![]()
4![]()
![]() .АФХ:
.АФХ:
5.АЧХ:
6.ФЧХ:
7.ЛАЧХ:
![]()

1![]() 3.
Апериодическое
звено.
3.
Апериодическое
звено.
Динамика процесса описывается следующим уравнением:
k коэффициент усиления
Т постоянная
времени
постоянная
времени
1.Переходная характеристика:
2. Импульсная переходная характеристика (функция веса):
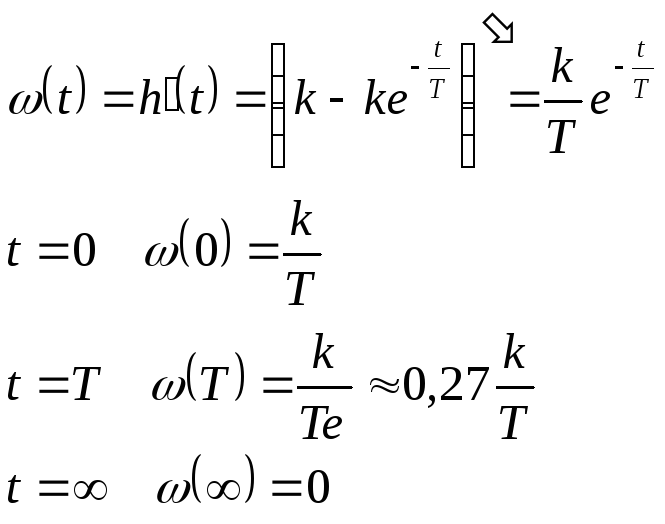
3.Передаточная функция:
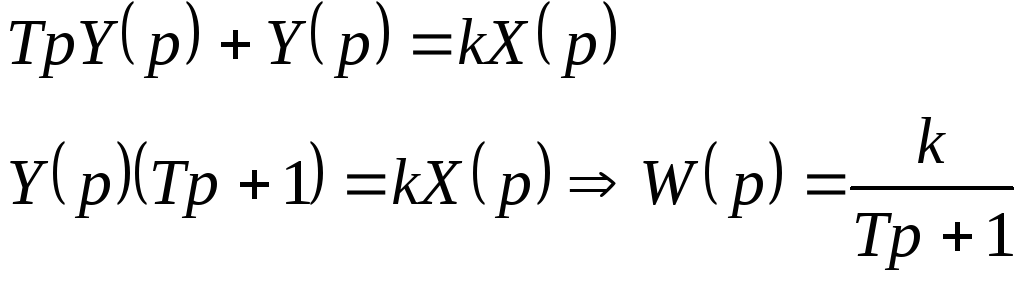
5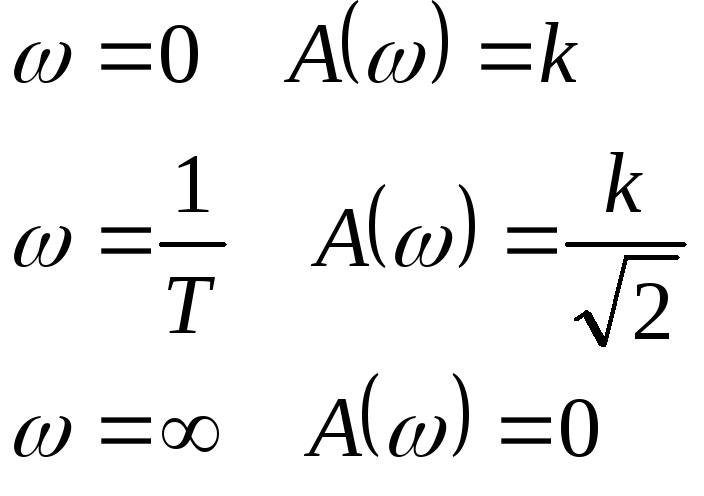 .АЧХ:
.АЧХ:
6![]() .ФЧХ:
.ФЧХ:
![]()
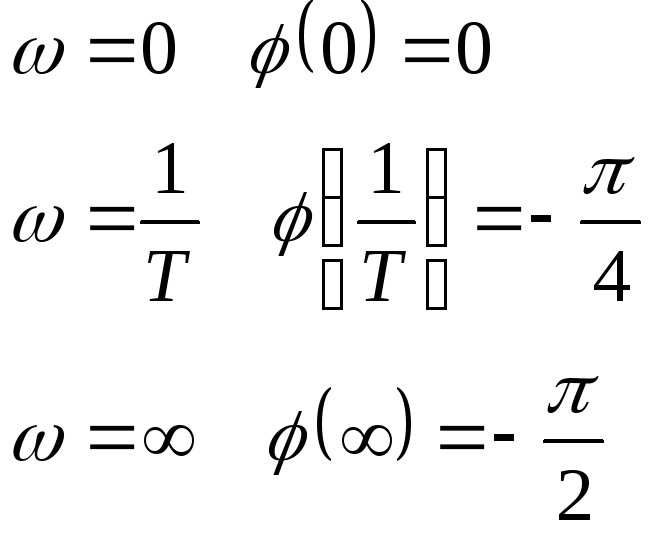
7.ЛАЧХ:
![]()
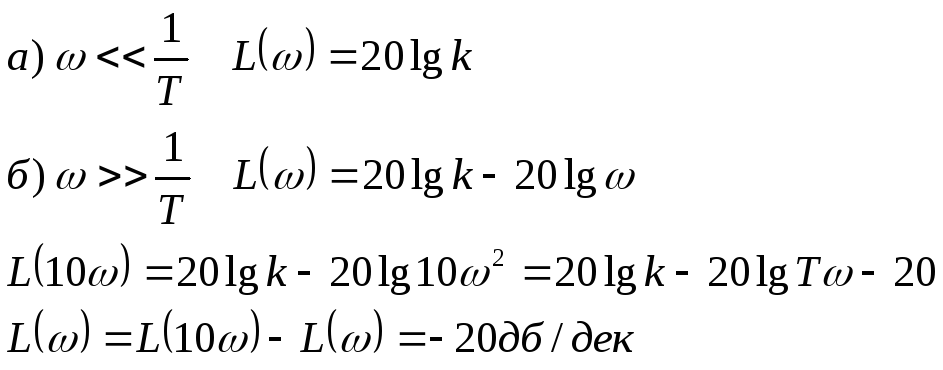
асимптотическая
![]()
 сопрягающая
частота.
сопрягающая
частота.
14. Форсирующее звено.
С![]()
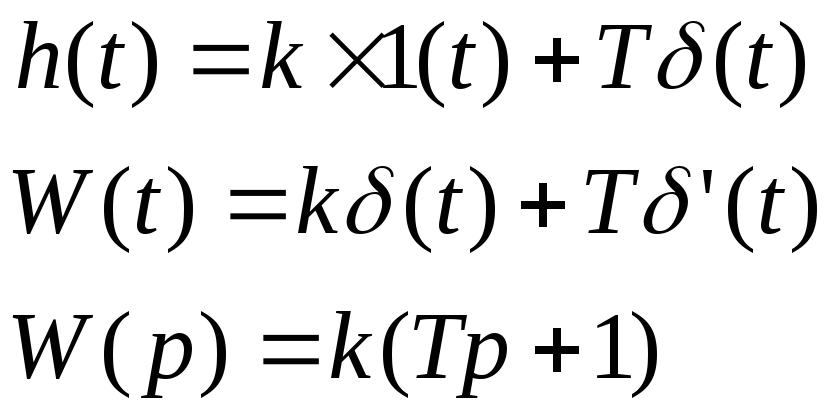 войства
как у диф звеньев. При подаче на вход
сигнала, на выходи достигается величина,
а потом 0. В статике сигналы не пропускаются.
Фильтр высокой частоты. Положительное
влияние на устойчивость системы, так
как положительный фазовый сдвиг.
войства
как у диф звеньев. При подаче на вход
сигнала, на выходи достигается величина,
а потом 0. В статике сигналы не пропускаются.
Фильтр высокой частоты. Положительное
влияние на устойчивость системы, так
как положительный фазовый сдвиг.
1![]() 5.
Колебательное звено.
5.
Колебательное звено.
k коэффициент усиления
Т постоянная времени
![]() коэффициент
демпфирования (гашения).
коэффициент
демпфирования (гашения).
В
зависимости от
![]() различают четыре типа звеньев:
различают четыре типа звеньев:
а)
колебательное 0<![]() <1
<1
б)
апериодическое звено II
порядка![]() >1
>1
в)
консервативное звено
![]() =0
=0
г)
неустойчивое колебательное звено
![]() <0
<0
Переходная характеристика:
а)
![]()
ч![]() ем
больше
ем
больше![]() ,
тем меньше амплитуда колебаний
,
тем меньше амплитуда колебаний
чем меньше Т, тем быстрее устанавливаются переходные процессы.


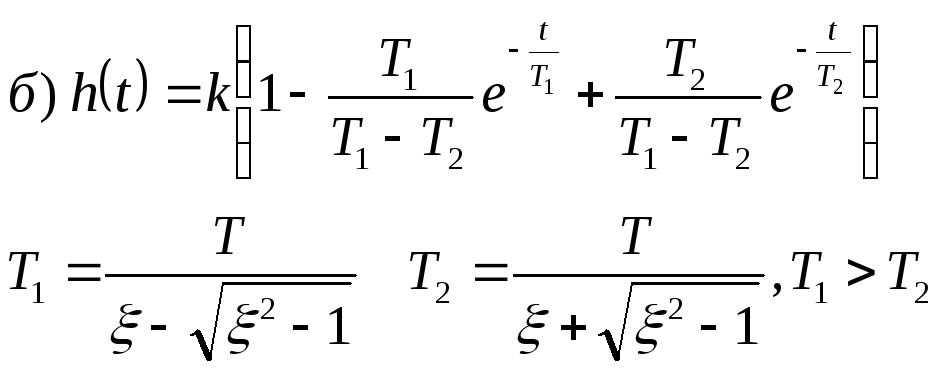

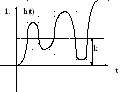
![]()
![]()
г
c t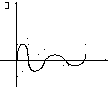
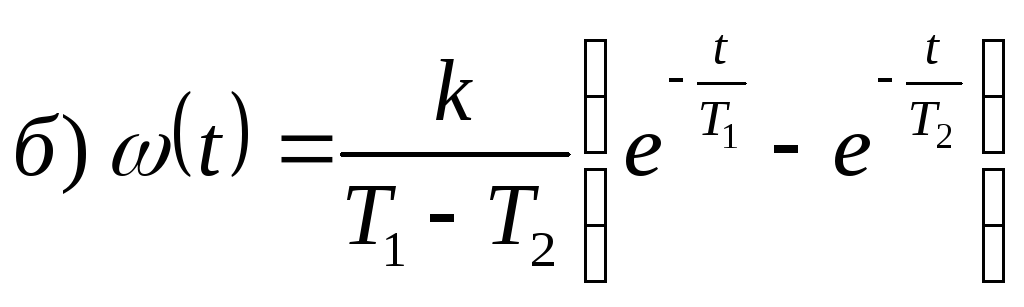 )
аналогично а)
)
аналогично а)
2 .Функция
Веса:
.Функция
Веса:![]()
![]()

3.Передаточная функция:
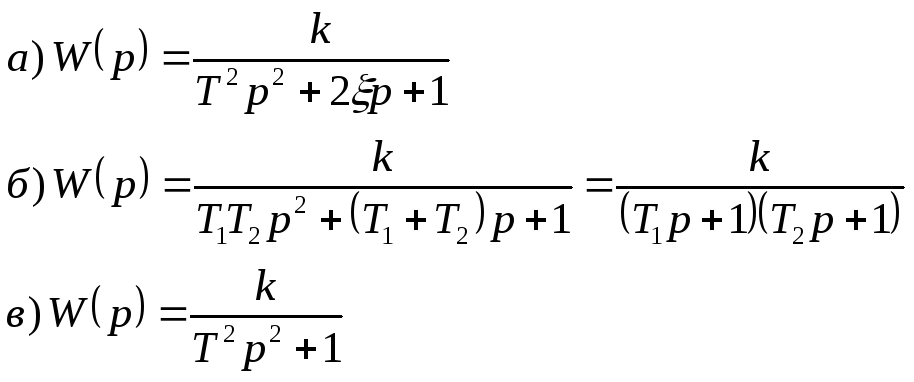
![]()
4.АФХ:
Х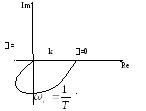
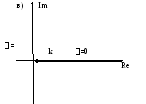 арактеристика
для колебательного звена и для
апериодического звена второго порядка.
арактеристика
для колебательного звена и для
апериодического звена второго порядка.
Для
апериодического
![]() .
.
5.АЧХ:
![]()

6![]() .ФЧХ:
.ФЧХ:

7.ЛАЧХ:
![]()