
- •Утверждение 5 (о запаздывании аргумента). Для любого действительного числа имеет место соотношение: .
- •Свертка функций. Отыскание оригинала по изображению. Сверткой функций будем называть функцию .
- •Изображение периодического оригинала.
- •Задачи на расчет электрических контуров.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Операционное исчисление
Один
из многочисленных способов решения
обыкновенных линейных дифференциальных
уравнений с постоянными коэффициентами
основан на рассмотрении операции
дифференцирования неизвестной функции
как некоторого оператора:
![]() .
.
Описывая
свойства и операции, возможные для
оператора
![]() ,
получим возможность построения решения
дифференциальных уравнений, их систем
и интегро-дифференциальных уравнений
методами линейной алгебры. Предложенный
метод называют символическим или
операторным.
,
получим возможность построения решения
дифференциальных уравнений, их систем
и интегро-дифференциальных уравнений
методами линейной алгебры. Предложенный
метод называют символическим или
операторным.
В
условиях операционного исчисления
оператору
![]() придают смысл произвольной комплекснозначной
переменной
придают смысл произвольной комплекснозначной
переменной![]() ,
связанной с неизвестной функцией
,
связанной с неизвестной функцией![]() преобразованием Лапласа. В этом случае
переход от дифференциального уравнения
к алгебраическому уравнению осуществляется
операциями умножения и интегрирования,
отсюда и название метода. Определяющим
в этом переходе является интегрирование,
что породило и другое название
предлагаемого метода – интегральное
преобразование.
преобразованием Лапласа. В этом случае
переход от дифференциального уравнения
к алгебраическому уравнению осуществляется
операциями умножения и интегрирования,
отсюда и название метода. Определяющим
в этом переходе является интегрирование,
что породило и другое название
предлагаемого метода – интегральное
преобразование.
Оригинал. Изображения. Преобразование Лапласа.
Нахождение изображений.
Комплекснозначная
функция
![]() действительного переменного называетсяоригиналом,
если она удовлетворяет следующим трём
условиям:
действительного переменного называетсяоригиналом,
если она удовлетворяет следующим трём
условиям:
1.
![]() для всех
для всех![]() ;
;
2.
![]() – абсолютно интегрируема на любом
отрезке
– абсолютно интегрируема на любом
отрезке![]() положительной полуоси;
положительной полуоси;
3.
существуют действительные числа
![]() ,
,![]() и
и![]() ,
такие, что
,
такие, что![]() при всех
при всех![]() .
.
Выбор описанных выше условий обусловлен рядом причин:
1. В класс рассматриваемых функций должны попасть все функции, получаемые в качестве частных решений линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, в правой части которых стоят функции того же класса, при произвольных начальных условиях, заданных для некоторого начального значения аргумента. Последнее всегда можно считать нулевым. Это и позволяет наложить условие 1, так как поведение решения нужно знать лишь для значений аргумента, больших начального. Отметим, что для решений линейных дифференциальных уравнений рассматриваемого вида оно оказывается выполненным автоматически.
2.
Ко всем функциям рассматриваемого
класса нужно иметь возможность применять
преобразование Фурье. Последнее, при
выполнении условия 2, снова потребует
наложения условия 1 (чтобы функция
![]() ,
где
,
где![]() ,
при всяком
,
при всяком![]() была абсолютно интегрируема вдоль всей
оси
была абсолютно интегрируема вдоль всей
оси![]() ,
включая ее отрицательную часть) и условия
3.
,
включая ее отрицательную часть) и условия
3.
К
функции
![]() ,
нельзя применить формулу Фурье, так как
она не является абсолютно интегрируемой
вдоль всей оси
,
нельзя применить формулу Фурье, так как
она не является абсолютно интегрируемой
вдоль всей оси![]() .
Но при этом, вспомогательная функция
.
Но при этом, вспомогательная функция![]() уже будет обладать этим свойством.
уже будет обладать этим свойством.
Простейшим
оригиналом является функция
Хевисайда,
определяемая следующим образом:
![]()
![]()
Заметим,
что если функция
![]() удовлетворяет
условиям 2 и 3, то функция
удовлетворяет
условиям 2 и 3, то функция
![]() удовлетворяет условиям 1-3, то есть
является оригиналом. Для упрощения
записи в дальнейшем, за редким исключением,
сомножитель
удовлетворяет условиям 1-3, то есть
является оригиналом. Для упрощения
записи в дальнейшем, за редким исключением,
сомножитель![]() будем опускать и вместо
будем опускать и вместо![]() будем записывать просто
будем записывать просто![]() .
.
Итак:
пусть
![]() – оригинал, а
– оригинал, а![]() – комплексное число.Изображением
оригинала
– комплексное число.Изображением
оригинала
![]() называется функция
называется функция![]() ,
определяемая равенством:
,
определяемая равенством:
![]() .
.
Функция
![]() называется такжепреобразованием
Лапласа от
функции
называется такжепреобразованием
Лапласа от
функции
![]() .
.
Отметим,
что несобственный интеграл в определении
изображения сходится для значений
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
а определяемая им функция
,
а определяемая им функция![]() является аналитической в полуплоскости
является аналитической в полуплоскости![]() .
.
Обычно
используют следующие обозначения: тот
факт, что
![]() является изображением оригинала
является изображением оригинала![]() ,
записывается так:
,
записывается так:![]() ,
,![]() или
или![]() .
.
Утверждение
1 (единственность
изображения).
Если оригиналы
![]() и
и![]() непрерывны и имеют одно и то же изображение
непрерывны и имеют одно и то же изображение![]() ,
то функции
,
то функции![]() и
и![]() совпадают.
совпадают.
Прежде
чем говорить об остальных свойствах
оригиналов и изображений, условимся
обозначать изображение оригинала той
же буквой, только заглавной (![]() ;
;![]() )
и т.п.
)
и т.п.
Утверждение
2 (свойство
линейности).
Любой линейной комбинации оригиналов
в качестве их изображения соответствует
такая же линейная комбинация их
изображений. Так, например, для произвольных
комплексных постоянных
![]() и
и![]() справедливо соотношение:
справедливо соотношение:![]() .
.
Утверждение
3 (о
подобии).
Для любого действительного
![]() справедливо соотношение:
справедливо соотношение:![]() .
.
Утверждение
4 (о
смещении аргумента).
Для любого комплексного числа
![]() имеет место следующая связь между
оригиналом и изображением:
имеет место следующая связь между
оригиналом и изображением:![]() .
.
Утверждение 5 (о запаздывании аргумента). Для любого действительного числа имеет место соотношение: .
Утверждение
6 (о
дифференцировании оригинала).
Если функция
![]() и ее производные являются оригиналами
и
и ее производные являются оригиналами
и![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]()
![]() .
.
Утверждение
7 (о
дифференцировании изображения)
Если
![]() ,то
,то![]() .
В общем случае,
.
В общем случае,![]() .
.
Выпишем
частные случаи этого утверждения:
![]() .
.
Утверждение
8 (об
интегрировании оригинала).
Если
![]() ,
то
,
то
![]() .
.
Утверждение
9 (об
интегрировании изображения).
Если
![]() и интеграл
и интеграл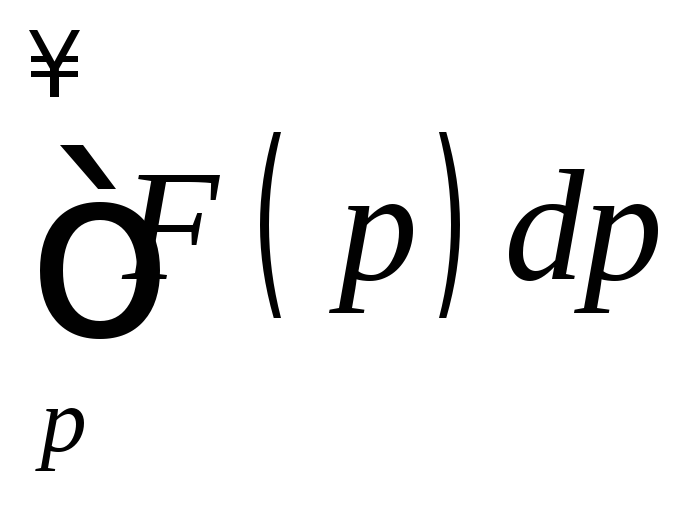 является сходящимся, то
является сходящимся, то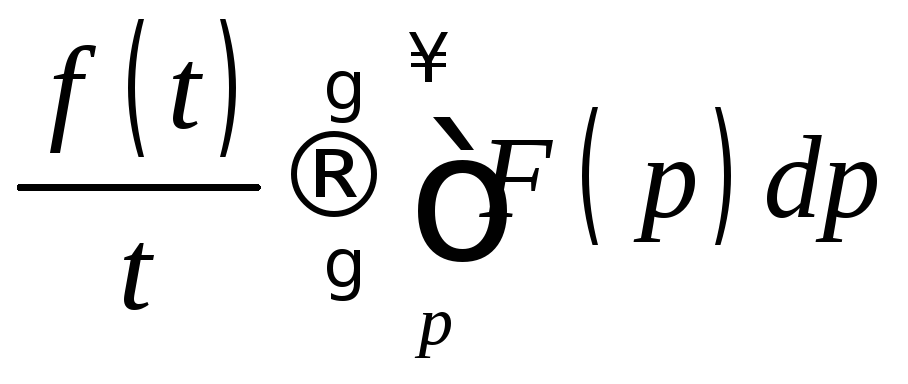 .
.
Утверждения
о дифференцировании и интегрировании
оригиналов демонстрируют тот факт, что
эти операции сводятся соответственно
к умножению и делению на
![]() их изображений.
их изображений.
Приведем
таблицу изображений некоторых основных
функций (как и ранее будем считать, что
![]() и
и![]() – комплексные числа,
– комплексные числа,![]() – натуральное число).
– натуральное число).
Таблица изображений некоторых элементарных оригиналов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем примеры использования определения и результатов утверждений для нахождения изображений.
![]() Найти
изображение функции
Найти
изображение функции
![]() ,
используя преобразование Лапласа.
,
используя преобразование Лапласа.
![]()
![]() Подчеркнем,
что
Подчеркнем,
что
![]() является оригиналом. Так как
является оригиналом. Так как![]() для всех
для всех![]() ,
то изображение
,
то изображение![]() этой функции будет определено и аналитично
в полуплоскости
этой функции будет определено и аналитично
в полуплоскости![]() .
Далее находим:
.
Далее находим:
![]() .
.
![]() Используя
таблицу изображений и свойство линейности
преобразования Лапласа найти
изображения оригинала:
Используя
таблицу изображений и свойство линейности
преобразования Лапласа найти
изображения оригинала:
![]()
![]()
![]() По
таблице изображений найдем:
По
таблице изображений найдем:
![]() .
.
![]() .
.
![]() Найти
изображение функции
Найти
изображение функции
![]() ,
воспользовавшись свойством дифференцирования
изображений.
,
воспользовавшись свойством дифференцирования
изображений.
![]()
![]() Воспользовавшись
таблицей изображений, запишем:
Воспользовавшись
таблицей изображений, запишем:
![]() .
.
Тогда по теореме о дифференцировании получим:
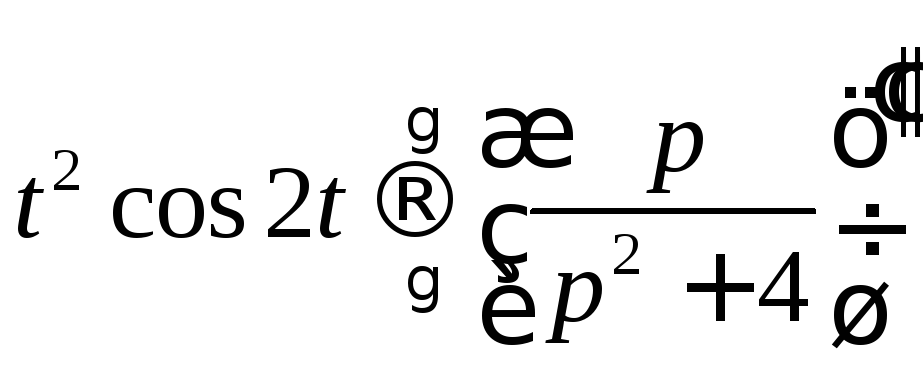 .
.
Последовательно вычисляя производные, находим:
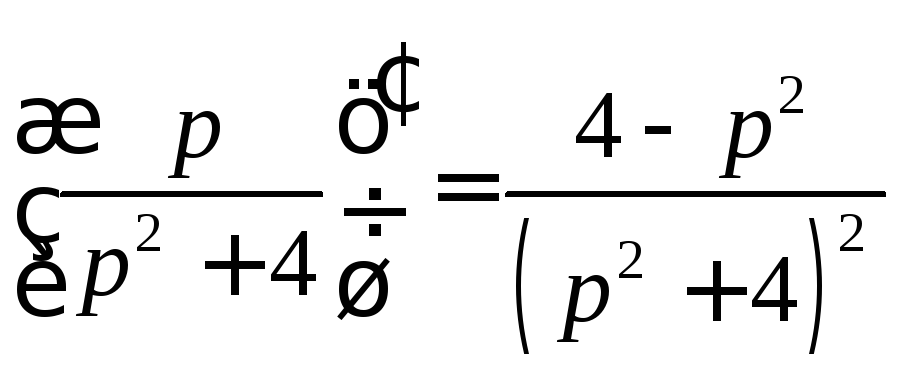 и
далее
и
далее
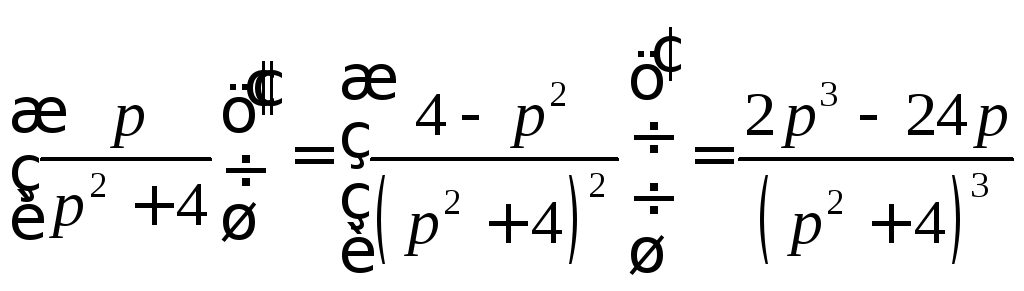 .
.
Окончательно
запишем:
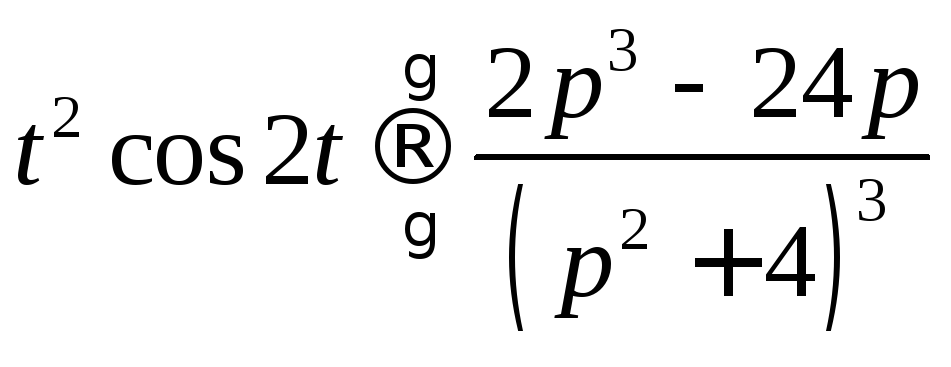 .
.
![]() Найти
изображение функции
Найти
изображение функции
![]() .
.
![]()
![]() Можно,
вычислив интеграл, найти изображение
по таблице изображений. Однако в данном
случае проще воспользоваться теоремой
об интегрировании оригинала. Действительно,
имеем:
Можно,
вычислив интеграл, найти изображение
по таблице изображений. Однако в данном
случае проще воспользоваться теоремой
об интегрировании оригинала. Действительно,
имеем:
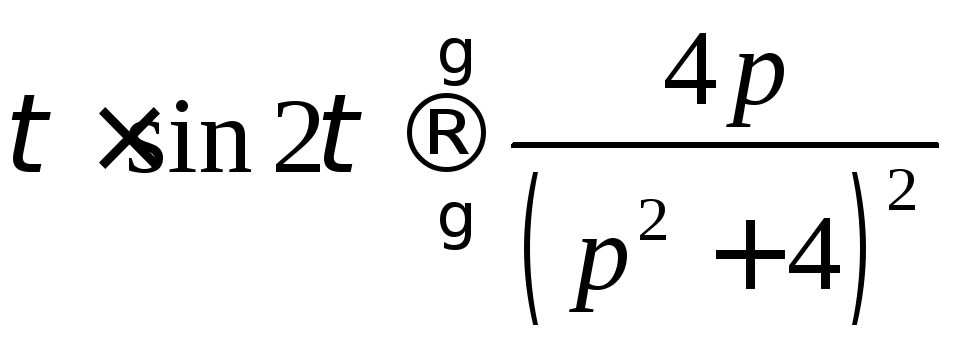 .
Тогда по теореме обинтегрировании
оригинала имеем право, записать:
.
Тогда по теореме обинтегрировании
оригинала имеем право, записать:
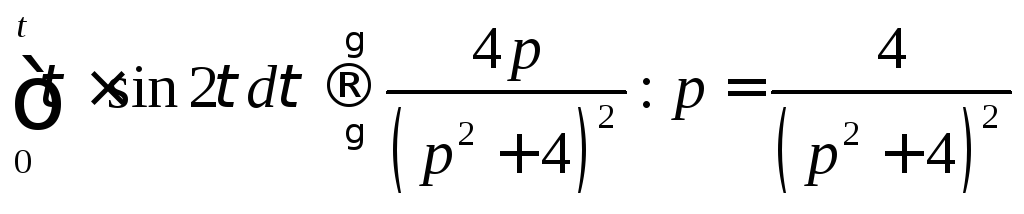 .
.
Свертка функций. Отыскание оригинала по изображению. Сверткой функций будем называть функцию .
Отметим,
что операция свертывания обладает
свойством коммутативности: ![]() ,
то есть
,
то есть
![]() .
.
Утверждение
10 (об
умножении изображений, или теорема о
свертке).
Пусть
![]() ;
;![]() .
Тогда
.
Тогда![]() .
.
Таким образом, изображением свертки двух оригиналов является произведение их изображений.
![]() Найти
свертку функций
Найти
свертку функций
![]() и
и![]() :
:
![]()
![]() Приведем
два способа решения этой задачи.
Приведем
два способа решения этой задачи.
Первый
способ. Воспользуемся таблицей
изображений:
![]() и
и![]() .
.
Воспользовавшись
теоремой о свертке, запишем:
![]() .
.
Итак,
изображение свертки найдено. Найдем
саму свертку. Для этого, как и в предыдущей
задаче, с помощью метода неопределенных
коэффициентов представим дробь в виде
суммы простейших дробей:
![]() .
Тогда по таблице изображений запишем:
.
Тогда по таблице изображений запишем:![]() .
.
Второй
способ.
Вычислим свертку функций, воспользовавшись
определением:
![]() .
.
Интегрируем
по частям:
![]() .
Следовательно,
.
Следовательно,![]() .
.
Теперь
по таблице изображений находим изображение
свертки:
![]() .
.
Итак, нами получен тот же результат.
![]() Пользуясь
теоремой о свертке, найти оригинал
изображения:
Пользуясь
теоремой о свертке, найти оригинал
изображения:
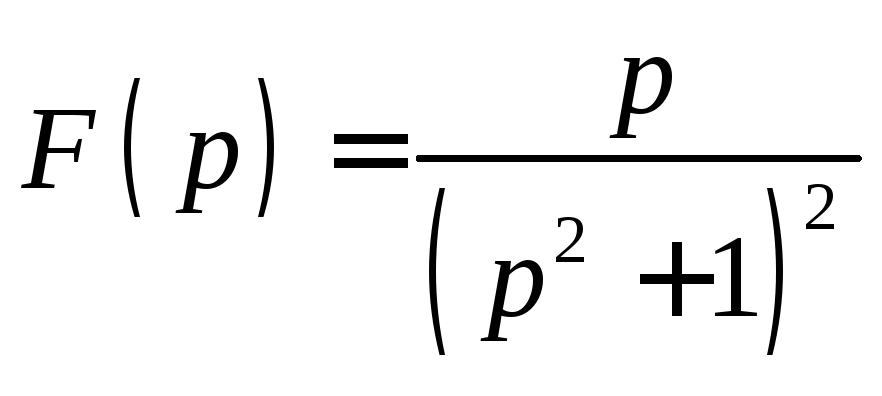 .
.
![]()
![]() Представим
изображение
Представим
изображение
![]() в виде произведения
в виде произведения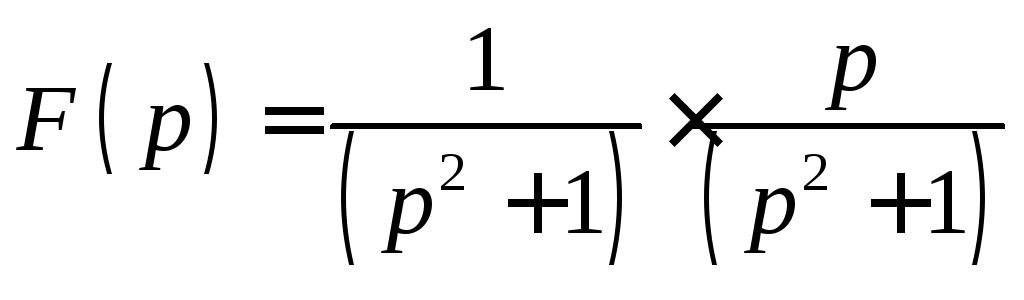 .
По теореме о свертке имеем:
.
По теореме о свертке имеем: .
Найдем теперь свертку функций
.
Найдем теперь свертку функций![]() и
и![]() :
:
![]()
![]() .
.
Таким
образом,
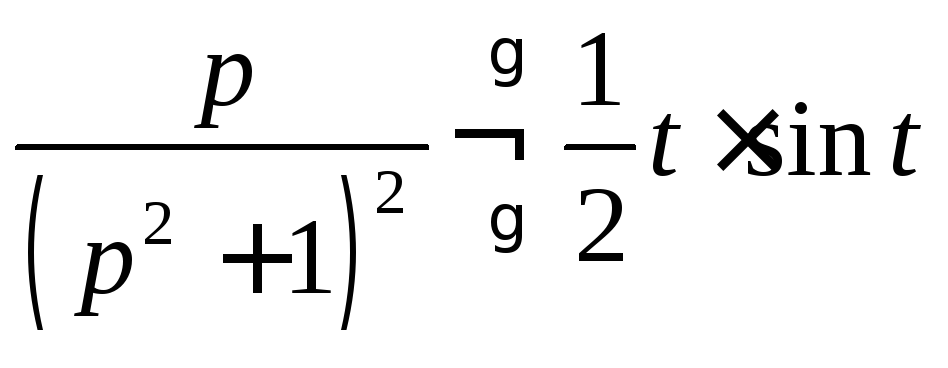 .
.
Заметим, что в данном случае оригинал можно было найти и по таблице изображений.
При нахождении оригиналов по заданным изображениям можно использовать несколько приемов.
Первый
состоит в
том, что изображение
![]() представляется в виде суммы элементарных
дробей, каждая из которых является
изображением простых оригиналов. Далее,
используя таблицу оригиналов и свойство
линейности преобразования Лапласа,
находят оригинал, соответствующий
исходной дроби.
представляется в виде суммы элементарных
дробей, каждая из которых является
изображением простых оригиналов. Далее,
используя таблицу оригиналов и свойство
линейности преобразования Лапласа,
находят оригинал, соответствующий
исходной дроби.
Второй способ состоит в том, чтобы представить дробь в виде произведения дробей, каждая из которых является изображением некоторой функции, и применить теорему о свертке.
Третий способ основан на следующем утверждении:
Утверждение
11 (о
разложении).
Пусть функция
 представляет собой правильную рациональную
дробь, имеющую полюсы в точках
представляет собой правильную рациональную
дробь, имеющую полюсы в точках![]() ,
где
,
где![]() .
Тогда оригиналом для неё служит функция
.
Тогда оригиналом для неё служит функция![]() ,
где сумма берется по всем полюсам.
,
где сумма берется по всем полюсам.
Отметим, что данное утверждение допускает некоторое упрощение в случае, когда
а)
все корни многочлена, стоящего в
знаменателе изображения имеют кратность
единица:
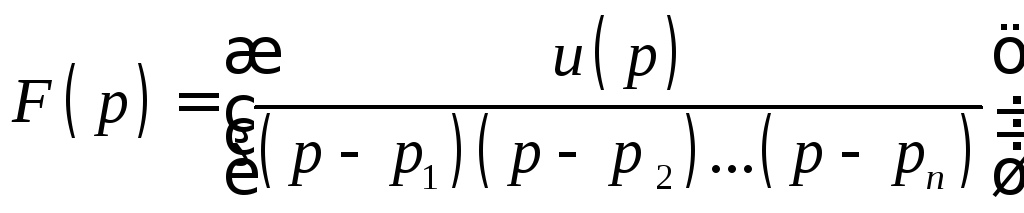
![]()
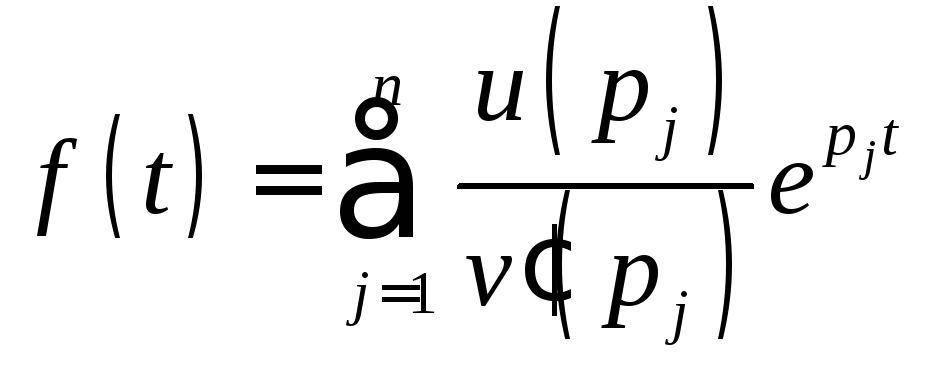 ,
,
б) корни многочлена, стоящего в знаменателе изображения кратные:
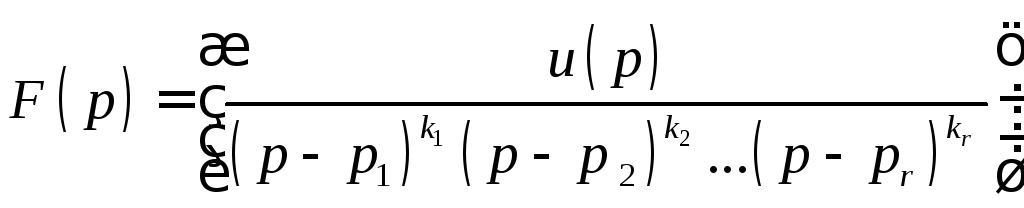
![]()
 ,
,
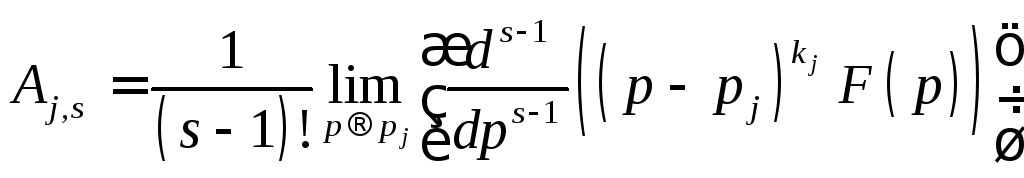 .
.
Приведем примеры использования вышеперечисленных идей при решении задач.
![]() Найти
оригинал изображения:
Найти
оригинал изображения:
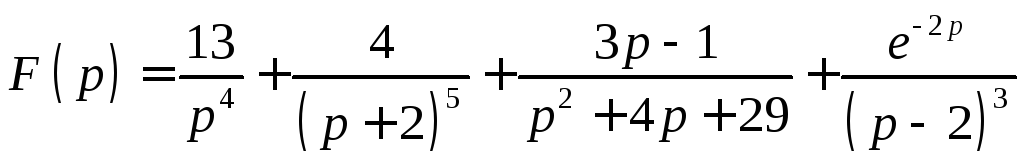 .
.
![]()
![]() При
работе с первым слагаемым по таблице
изображений находим:
При
работе с первым слагаемым по таблице
изображений находим:
![]() .
Поэтому, по свойству линейности
преобразования Лапласа, находим
соответствующий оригинал:
.
Поэтому, по свойству линейности
преобразования Лапласа, находим
соответствующий оригинал:![]() .
.
Аналогично
преобразуем второе слагаемое в выражении:
![]() .
.
Для
нахождения оригинала, соответствующего
третьему слагаемому
![]() выделим полный квадрат в знаменателе:
выделим полный квадрат в знаменателе:![]() .
С учетом этого запишем:
.
С учетом этого запишем: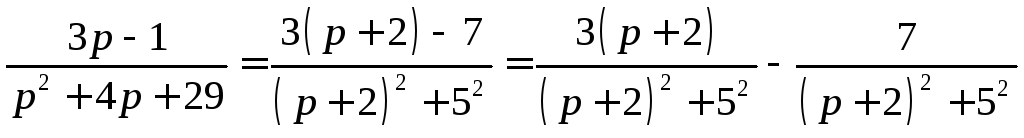 .
Окончательно для этого слагаемого
получим:
.
Окончательно для этого слагаемого
получим: .
.
Для
нахождения оригинала, соответствующего
последнему слагаемому
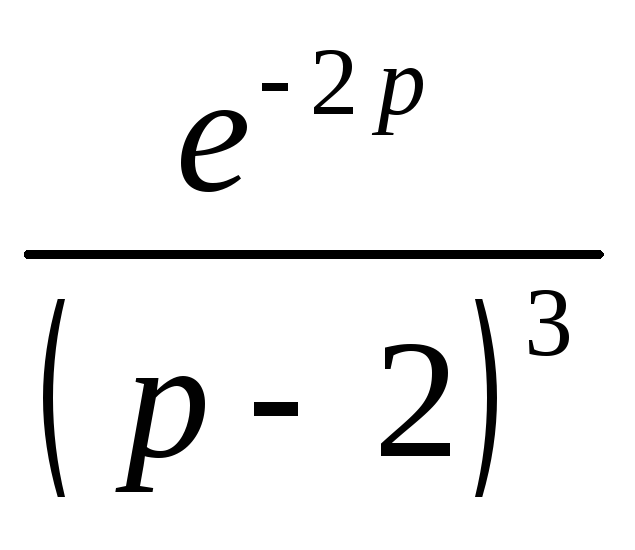 ,
воспользуемся утверждением запаздывания
оригинала. Так как оригинал
,
воспользуемся утверждением запаздывания
оригинала. Так как оригинал![]() для функции
для функции![]() :
:![]() ,
то, применив теперь теорему запаздывания
оригинала, имеем
,
то, применив теперь теорему запаздывания
оригинала, имеем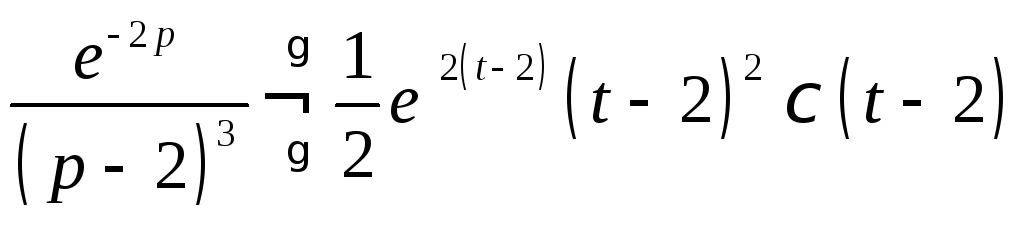
Итак, оригинал, соответствующий нашему изображению имеет вид:
![]() .
.
![]() Найти
оригинал изображения:
Найти
оригинал изображения:
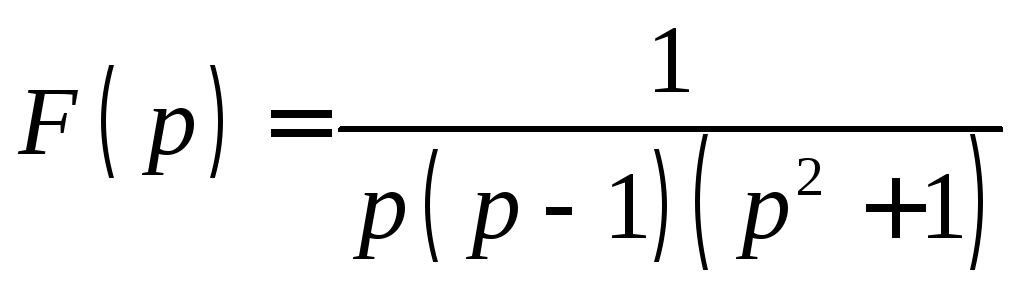 .
.
![]()
![]() Представим
дробь в виде суммы простейших дробей
Представим
дробь в виде суммы простейших дробей
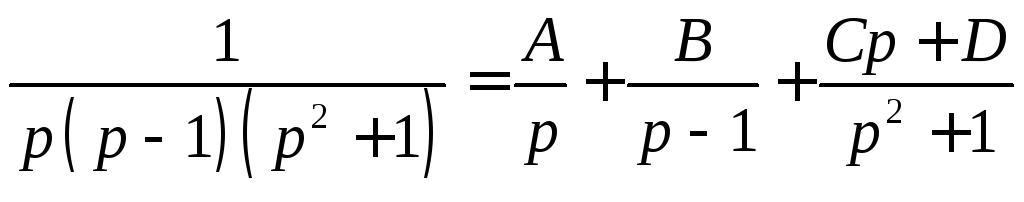 .
.
Воспользуемся
стандартной техникой нахождения
неопределенных коэффициентов
![]() .
Приведем правую часть равенства к общему
знаменателю. Тогда дроби равны, знаменатели
равны, а значит, и числители равны:
.
Приведем правую часть равенства к общему
знаменателю. Тогда дроби равны, знаменатели
равны, а значит, и числители равны:![]() .
.
Слева и справа у нас многочлены. По теореме о равенстве двух многочленов два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях неизвестного. Тогда запишем соответствующую систему и вычислим коэффициенты разложения:
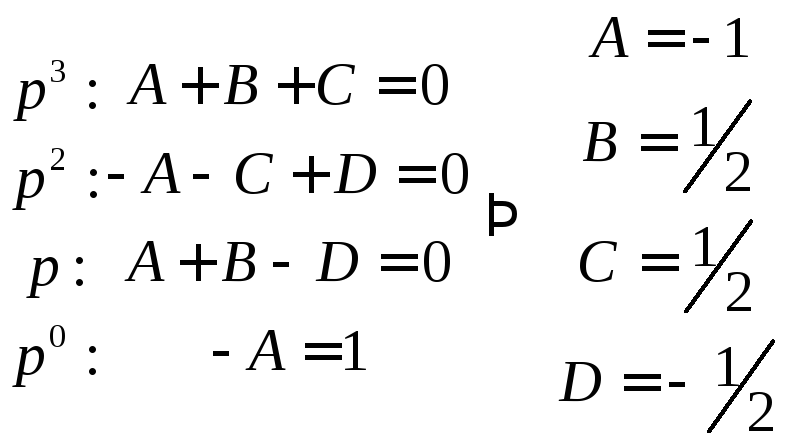 .
.
Таким
образом, исходную дробь представим в
виде
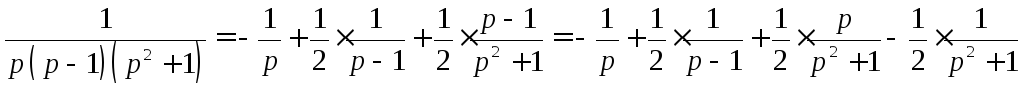 .
.
Следовательно,
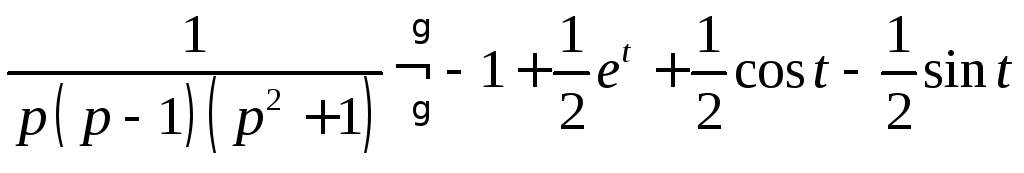 .
.
Проиллюстрируем теперь использование теоремы о разложении для нахождения оригиналов, соответствующих изображениям.
![]() Пользуясь теоремой о разложении, найти
оригинал изображения:
Пользуясь теоремой о разложении, найти
оригинал изображения: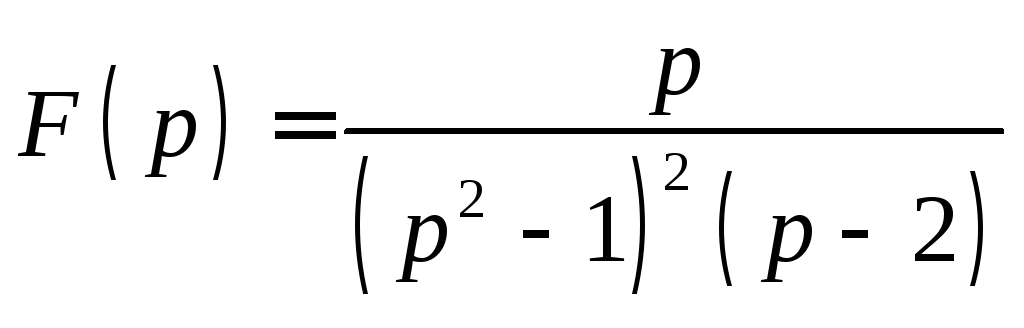 .
.
![]()
![]() Функция
Функция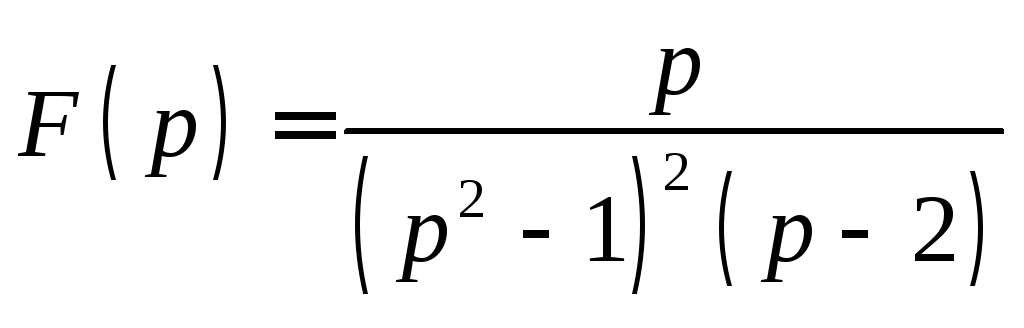 имеет полюсы второго порядка:
имеет полюсы второго порядка:![]() ,
,![]() и полюс первого порядка
и полюс первого порядка![]() .
Тогда по тереме о разложении оригиналом
для
.
Тогда по тереме о разложении оригиналом
для![]() служит функция
служит функция![]() .
Вычислим соответствующие вычеты
.
Вычислим соответствующие вычеты![]() .
.
 ,
,
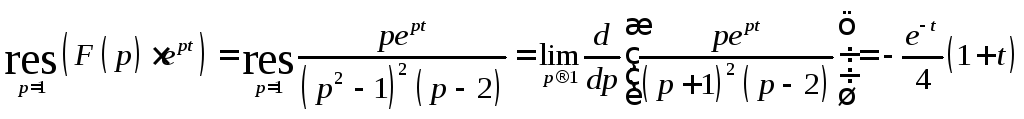 ,
,
 .
.
Следовательно, имеем право, записать
![]() .
.
![]() Найти оригинал изображения:
Найти оригинал изображения:![]() .
.
![]()
![]() Заметим,
что все корни знаменателя действительные
и простые.
Заметим,
что все корни знаменателя действительные
и простые.
При
этом
![]() ,
а
,
а![]() и
и![]() .
.
Итак,
корни многочлена знаменателя:
![]() .
.
Найдем
соответствующие коэффициенты:
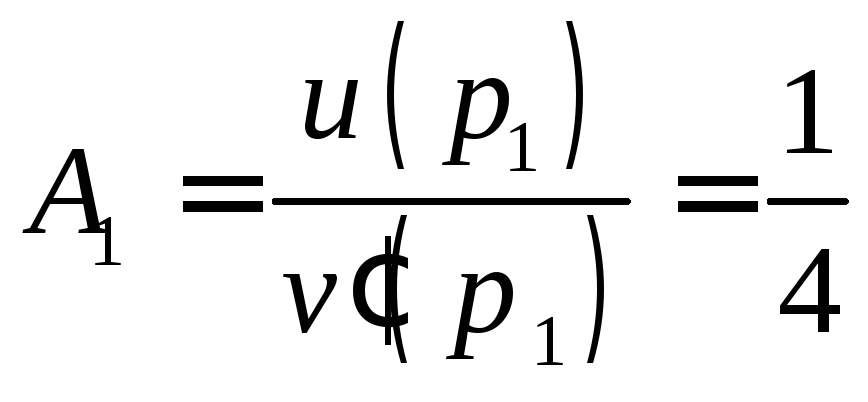 ,
,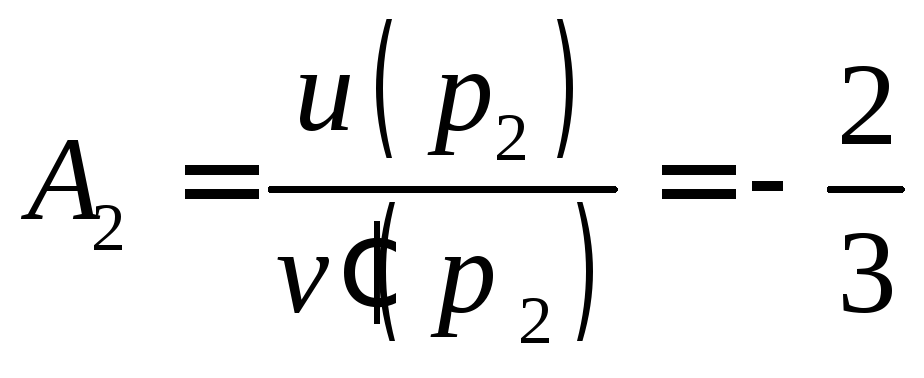 ,
,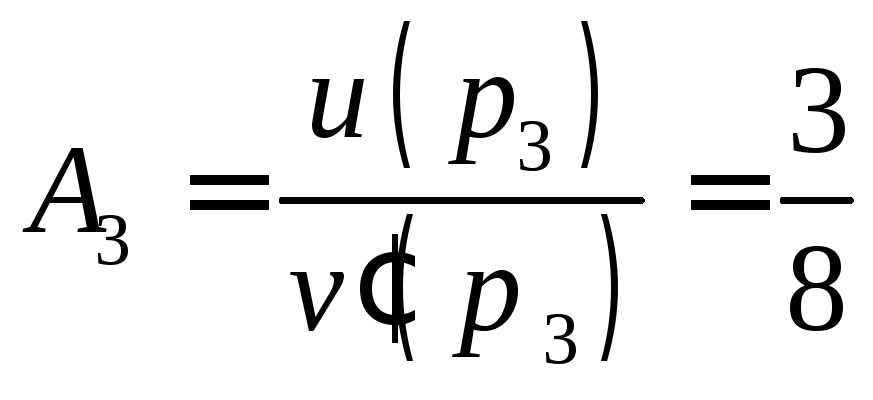 ,
,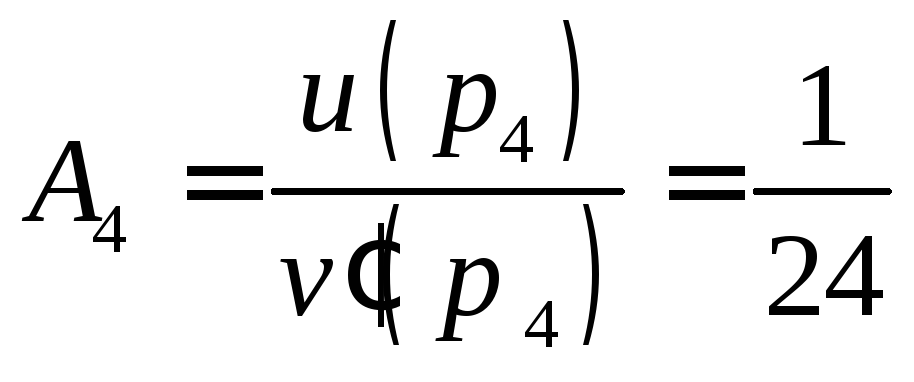 .
.
Следовательно,
![]() .
.
Приведем также пример ситуации с кратными корнями.
![]() Найти оригинал изображения:
Найти оригинал изображения:![]() .
.
![]()
![]() Разложение
изображения на простые дроби имеет вид:
Разложение
изображения на простые дроби имеет вид: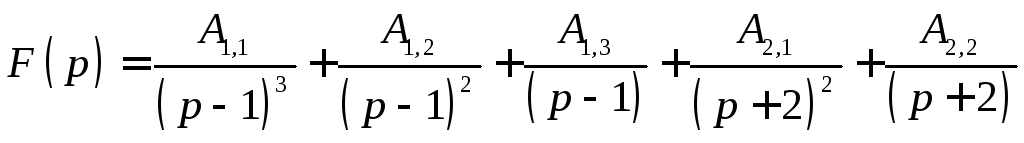 .
.
Найдем коэффициенты этого разложения
![]() ;
;
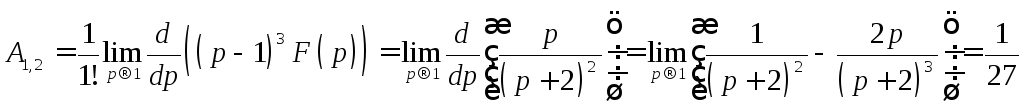 ;
;
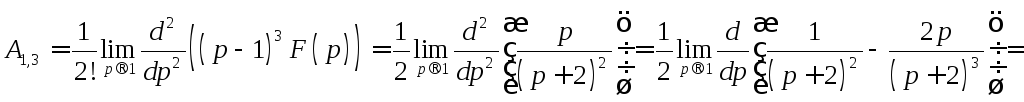
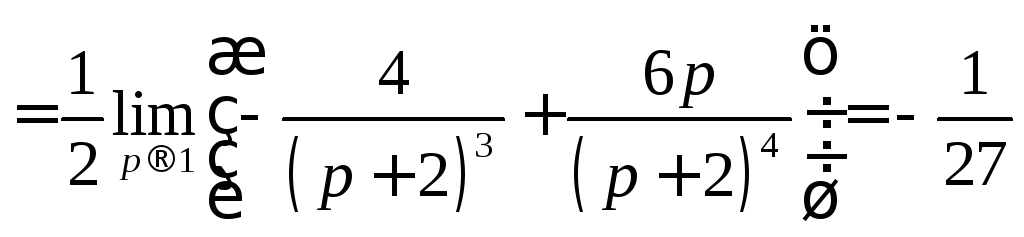 ;
;
![]() ;
;

??????????
Методы операционного исчисления удобно использовать при решении некоторых дифференциальных и интегро-дифференциальных уравнений, а также систем таких уравнений. При этом предполагают, что в правой части такого уравнения стоит оригинал некоторой функции. Приведем примеры использования утверждений, касающихся свойств оригиналов и изображений.
![]() Найти
частное решение дифференциального
уравнения
Найти
частное решение дифференциального
уравнения
![]() .
.
![]()
![]() Пусть
функция
Пусть
функция
![]() ,
удовлетворяющая данному уравнению
имеет изображение:
,
удовлетворяющая данному уравнению
имеет изображение:
![]() .
Тогда воспользовавшись утверждением
о дифференцируемости оригинала запишем:
.
Тогда воспользовавшись утверждением
о дифференцируемости оригинала запишем:
![]() ,
а
,
а
![]() .
.
Правая часть уравнения преобразуется следующим образом:
![]() .
.
Приходим
к операторному уравнению:
![]() .
.
Выразим
из полученного уравнения изображение
![]() частного
решения дифференциального уравнения:
частного
решения дифференциального уравнения:
 .
.
Найдем разложение получившейся дроби на сумму дробей, представляющих собой оригиналы элементарных функций.
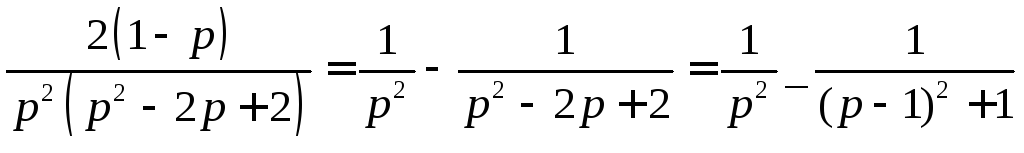 .
.
Следовательно,
![]() решение исходной задачи Коши.
решение исходной задачи Коши.
![]() Найти
общее решение дифференциального
уравнения
Найти
общее решение дифференциального
уравнения
![]() .
.
![]()
![]() Выберем
произвольные начальные условия задачи
Коши. Пусть
Выберем
произвольные начальные условия задачи
Коши. Пусть
![]() .
И пусть
.
И пусть
![]() .
Тогда
.
Тогда
![]() и
и
![]() ,
кроме того
,
кроме того
![]() .
И соответствующее операторное уравнение
имеет вид:
.
И соответствующее операторное уравнение
имеет вид:
![]() .
.
Выразим
отсюда
![]() :
:
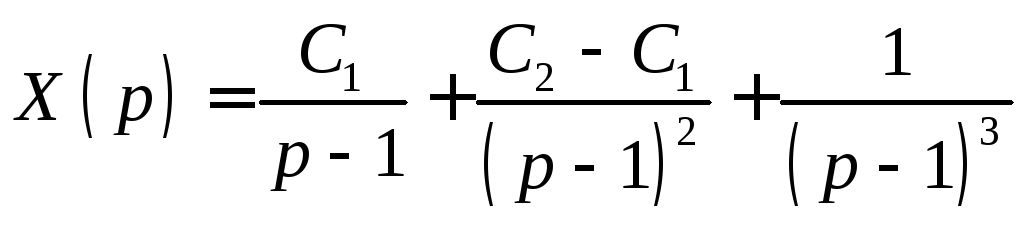 .
.
И значит решением исходного уравнения будет функция
![]() .
(здесь
.
(здесь
![]() ).
).
![]() Решить
интегральное уравнение
Решить
интегральное уравнение
![]() .
.
![]()
![]() Выпишем
уравнение для изображений, воспользовавшись
утверждением 8 об интегрировании
оригинала. (Полагая, что
Выпишем
уравнение для изображений, воспользовавшись
утверждением 8 об интегрировании
оригинала. (Полагая, что
![]() ).
).
![]() .
Выразим функцию изображения
.
Выразим функцию изображения
![]() .
Найдем оригинал, соответствующий данному
изображению
.
Найдем оригинал, соответствующий данному
изображению
![]() .
.
![]() Решить
интегральное уравнение
Решить
интегральное уравнение
![]() .
.
![]()
![]() Отметим,
что левая часть уравнения представляет
собой свертку функций
Отметим,
что левая часть уравнения представляет
собой свертку функций
![]() и
и
![]() .
Переходя к соответствующим изображениям
запишем
.
Переходя к соответствующим изображениям
запишем
![]() .
Выражая из последнего уравнения
.
Выражая из последнего уравнения
![]() убедимся
убедимся
![]() .
И, значит, этому изображению соответствует
оригинал
.
И, значит, этому изображению соответствует
оригинал
![]() .
.
![]() Решить
систему уравнений
Решить
систему уравнений
![]()
![]()
![]() Пусть
Пусть
![]() и
и![]() .Выпишем
соответствующую операторную систему
линейных уравнений
.Выпишем
соответствующую операторную систему
линейных уравнений
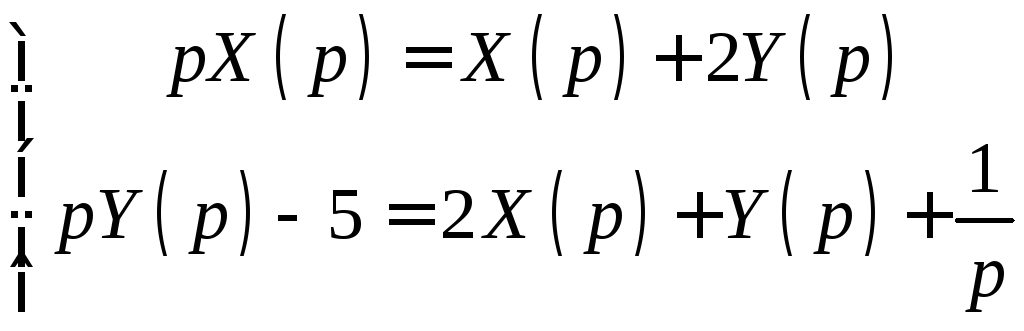 .
.
Выразим
из получившейся операторной системы
![]() и
и
![]() :
:
![]() ,
,
![]() .
.
Отметим, что для нахождения соответствующих оригиналов удобно воспользоваться теоремой разложения, учтя при этом, что корни знаменателя имеют первую кратность.
Таким
образом
![]() ,
и
,
и
![]() .
.
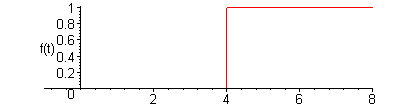
![]() Найти
изображение функции Хевисайда:
Найти
изображение функции Хевисайда:
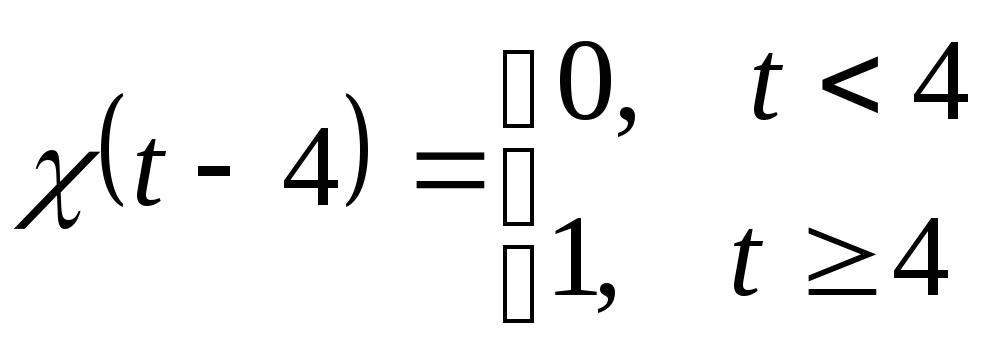 (см. рис.)
(см. рис.)
![]()
![]() Ранее
было получено, что изображением для
оригинала
Ранее
было получено, что изображением для
оригинала
![]() является
функция
является
функция![]() ,тогда,
воспользовавшись теоремой запаздывания,
получим:
,тогда,
воспользовавшись теоремой запаздывания,
получим:
![]()
![]() .
.
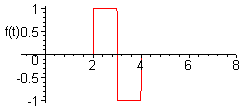
![]() Найти
изображение функции, заданной следующим
графиком:
Найти
изображение функции, заданной следующим
графиком:
![]()
![]() Аналитически
запись этой функции будет выглядеть
следующим образом:
Аналитически
запись этой функции будет выглядеть
следующим образом:
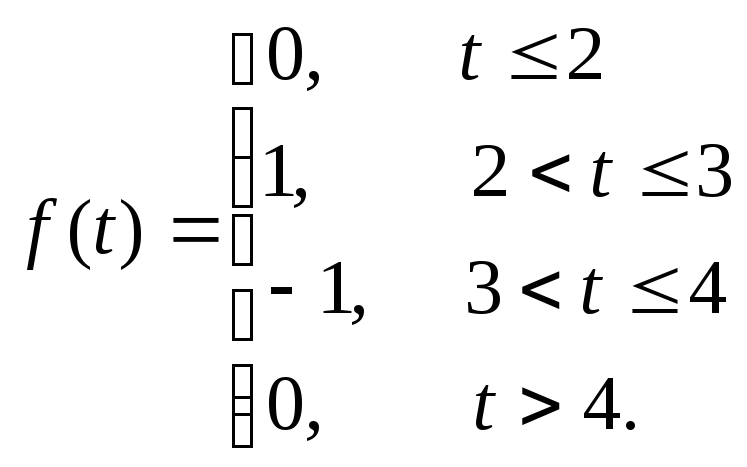
Поэтому ее изображение можно найти, используя формулу преобразования Лапласа, учитывая области определения кусочно-заданного оригинала:
![]()
![]() .
.
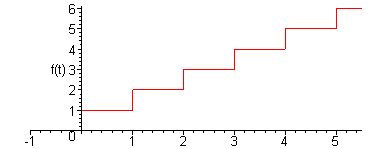
![]() Найти
изображение ступенчатой функции,
изображенной на рисунке.
Найти
изображение ступенчатой функции,
изображенной на рисунке.
![]()
![]() Аналитически
запись этой функции будет выглядеть
следующим образом:
Аналитически
запись этой функции будет выглядеть
следующим образом:
![]() .
Это легко проверяется графическим
сложением функций
.
Это легко проверяется графическим
сложением функций
![]() ,
,![]() ,
,
![]() и т.д., изображенных на одном и том же
чертеже. По теореме запаздывания
получаем:
и т.д., изображенных на одном и том же
чертеже. По теореме запаздывания
получаем:![]()
![]()
![]() .
Второй сомножитель из правой части
равенства представляет собой геометрическую
прогрессию, со знаменателем
.
Второй сомножитель из правой части
равенства представляет собой геометрическую
прогрессию, со знаменателем![]() .
Так как,
.
Так как,![]() ,
то геометрическая прогрессия сходится,
и получаем:
,
то геометрическая прогрессия сходится,
и получаем:![]()
![]()
![]() .
.
