Лабораторная работа № 11 физический маятник

Цель работы: ознакомиться с одним из методов определения ускорения свободного падения.

Оборудование: ЛКМ-2 (физический маятник с отверстиями, пластмассовый фиксатор, измерительная система ИСМ-2).

Краткие теоретические сведения

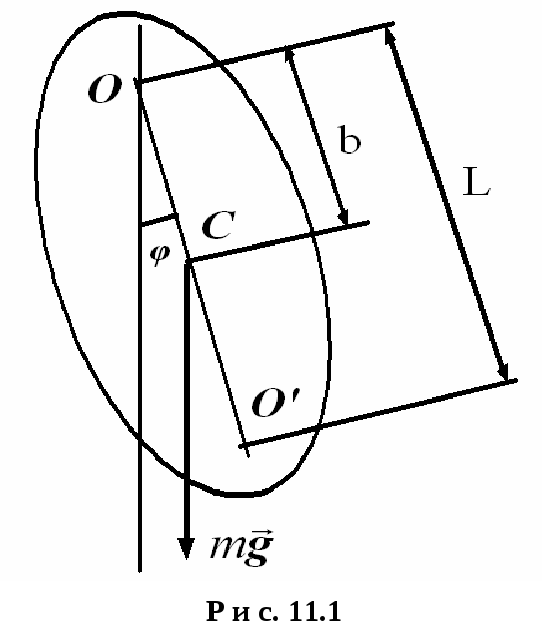
Физическим маятником (ФМ) называется твердое тело, которое может колебаться под действием силы тяжести вокруг горизонтальной оси (не проходящей через центр масс тела).

При колебании ФМ поворачивается вокруг оси О (рис. 11.1). (Кстати, точку О пересечения оси с вертикальной плоскостью, проходящей через центр масс С тела, называют точкой подвеса). Следовательно, движение маятника подчиняется основному уравнению динамики вращательного движения:

или , (11.1)

где М – момент силы тяжести относительно той же оси О.

I – момент инерции маятника относительно той же оси;

–угловое ускорение маятника, из рис. 11.1. видно, что

, (11.2)

где m – масса маятника;

- плечо силы тяжести ;

- расстояние от точки подвеса О до центра масс С.

Знак «» означает, что вращающий момент стремится уменьшить угол, характеризующий положение маятника по отношению к равновесному состоянию. Более строго смысл знака «» объясняется так: псевдовекторы момента сил и смещения от положения равновесиянаправлены в противоположные стороны (для ситуации, изображенной на рис. 11.1, первый направлен за плоскость чертежа, а второй – из этой плоскости на наблюдателя). Помня, что, и, учитывая (11.1), уравнение (11.2) запишем в виде

. (11.3)

При малых отклонениях маятника (именно этот случай мы и будем иметь ввиду) , а потому равенство (11.3) после деления напримет вид

. (11.4)

Величина как сугубо положительная может быть заменена квадратом некоторого числа:

. (11.5)

Тогда уравнение (11.4) можно переписать так

. (11.6)

Используя прямую подстановку, убеждаемся, что решением уравнения (11.6) является выражение

. (11.7)

Это свидетельствует о том, что ФМ совершает в этих условиях незатухающие гармонические колебания с циклической частотой .и постоянные (амплитуда и начальная фаза), зависящие от начальных условий.

Период колебания ФМ

, (11.8)

имеет размерность длины. Эта величина обозначается через и называется приведенной длиной ФМ:

(11.9)

Таким образом,

. (11.10)

Сравнивая (11.10) с формулой для периода колебаний математического маятника , где- длина математического маятника, видим, что приведенная длина ФМ – это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного ФМ. легко заметить, что. В самом деле, в соответствии с теоремой Штейнера, где- момент инерции маятника относительно оси, проходящей через центр масс.

Следовательно, по выражению (11.10)

, (11.11)

откуда видно, что .

Точку (рис. 11.1), отстоящую отна расстояние, называют точкой качаний.

Описание установки и метода определения

И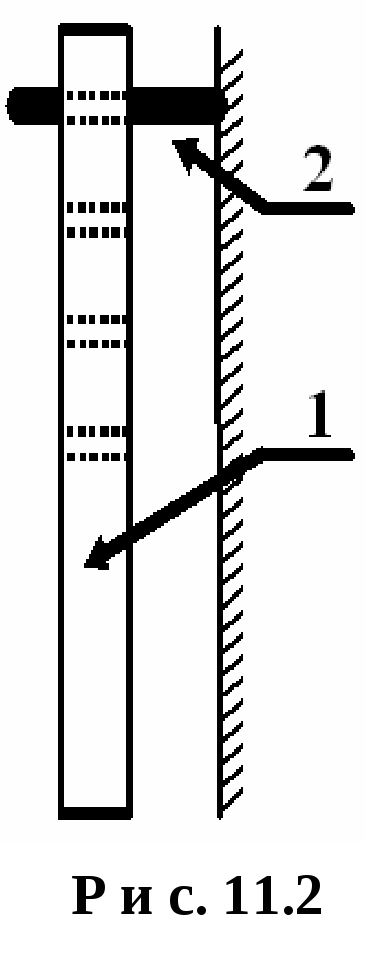сследуемое тело 1 представляет собой металлический стержень с отверстиями (рис. 11.2). Этими отверстиями тело подвешивается на шкив стойки 2, для организации колебаний. На шкив может быть подвешен математический маятник (в данной работе он не используется). Для физического маятника выражение (11.10) с учетом (11.11) представим следующим образом

,

из которого видно, что если b  0, т.е. точка подвеса приближается к центру масс, то T  , и если b  , когда точка подвеса выносится за пределы маятника и удаляется от него (при этом физический маятник превращается в математический), то T снова неограниченно возрастает. Это означает, что расстояние до точки подвеса должно иметь некоторое минимальное значение b_m, при котором период колебаний минимален. Найдем это расстояние. Для стержня , гдеl – длина стержня, выражения для периода колебаний примет вид

.

Минимизируя это выражение по b, получим

.

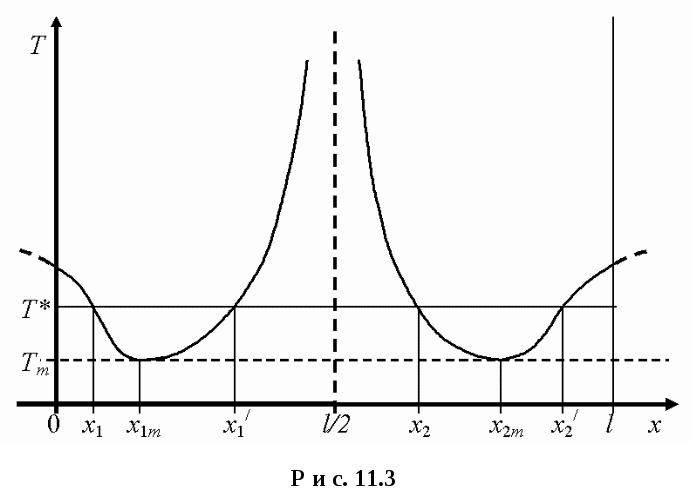
Если вести координату x, измеряемую от конца стержня и учесть, что b_m- это расстояние от середины стержня, то получим два значения координаты x, при которых период колебаний стержня минимален:

и .

График зависимости периода колебаний от координаты точки подвеса приведен на рис. 11.3.