Среднее число заявок в системе
Среднее
число обслуживаемых заявок
.
Среднее
время ожидания в очереди
,
среднее время пребывания заявки в
системе
.
5. Различные системы массового обслуживания
Эта часть учебного пособия содержит разделы, охватывающие большой круг вопросов, содержащих ряд важных приложений теории массового обслуживания к различным областям практической деятельности. Многие реальные процессы могут рассматриваться как представленные в данной главе системы массового обслуживания. За последние годы теории СМО уделялось большое внимание и были получены важные результаты. Вследствие того, что прикладное значение теории СМО возросло, некоторые из новых результатов включены в главу 5.
5.1. Система массового обслуживания с ожиданием и приоритетом в обслуживании
Зачастую при рассмотрении СМО приходится иметь дело с заявками определенного типа, которые должны обслуживаться в первую очередь. Примером такой СМО является аэродром с одной взлетно-посадочной полосой (ВПП). Самолетам, идущим на посадку, ВПП предоставляется в первую очередь, т.е. они пользуются приоритетом в обслуживании по сравнению с самолетами, которые используют ВПП для взлета. Аналогичную картину можно наблюдать на автозаправочной станции (АЗС), где обычно рейсовые автобусы обслуживаются в первую очередь.
В системах массового обслуживания с приоритетом могут быть различные варианты дисциплины обслуживания.
Системами с абсолютным приоритетом называются такие системы, в которых заявка, обладающая приоритетом, немедленно принимается к обслуживанию каналом, занятым обслуживанием заявки без приоритета в обслуживании. Например, если на АЗС прибывает рейсовый автобус, а в это время заправляется легковая машина, то ее заправка прекращается и начинается заправка автобуса. После того, как заявка, обладающая приоритетом, обслужена, а других заявок, обладающих приоритетом, нет, возобновляется прерванное обслуживание заявки, не обладающей приоритетом. Здесь возможны различные варианты: заявка, обслуживание которой было прервано, начинает обслуживаться заново; прерванное обслуживание заявки начинается с того места, где оно было прервано; заявка, обслуживание которой было прервано, вообще теряется.
Системами с относительным приоритетом называются такие системы, в которых заявка, не обладая приоритетом, обслуживается до конца, после чего принимаются к обслуживанию заявки, обладающие приоритетом (если такие имеются).
Из всех возможных СМО с приоритетом здесь рассмотрим только одну, самую простую: одноканальную СМО с абсолютным приоритетом.
Постановка задачи. Рассматривается СМО с абсолютным приоритетом, на вход которой подаются два независимых простейших потока заявок с интенсивностями 1 и 2. Заявки первого потока (интенсивность которого равна 1) обладает приоритетом в обслуживании. Число мест в очереди для заявок обоих видов не ограничено. Если канал обслуживает заявку первого потока, то интенсивность простейшего потока обслуживания равна 1. Если канал обслуживает заявку второго потока, то интенсивность простейшего потока обслуживания равна 2. В этом случае нет различия между двумя вариантами дисциплины обслуживания:
а) прерванное обслуживание заявки начинается с того места, где оно было прервано;
б) заявка, обслуживание которой было прервано, начинает обслуживаться заново.
Это объясняется тем, что интервал времени всего обслуживания и интервал остатка времени обслуживания распределены одинаково по показательному закону с параметрами 2. Граф состояний такой СМО приведен на рис. 5.1.
Рис. 5.1. Граф состояний СМО с бесконечной очередью
и абсолютным приоритетом
Состояние системы будем связывать с числом заявок i, обладающих приоритетом, и числом заявок j, не обладающих приоритетом, находящихся в данный момент t в системе. Рассмотрим различные состояния системы: х0,0 – в системе нет никаких заявок; х0, j – в системе имеется j заявок, не обладающих приоритетом, из этих j заявок одна обслуживается, а j – 1 ждут очереди; хi,0 – в системе имеется i заявок, обладающих приоритетом, и нет заявок, не обладающих приоритетом, из этих i заявок одна обслуживается, а остальные i – 1 ожидают в очереди; хij – в системе имеется i заявок, обладающих приоритетом, и j заявок, не обладающих приоритетом, из i заявок, обладающих приоритетом, одна заявка обслуживается, а i – 1 ожидают в очереди; до тех пор, пока все заявки, обладающие приоритетом, не будут обслужены, заявки, не обладающие приоритетом, не обслуживаются.
Система уравнений имеет следующий вид:
,
,
(5.1)
,
.
Эту систему дифференциальных уравнений обычно интегрируют при следующих начальных условиях: Р0,0(0) = 1; Рi,j(0) = 0 (при i 0 или j 0; в начальный момент система свободна).
Решение системы уравнений для любого момента времени t удовлетворяет условию нормировки:
.
Введем
обозначения:
.
Можно доказать, что стационарный режим работы системы существует только в случае, когда 1 + 2 < 1. Так как величины 1 и 2 положительны, то при этом также должны выполняться условия 1 < 1, 2 < 1.
Найдем стационарный режим работы системы с приоритетами, для чего нужно в уравнениях (5.1) принять все производные равными нулю.
Допустим,
что удалось решить полученную систему
алгебраических уравнений и вероятности
Pi,j
(i
= 0, 1, 2, …; j
= 0, 1, 2, …)
найдены. Тогда вероятность
того,
что в системе будет ровноi
заявок,
обладающих приоритетом (безотносительно
к тому, сколько имеется там заявок, не
обладающих приоритетом), можно найти
по следующей формуле:
.
Вероятность
того,
что в системе имеется ровноj
заявок, не обладающих приоритетом
(безотносительно к тому, сколько имеется
там заявок, обладающих приоритетом),
запишем в виде
.
Так как рассматриваемая система является системой с абсолютным приоритетом, то рассмотрение вопросов обслуживания заявок, обладающих приоритетом, можно проводить без учета наличия заявок, не обладающих приоритетом. Одноканальная система без ограничения мест в очереди была рассмотрена в главе 4. Следовательно,
(i
= 0, 1, 2, 3, …).
Для нахождения вероятностей Pi,j применим метод производящих функций [9] и введем в рассмотрение производящую функцию вида
.
Отметим некоторые свойства этой производящей функции:
1.
.
2.
.
3.
Среднее число заявок, не обладающих приоритетом и находящихся в системе, найдем так:
После этих предварительных замечаний найдем производящую функцию (x,y), для чего в уравнениях (5.1) примем все производные равными нулю. Далее первое уравнение системы (5.1) умножим на x0y0 = 1, второе уравнение – на xiy0 = xi, третье уравнение – на x0y j = y j, четвертое уравнение – на xiy j и все эти уравнения сложим, перебрав все возможные значения i и j. Проделав это и проведя некоторые простые преобразования, получим
+
(5.2)
Двойные суммы, входящие в выражение (5.2), могут быть выражены через функции (x,y). Проведя соответствующие преобразования выражения (5.2), получим следующую формулу:
.
Найдем
корни x1
и x2
знаменателя этого выражения, считая,
что 1
<
0:
,
.
Это дает возможность (после некоторых довольно громоздких преобразований, которые опускаем) получить следующее выражение для производящей функции:
,
где = 1+ 2.
Обратим внимание на то, что величина x1 зависит от переменной y. При у = 1 х1 = 1.
Для нахождения отдельных вероятностей состояний можно воспользоваться следующими формулами:
,
.
Воспользовавшись выражением производящей функции [9] для отыскания закона распределения числа заявок, не обладающих приоритетом в обслуживании и находящихся в СМО, получим
,
откуда
.
(5.3)
При вычислении производных по выражению (5.3) нужно иметь в виду, что величина х1 является функцией у.
Среднее число заявок, обладающих приоритетом в обслуживании и находящихся в очереди, определяется из выражения
Среднее время пребывания заявки, обладающей приоритетом, в системе (в очереди),
.
Среднее время пребывания заявки, обладающей приоритетом, в системе (в очереди и на обслуживании),
.
Среднее число заявок, не обладающих приоритетом и находящихся в системе,
При 1 = 2 получим
.
Среднее время нахождения в системе заявки, не обладающей приоритетом,
.
Среднее
время пребывания заявки, обладающей
приоритетом, в очереди
,
откуда среднее время ожидания в очереди для заявки, не обладающей приоритетом,
.
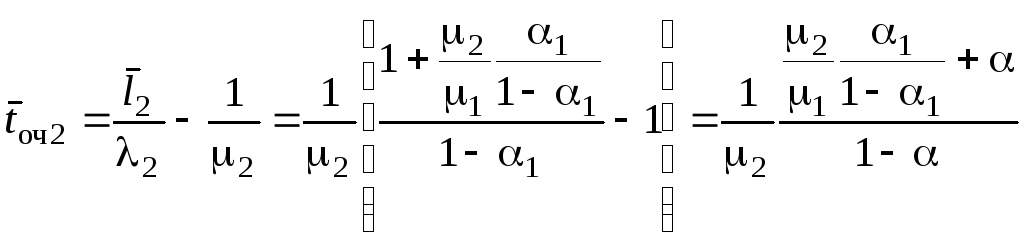