3.4.5. Примеры систем массового обслуживания с отказами

Пример 3.1. Рассматривается работа районной автоматической телефонной станции (АТС), которая обеспечивает не более 120 переговоров одновременно. Средняя длительность переговоров 1/μ = 1 мин. Вызовы на станцию поступают через 0,5 с, т.е. 1/λ = 0,5 с. Требуется найти характеристики работы АТС: ,,,,.

Решение

АТС представляет собой 120-канальную СМО с отказами. Параметры системы следующие: n = 120; λ = 2 сооб/с; μ = 1/60 сооб/с; ρ = λ/μ = 120.

Среднее число занятых каналов

= ρР_обс = ρ= 120≈ 120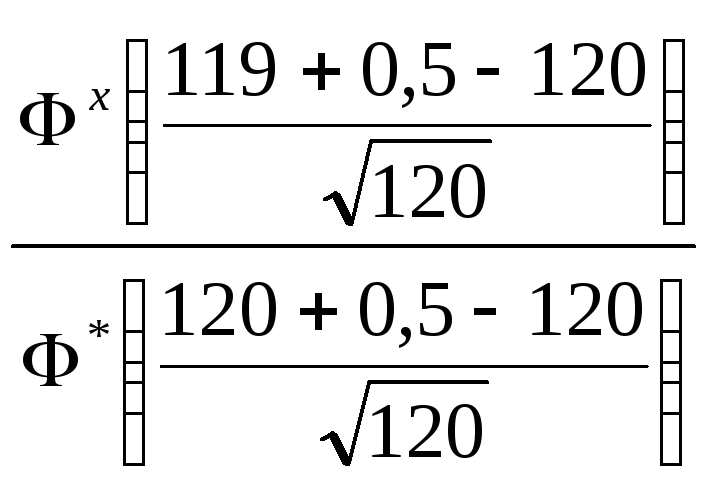≈ 112.

Вероятность обслуживания

Р_обс = /ρ =.

Вероятность занятости канала

=/n.

Среднее время занятости канала

= 1/μ = 1 мин = 60 с.

Среднее время простоя канала

= ≈ 4,5 с.

Пример 3.2. Обслуживание заявок производится СМО с отказами, параметрами системы n, λ, μ. Обслуживание каждой заявки приносит среднюю прибыль С₁. С целью увеличения доходов обслуживания предлагается провести реорганизацию, состоящую в том, что система будет допускать взаимопомощь между каналами. На преобразование СМО с отказами в СМО с отказами и взаимопомощью требуется израсходовать стоимость С₂. Переоборудование занимает время τ_п. Определить, по истечении какого срока времени t после начала преобразования вновь организованная СМО с отказами и взаимопомощью начнет приносить прибыль.

Решение

Задачу будем решать при условии, что время установления стационарного режима в системах мало по сравнению со временем переоборудования τ_п и временем t (t > τ_п). Начало отсчета для времени τ_п и t одно. В этом случае можно записать следующее уравнение:

С₁λ₀⁽¹⁾ t = –С₂ + С₁ λ₀⁽²⁾( t – τ_п),

где ₀⁽¹⁾ = – абсолютная пропускная способность СМО с отказами; λ₀⁽²⁾ = – абсолютная пропускная способность СМО с отказами и взаимопомощью; ρ = λ/μ; χ = λ/nμ.

Решая это уравнение, получим t, по истечении которого реорганизация начнет приносить прибыль:

.

Пример 3.3. Определить, насколько увеличится вероятность обслуживания для СМО с отказами, имеющей следующие параметры: n = 10, λ = = 8 сооб/мин; μ = 0,8 сооб/мин, если обеспечить взаимопомощь группы из двух каналов (l = 2).

Решение

Для СМО с отказами без взаимопомощи вероятность обслуживания

Р_обс⁽¹⁾ = .

Для примера

Р_обс⁽¹⁾ = = 0,795.

Для системы с частичной взаимопомощью имеем

N = 10; χ = λ / nμ = 1; ρ_l = λ / lμ = 0,5; h = ]n / l[ = 5.

Для этой системы в случае, когда χ = 1, вероятность обслуживания

Р_обс⁽²⁾ = = 0,883.

Таким образом,

Р_обс⁽²⁾ – Р_обс⁽¹⁾ = 0,883 – 0,795 = 0,088.

Пример 3.4. Рассматривается система ПВО с нарушенным управлением. Нарушение управления состоит в том, что каждую влетающую в зону обстрела цель обстреливают все свободные к этому времени каналы. Обстрел цели каждым каналом длится случайное время, распределенное по показательному закону с параметром . За это время каждый канал поражает цель с вероятностью р независимо от других каналов, принимающих участие в обстреле. Определить характеристики работы системы, если параметры системы ПВО следующие: n = 4;  = 4 1/мин;  = 1 1/мин;  = = 0,5.

Решение

В рассматриваемом примере величина – целое число. Вероятности различных состояний системы следующие:

; ;

;;

.

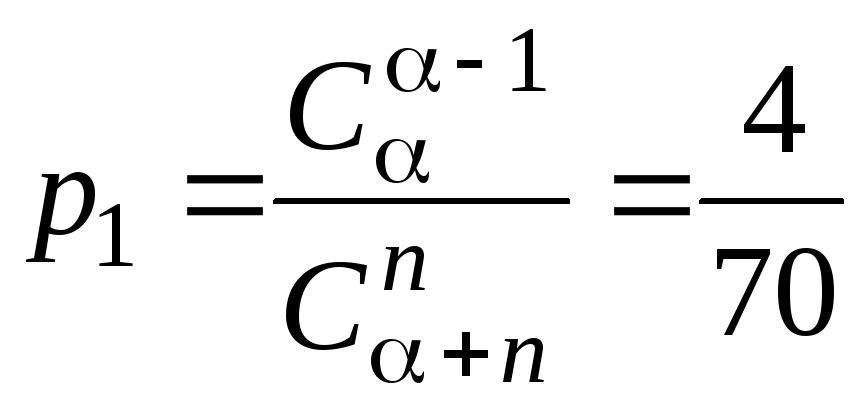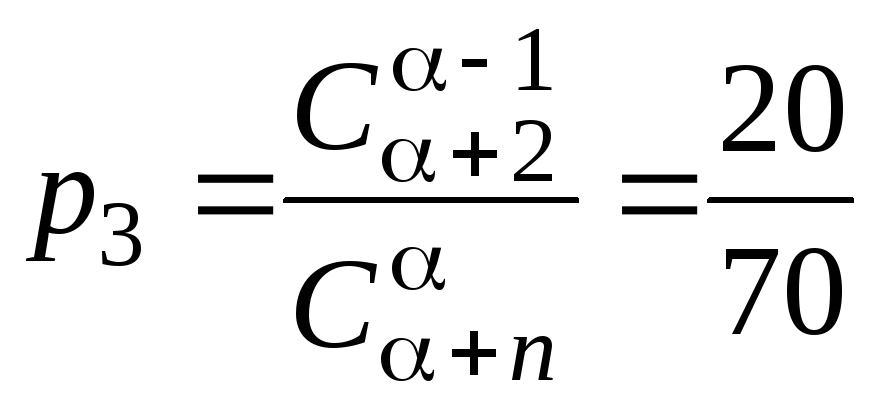Вероятности поражения цели

.

Вероятность полной загрузки системы

.