2. Модель Джулии

      Модель фрактала Джулии  имеет   то же уравнение, что и модель Мандельброта: Z=Z²+c,    только  здесь    переменным параметром является не  c,   a  z.

Соответственно, меняется вся структура фрактала, так как теперь на начальное положение  не накладывается никаких ограничений.   Между  моделями Мандельброта и Джулии существует такое различие: если модель Мандельброта  является статической ( так как z начальное всегда равно нулю), то модель Джулии является динамической моделью    фрактала.   На рис. 4  показано графическое представление фрактала Джулии.

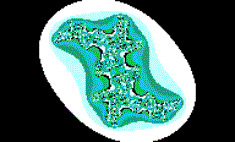
Рис. 4 Модель Джулии

       Как видно из рисунка фрактала, он симметричную относительно центральной точки форму, тогда как  фрактал Мандельброта имеет форму, симметричную относительно  оси.

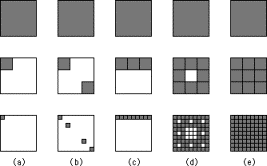
3. Ковер Серпинского

       Ковер Серпинского считается еще одной моделью  фрактала. Строится он  следующим образом: берется  квадрат, делится на девять квадратов,    вырезается центральный квадрат.  Затем  с каждым из восьми  оставшихся квадратов проделывается подобная процедура. И так до бесконечности.   В результате вместо  целого квадрата мы получаем ковер со своеобразным симметричным рисунком.  Впервые данную модель предложил математик Серпинский, в честь которого он и получил свое название.   Пример ковра Серпинского можно увидеть на рис. 4d.

  

Рис.4 Построение ковра Серпинского

4. Кривая Коха

     В начале  ХХ века математики  искали   такие кривые, которые ни в одной точке не имеют  касательной.  Это означало, что кривая резко меняет свое направление, и притом с колоссально   большой скоростью (производная равна бесконечности).  Поиски данных кривых были вызваны не просто праздным интересом математиков. Дело в том, что  в начале ХХ  века очень бурно развивалась   квантовая механика.  Исследователь М.Броун    зарисовал  траекторию движения взвешенных частиц в воде и  объяснил это явление так:  беспорядочно движущиеся атомы жидкости ударяются  о взвешенные частицы и тем самым приводят их в движение.  После такого объяснения броуновского движения перед учеными встала задача найти такую кривую, которая   бы наилучшим образом аппроксимировала  движение броуновских частиц.   Для  этого кривая должна была отвечать следующим свойствам:  не иметь касательной  ни в одной точке.  Математик Кох предложил  одну такую кривую. Мы не будем вдаваться в  объяснения правила ее построения, а просто приведем ее изображение, из которого все станет ясно (рис.5).

Рис.5  Этапы построения кривой Коха

       Кривая Коха является еще одним примером фрактала, так как   каждая ее часть является уменьшенным изображением всей кривой.

6. Графические изображения различных фракталов

Рис. 6  Примеры  графического представления фракталов

Фракталы в природе 

Множество процессов, происходящих в природе и обществе – от космических до социальных и физиологических, – характеризуется хаотической фрактальной динамикой. Фрактальность природных объектов подтверждается возможностью построения весьма правдоподобных компьютерных ландшафтов виртуального мира на основе простых фрактальных программ, в которых приближение к реальности достигается некоторой степенью нерегулярности путем введения случайных чисел. Морфогенез растений также успешно имитируется подобными программами. Моделирование морфогенеза животных на всех уровнях их организации – динамично развивающаяся область биологии. Биологические структуры сложной пространственной организации могут быть количественно охарактеризованы путем определения фрактальной размерности, служащей показателем морфологической сложности этих структур. Вовлечением фрактальных алгоритмов в биологический морфогенез обеспечивается сжатое генетическое кодирование. Фракталоподобные структуры живой природы характеризуются ограниченной шкалой повторов и менее хаотизированы по сравнению с фракталами неживой природы; как правило, это мультифракталы, т.е. неоднородные фракталы.

Культура

Использование подходов фрактальной геометрии позволяет выявить сходство ряда живых и неживых объектов – как природных, так и созданных человеком. Один из примеров такого параллелизма формообразования дает сопоставление конструкций геодезических куполов с организацией молекул фуллеренов, макромолекулярных комплексов клеток многоклеточных животных и скелетных структур радиолярий. Строительные конструкции геодезических куполов были запатентованы в 1954 г. Р.Б.Фуллером (1895–1983), американским изобретателем, архитектором и философом; в нашей стране такими разработками занимался М.С.Туполев. Геодезические купола могут быть образованы сложной сетью треугольников, которые формируют поверхность, близкую к сферической. Повторные подразделения на треугольники, характерные для геодезических куполов, образуют фрактальный алгоритм. Конструкции с таким триангуляционным разбиением оказались не только перспективными в архитектуре, но и очень сходными с природными формами.

В 90-е годы прошлого века было получено новое вещество – фуллерит, состоящее из молекул углерода, фуллеренов (этимология названий фуллеренов и фуллерита весьма прозрачно связана с именем Фуллера). Фуллериталлотропная модификация углерода, третья кристаллическая форма углерода (две ранее известные формы – графит и алмаз). Молекулы фуллеренов представляют собой замкнутую поверхность в форме сферы или сфероида, на которой располагаются атомы углерода. Конструкции геодезических куполов подобны и некоторым биологическим структурам, например макромолекулярным комплексам

клатрина, сети пучков актиновых филаментов клеток многоклеточных животных и скелетам некоторых радиолярий, одноклеточных организмов.

Математическая теория фракталов

Как построить математическую модель таких объектов с определенной степенью подробности описания их геометрической формы?

Вообще, всякая математическая модель есть некоторая абстракция, отражающая выбранные существенные свойства рассматриваемых реальных объектов, процессов (физических ситуаций). В результате процедуры выделения и формализации (выражения содержания изучаемого явления через знаковые формы – символы, знаки, термины, буквенные обозначения и др.) получают математическое описание явления, т. е. его математическую модель, которую далее можно исследовать математическими методами как математическую задачу, математическую проблему. Формализация позволяет производить логические умозаключения (выводы), вычислительные операции, исследования структуры, обращаясь непосредственно со знаковыми формами (с формулами, геометрическими построениями, логическими суждениями), абстрагируясь от конкретного содержания явления.

Использование математических моделей (и результатов исследований этих моделей) происходит на основе их интерпретации в реальных ситуациях. При этом использование будет оправданным (правомерным) и эффективным, если модель будет достаточно адекватной, а полученные математические результаты практически реализуемы. Для понимания некоторого данного явления (на основе его математического описания) математика вырабатывает, подобно обычному языку, метафоры (образные представления), позволяющие объяснить это явление, ставя ему в соответствие другое явление, более привычное или воспринимаемое как таковое.

Фракталы представляют собой математические модели сложных структур, пространственное изображение которых представляется в виде сломанных, морщинистых и нечетких форм. Фракталы (как математические абстракции) обладают следующими характерными свойствами, отображающими их иррегулярную сущность: 

• самоподобие (иерархический принцип организации);

• способность к развитию (принцип непрерывности формообразования);

• дробная метрическая размерность (принцип сингулярности меры);

• размытость, нечеткость контуров (принцип неопределенности границ);

• геометрическое представление хаотической динамики (принцип динамического хаоса).

Фрактальные структуры (с перечисленными характерными свойствами) имеют широкое распространение, как в естественной, так и в искусственной средах.

Рассмотрим характерные свойства фракталов с позиций процесса формообразования и визуального представления.

Самоподобие

Самоподобие в математических алгоритмах реализуется с помощью рекурсивных процедур. Вообще, рекурсия – способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Преимущество рекурсивного определения объекта (действия) заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов (действий, итераций), бесконечную итерационную процедуру (вычислений, построений) действий. Практически все геометрические фракталы задаются в форме бесконечной рекурсии.

Пространственная форма фрактала повторяется (повторяет себя) в каждом фрагменте в любом масштабе. Его структура отражает иерархический принцип организации материи в природе. При увеличении масштаба видимая структура не упрощается, на всех шкалах проявляется одинаково сложная картина.

Способность фрактальных структур к развитию определяет непрерывность процесса формообразования, незавершенность пространственного представления фрактала на каждом текущем шаге итерационного процесса построения. Фрактал никогда не бывает законченным.

Фрактал есть итоговый результат бесконечной процедуры, т. е. является бесконечным в развитии. Нельзя изобразить бесконечность процесса, нельзя реально выполнить бесконечную рекурсивную процедуру. Это можно только мыслить. Поэтому всякое наглядное представление фрактала – это на самом деле изображение квазифрактала (некоторого приближения искомого фрактала), определяется конечной процедурой (процесс построения останавливается на каком-то конечном шаге). При некотором большом масштабе его фрактальная структура исчезает (т. е. отсутствует повторение базовой формы в уменьшенном виде, начиная с некоторого уровня, определяющего степень уменьшения).

Размерность

Математическое понимание фрактала определяет его как множество с дробной размерностью. Дробное значение фрактальной размерности характеризует степень заполнения пространства фрактальной структурой, тогда как значение лакунарности представляет собой меру неоднородности структуры фрактала. Количественная характеристика структур сложной пространственной организации через фрактальную размерность может служить показателем морфологической сложности этих структур. Таким образом, определяется природный морфогенез (сложная пространственная организация природных (естественных) форм) в сопоставлении с фрактальными структурами. Следует заметить, что архитектурные формы более регулярны, чем природные, включают меньшее число повторов с их вариациями.

Вообще, понятие размерности можно определять по-разному (т. е. для одних и тех же множеств, объектов можно определить не одну, а несколько различных размерностей). Необходимость рассмотрения разных размерностей следует из топологической сложности объектов. Обычно размер кривой оценивается ее длиной, размер поверхности – ее площадью, размер трехмерного тела – его объемом. Для фрактальной структуры такой подход не годится. Например, длина простейшего фрактала – канторового множества – равна 0, а длина снежинки Коха (непрерывная замкнутая кривая, ограничивающая конечную площадь) равна бесконечности. В то же время метрическая размерность канторового множества (или размерность в смысле Хаусдорфа – хаусдорфова размерность) равна ln2/ln3 ≈ 0,63, а метрическая размерность снежинки Коха равна ln4/ln3 ≈ 1,26. Квадратный ковер Серпинского имеет хаусдорфову размерность ln8/ln3 ≈ 1,89 (и, в частности, имеет нулевую меру Лебега – нулевую площадь).

Размерность Хаусдорфа – естественный способ определить размерность множества в метрическом пространстве и вполне согласуется с нашими обычными представлениями о размерности в случае регулярных (гладких) множеств. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой – единице, размерность гладкой поверхности – двум и размерность множества ненулевого объёма – трём. Для фрактальных множеств (отражающих негладкие многообразия, имеющие нерегулярную структуру) размерность Хаусдорфа может принимать дробные значения.

Граница фрактальной фигуры не определяется из ее визуального представления: увеличивая изображение фрактала, получаем невидимые до этого подробности, состоящие из элементов, повторяющих в малом масштабе саму фигуру. И так, в принципе, до бесконечности.

Для анализа закономерностей, присущих системам, которые могут казаться непредсказуемыми и абсолютно хаотическими, используются фрактальная геометрия и математика хаоса. При этом возможно описание траекторий хаотических систем через геометрические фракталы, т. е. геометрическое представление хаотической динамики.

Динамический хаос – это явление в теории динамических систем, при котором поведение нелинейной системы выглядит случайным, хотя подчиняется детерминистическим законам. Причиной появления хаоса является неустойчивость по отношению к начальным условиям и параметрам: малое изменение начального условия со временем приводит к сколь угодно большим изменениям динамики системы.

Анализ поведения динамической системы осуществляется с помощью аттрактора – множества состояний этой системы, к которому она стремится с течением времени (т. е. множество точек притяжения фазового пространства). Хаотичная динамика характеризуется странными (нерегулярными) аттракторами, часто имеющими фрактальную структуру.

Примеры применения фракталов в архитектуре

Применение фрактальных правил построения широко распространено и в архитектуре. Фрактальная архитектура делится на два типа: искусственно созданная и естественно сложившаяся. В свою очередь, искусственно созданная фрактальная архитектура бывает интуитивной и сознательной. Под интуитивной фрактальностью подразумевается структура многих шедевров мировой архитектуры прошлого, в которых архитектор или строители неосознанно использовали фрактальные принципы. При этом фракталоподобные формы представлены в сооружениях разных эпох и народностей, отражают различные алгоритмы формообразования. Б. Мандельброт первым написал о фрактальности архитектуры, указав для сравнения форму здания Парижской оперы. В [3, 4] приводится ряд примеров фрактальных форм в архитектуре. Это самоподобие форм в архитектуре зданий Исторического музея (Москва); почтамта (Владивосток); индийских храмов (комплекс в Кхаджурахо); фрактальные прообразы и архитектура пирамидальных фасадов (ступенчатые пирамиды), колоколен, фасадов готических зданий Германии. Замок Кастель-дель-Монте, Италия (построен по собственному проекту императором Священной Римской империи Фридрихом II), представляет в плане правильный восьмиугольник, к вершинам которого пристроены восемь башен, также имеющих в плане форму правильных восьмиугольников. Математическая метафора в виде графика функции Вейерштрасса представляется прообразом для силуэта храмов с множеством вертикальных повторяющихся элементов (силуэт Миланского собора). Расположение и размеры куполов многоглавых церквей, условно показанные в одной плоскости плана с осевой симметрией, также имеют прообразом фрактальную структуру (типа «салфетки» Серпинского с кругами). Спиралеподобные формы, отражающие один из распространенных фрактальных алгоритмов в природе, используются и в искусственной среде, включая архитектуру и дизайн (спиральный декор храма Василия Блаженного, металлические узоры оград и решеток, произведения декоративно-прикладного искусства).

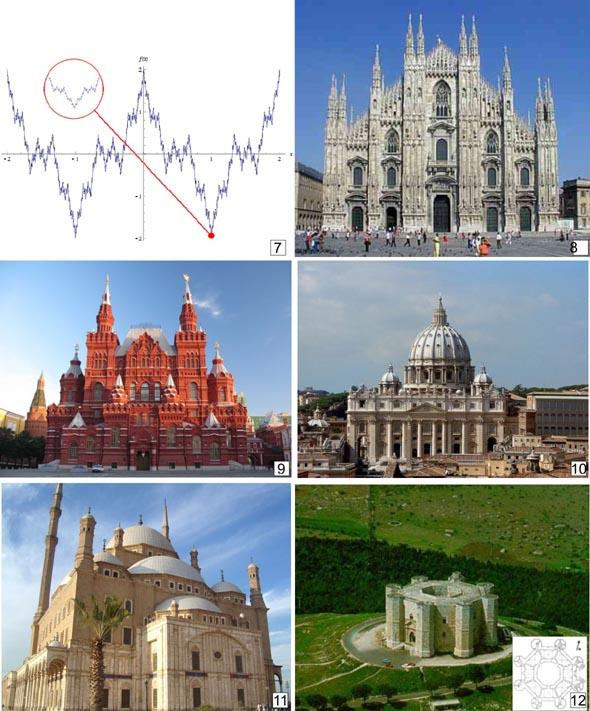
Фрактальность архитектурных форм:  1) Спасская башня, Кремль, Москва 2) Парижская опера 3) Собор Василия Блаженного, Москва 4) Храм в Кхаджурахо, Индия 5) Собор Саграда Фамилия (, Фасад Страстей, Барселона (Испания)6) Мост Тауэр, Лондон 7) Функция Вейерштрасса;  8) Кафедральный собор в Милане);   9) Исторический музей, Москва 10) Собор Святого Петра, Рим, Ватикан 11) Мечеть Мухаммада Али в каирской Цитадели 12) Замок Кастель-дель-Монте и план замка, Италия.

Многие исследователи данной темы говорят об интуитивной фрактальности в архитектуре. Т.е. в некоторых шедеврах мировой архитектуры прошлого архитектор неосознанно создавал фрактальные системы. Яркими примерами такой архитектуры являются готические соборы Средневековья, работы Антонио Гзуди, Фрэнка Ллойда Райта и др.

В примерах сознательной фрактальности архитектуры проектировщик намеренно закладывал в основу проекта сформулированные математиками фрактальные принципы (работы Питера Эйзенмана , LAB Architecture studio, Д. Либескинда,

ARM, Morphosis, Френка Гэри, Гоега Линна, группы LAB, Брэйтса Смарта и др.).

Еще один интересный пример фрактальности в архитектуре, который я выделила это группа «блобмайстеров». Полигоны (или же фракталы) в их проектах приобрели устойчивое толкование: отныне они - не просто компьютерный способ построения формы, а сложная пространственно-математическая игра. Так появилась топологическая или нелинейная поверхность. В этом случае архитекторы стремятся избавиться от плоскостей - они создают сложные гладкие поверхности, представление о свободном пространстве, не имеющем углов, ровных плоскостей. Нелинейная поверхность, переходя от одного проекта к другому, теряет свою складчатость и стремится захватить все здание целиком. Вершиной этой тенденции и является Bubie (пузырь) или Blob (капля). Суть его в том, что здание или же часть комплекса покрывается со всех сторон нелинейной поверхностью и как будто парит в воздухе. Проекты очень разные, но формальная структура у них одинакова, это не шар; для «пузыря» принципиально важны асимметричные, нелинейные очертания, фактически это «жемчужина неправильной формы», порождение электронного барокко конца двадцатого века.

Хочу отметить также «лично» архитекторов, использующих фракталы. Даниэль Либескинд - один из ведущих архитекторов в мире. Его архитектуре сложно дать определение: формально - это пост-структурапизм и деконструктивизм: асимметрия, сложные переплетения осей, парадоксальные сочетания пространств. Но его проекты нельзя заключить в рамки одного стиля, даже очень широкие. Его архитектура не похожа на привычную, она выглядит как авангардная инсталляция (жилой комплекс Reflections, Сингапур, жилой комплекс «Ascent» Ковингтон, США, корпус Фредерика С. Хэмилтона Денверского музея искусств). Фостер же увлечен идеей экологичности и очень внимателен к новациям в области энергосбережения. Свои идеи архитектор стремится воплотить с максимальным использованием естественного света и воздуха, привлекая для этой цели самые смелые инженерные решения. Спроектированные им здания сами регулируют потоки воздуха и света, активно экономя энергию (здание Шанхайского банка, Millennium Bridge в Лондоне, крупнейший аэропормира в Пекине, одна из самых оригинальных построек Лондона - небоскреб~«огурец» ).

Заключение Фрактальная теория влияет на умы авторов, ориентирует творческий процесс. В архитектурной и градостроительной деятельности зачастую фракталы применяются на уровне эмоционально-чувственного восприятия, они дают «творческий импульс, направляющий мысль архитектора или градостроителя в определенном направлении». Фракталы объединяют в себе массу образов: «цветовые тона, мелодические сочетания, линии». Таким образом, происходит интеграция эмоционального и рационального.  Фрактал нужно рассматривать прежде всего, как форму, позволяющую создавать уникальные решения в области архитектуры и градостроительства.  Фрактальные структуры отвечают всем требованиям архитектурной композиции. Исходя из законов построения фрактальной структуры можно предугадать, как будет воздействовать реальный объект, построенный по законам данного фрактала на чувственно-эмоциональное восприятие зрителя. «В аспекте представления об организации и существования архитектуры как динамической знаковой системы, опираясь на фрактальные принципы, можно говорить об архитектурной текстуальности как о принципе организации порядка в хаосе». Благодаря исследованию фрактальных структур появлялись первые операциональные способы работы с ними, например, появилась методология, связывающая в целое представление таких, казалось бы, совершенно не корреспондирующих между собой объектов, как фрактал и генеральный план города.  Нужно отметить, что создание каких-либо концепций при помощи фрактальной теории – это в какой-то мере создание «идеальных типов». При их помощи гораздо легче перенестись на реальность. Создается «идеальная» модель, которая служит основой для исследования. В результате возникают определенные пути решения поставленных задач, которые внедряются в существующую ситуацию или по которым создается новая действительность.  «Со времени возникновения фрактальной теории прошло не более трети века, но за это время фракталы дали мощный концептуальный импульс для многих современных архитекторов. Возможно, первоначальное увлечение фракталами и было слишком бурным, однако нам представляется бесспорным право архитектора на свой язык и свою, пусть и адаптированную, интерпретацию образов, право выстраивать свою теорию, переводя заимствованные из других областей понятия в метафорический смысл».

Таким образом, складывается на сегодняшний момент ситуация, которую синергетика называет бифуркацией: перед каждым, кто входит в мир науки, открывается необходимость и возможность выбора своей методологической ориентации. Важно отметить то, что существует на сегодняшний день практика применения фрактальной теории в различных сферах человеческой деятельности, в частности архитектуре и градостроительстве. Симбиоз математики и архитектуры переводит развитие фрактальной теории в архитектуре и градостроительстве на новый уровень.

24