7. Структурный синтез автомата

Выберем в качестве структурной схемы распознающего автомата следующую схему:

Рис. 5. Структурная схема распознающего автомата

Схема (рис. 5) состоит из комбинационной схемы, реализующей функцию возбуждения элементов памяти. Элементы памяти построены из триггеров по двухрегистровой схеме. Схема содержит также дешифратор входных сигналов.

При синхронной реализации автомата предполагается, что все переходные процессы в этих схемах успевают закончиться к моменту прихода сигнала t1, стробирующего (разрешающего) прием информации с выходов комбинационной схемы в триггеры регистра 1. Второй триггерный регистр, прием информации в который стробируется синхросигналом t2, нужен для того, чтобы все состояния автомата сделать устойчивыми. Триггеры регистра 1 будем называть вспомогательными, а регистра 2 - основными.

derr - сигнал функции ошибки; dok - сигнал функции принадлежности цепочки входных символов языку с грамматикой G’, (p1, p2, p3 - код входного символа); z(t-1) - код предыдущего состояния; z(t) - код нового состояния

С помощью сигнала НУ осуществляется начальная установка триггеров автомата.

Дешифратор преобразует двоичный код символов (p1,p2,p3) в унитарный код, в котором только одна из выходных переменных принимает значение 1, в то время как все другие равны 0.

Комбинационная схема автомата реализует функцию его переходов. Исходным заданием для ее построения является таблица или граф переходов, а также выбранный вариант кодирования .

Построить функцию переходов, значит найти переключательную функцию кодирующих (внутренних) переменных. Каждая внутренняя переменная кода (z1,z2,z3,z4 ) представляет собой состояние соответствующего элемента памяти, то есть триггера. По переключательным функциям внутренних переменных находятся функции возбуждения соответствующих им триггеров. Реализация этих функций образует комбинационную схему автомата.

Рассмотрим часть общей комбинационной схемы автомата, реализующую функцию переходов по x0, x1, ..., x7.

Рис. 6. Общая комбинационная схема автомата

Рассмотрим построение логической схемы 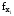на примере для f(x0):

z(t)

xo f(xo) z(t+1)

Рис. 7. Общий вид схемы обработки сигнала х₀

Пусть входной сигнал xo обрабатывается автоматом в соответствии с функцией переходов следующим образом: r1  r2; r2  r11. Приведем таблицу кодировки (см. табл.8), чтобы на ее основе построить таблицу переходов автомата по символу xo.

Таблица 8

r0	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10	r11
0000	0010	0110	0001	1000	1100	1010	1001	0011	0111	0101	0100

Cоставим таблицу переходов автомата по символу x0:

Таблица 9

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r1	0	0	1	0	0	1	1	0
r2	0	1	1	0	0	1	0	0

Запишем в соответствии с табл.9 функции z(t+1). Будем иметь:

z1(t+1) = z1(t); z2(t+1) = z3(t);

z3 (t+1) = 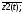z4(t+1) = z1(t);

Построим схему на элементах И-НЕ:

Рис. 8. Схема обработки входного сигнала х₀

Аналогично составляются логические функции остальных z_i (t+1)

и строятся соответствующие им комбинационные схемы f_xi , а в итоге и вся схема : x_i & z (t)  z (t+1) , то есть схема таблицы переходов автомата. В случае, когда по таблице переходов сложно записать функцию z_i(t+1), применяют построение карт Карно и минимизацию слабо определенных функций.

Cоставим таблицу переходов автомата по символу x1:

Таблица 10

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r3	0	0	0	1	1	0	0	1
r9	0	1	1	1	0	1	0	0

Запишем в соответствии с табл.10 функции z(t+1). Будем иметь:

z1 (t+1) = z3(t+1) = z1(t);

z2(t+1) = z2(t); z4 (t+1) =

Построим схему на элементах И-НЕ:

Рис. 9. Схема обработки входного сигнала х₁

Cоставим таблицу переходов автомата по символу x2:

Таблица 11

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r6	1	0	1	0	0	0	1	0
r7	1	0	0	1	0	0	1	1

Запишем в соответствии с табл.11 функции z(t+1). Будем иметь:

z1 (t+1) = z2(t); z3(t+1) =

z2(t+1) = z2(t); z4 (t+1) = z4 (t);

Построим схему на элементах И-НЕ:

Рис. 10. Схема обработки входного сигнала х₂

Cоставим таблицу переходов автомата по символу x3:

Таблица 12

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r11	0	1	0	0	0	0	0	0

Запишем в соответствии с табл.12 функции z(t+1). Будем иметь:

z1 (t+1) = z1(t); z3(t+1) = z1 (t);

z2(t+1) = z1(t); z4 (t+1) = z1 (t);

Построим схему на элементах И-НЕ:

Рис. 11. Схема обработки входного сигнала х₃

Cоставим таблицу переходов автомата по символу x4:

Таблица 13

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r0	0	0	0	0	0	1	0	0
r1	0	0	1	0	0	1	0	0
r2	0	1	1	0	0	0	0	0
r3	0	0	0	1	1	0	1	1
r4	1	0	0	0	1	1	0	0
r5	1	1	0	0	0	0	1	0

Запишем в соответствии с табл.13 функции z(t+1). Будем иметь:

z1 (t+1) =;z3(t+1) =

z2(t+1) = z4 (t+1) =

Построим схему на элементах И-НЕ:

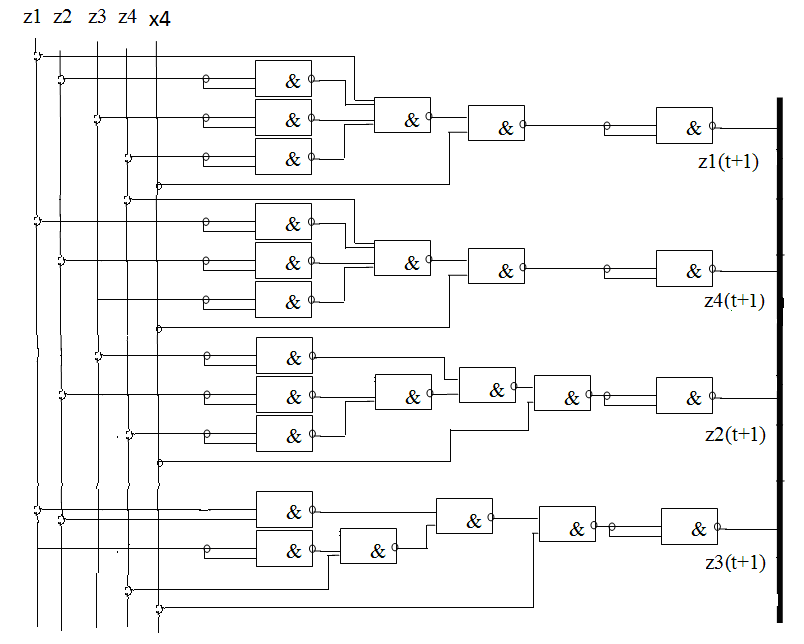
Рис. 12. Схема обработки входного сигнала х₄

Cоставим таблицу переходов автомата по символу x5:

Таблица 14

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r0	0	0	0	0	0	0	1	0
r8	0	0	1	1	0	1	1	1

Запишем в соответствии с табл.14 функции z(t+1). Будем иметь:

z1 (t+1) = z1(t); z3(t+1) =

z2(t+1) = z3(t); z4 (t+1) = z3 (t);

Построим схему на элементах И-НЕ:

Рис. 13. Схема обработки входного сигнала х₅

Cоставим таблицу переходов автомата по символу x6:

Таблица 15

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r0	0	0	0	0	0	1	0	0
r3	0	0	0	1	0	1	0	1
r4	1	0	0	0	1	0	1	0

Запишем в соответствии с табл.15 функции z(t+1). Будем иметь:

z1 (t+1) = 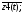z3(t+1) = z1(t);

z2(t+1) = z4(t); z4 (t+1) = z4 (t);

Построим схему на элементах И-НЕ:

Рис. 14. Схема обработки входного сигнала х₆

Cоставим таблицу переходов автомата по символу x7:

Таблица 16

ri	t				t+1
	z1	z2	z3	z4	z1	z2	z3	z4
r0	0	0	0	0	0	0	0	1
r10	0	1	0	1	0	1	1	1

Запишем в соответствии с табл.16 функции z(t+1). Будем иметь:

z1 (t+1) = z1(t); z3(t+1) = z2(t);

z2(t+1) = z2(t); z4 (t+1) =

Построим схему на элементах И-НЕ:

Рис. 15. Схема обработки входного сигнала х₇

Функция возбуждения сигнала ошибки может быть представлена в виде:

derr = x0  derr_x0  x1 & derr _x1  ...  x7 & derr _x7.

Считаем, что ошибки по x_i могут возникать тогда, когда на x_i сработало какое-либо другое состояние, не соответствующее заданному по таблице переходов. Другими словами, при приходе сигнала x_i автомат находился не в тех состояниях, которые ему были предписаны таблицей переходов. Построим соответствующую таблицу:

Таблица 17

	r	¬derr x0	¬derr x1	¬derr x2	¬derr x3	¬derr x4	¬derr x5	¬derr x6	¬derr x7
0	0000	0	0	0	0	1	1	1	1
1	0010	1	0	0	0	1	0	0	0
2	0110	1	0	0	0	1	0	0	0
3	0001	0	1	0	0	1	0	1	0
4	1000	0	0	0	0	1	0	1	0
5	1100	0	0	0	0	1	0	0	0
6	1010	0	0	1	0	0	0	0	0
7	1001	0	0	1	0	0	0	0	0
8	0011	0	0	0	0	0	1	0	0
9	0111	0	1	0	0	0	0	0	0
10	0101	0	0	0	0	0	0	0	1
11	0100	0	0	0	1	0	0	0	0

Анализ табл. 17 показывает, что в ней больше нулей, чем единиц. Поэтому по ней удобно строить логическую функцию для . Для каждой функциипроводим минимизацию слабо определенной функции. Затем берется отрицание полученной в ходе минимизации функции. Запишем функции ошибок при обработкеx0, x1 и т.д.:

Для x0:

(¬z1 ¬z2 z3 ¬z4) v (¬z1 z2 z3 ¬z4) = (¬z4 ¬z1 z3)& (¬z2 v z2) = ¬z4 ¬z1 z3

¬

Для x1:

(¬z1 ¬z2 z3 z4) v (¬z1 ¬z2 ¬z3 z4) = (¬z1 ¬z2 z4) & (z3 v ¬z3) = ¬z1¬ z2 z4

¬

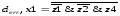
Для x2:

(z1 ¬z2 z3 ¬z4) v (z1 ¬z2 ¬z3 z4)

¬

Для x3:

¬

Для x4 проведём минимизацию при помощи карты Карно:

(¬z1 ¬z4) v (z1 ¬z4) v (z4 ¬z2 ¬z3 ¬z1) = ¬z4 (z1 v ¬z1) v (z4 ¬z1 ¬z2¬z3) = ¬z4 v (¬z1 ¬z2 ¬z3 z4)

¬

Для x5:

(¬z1 ¬z2 ¬z3 ¬z4) v (¬z1 ¬z2 z3 z4)

¬

Для x6 проведём минимизацию при помощи карты Карно:

(¬z3 ¬z2) v (¬z3 ¬z4 z1) = ¬z3 (¬z2 v ¬z4 z1)

¬

Для x7:

(¬z1 ¬z2 ¬z3 ¬z4) v (¬z1 z2 ¬z3 z4)

¬

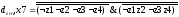
Функцию ошибки можно представить формулой вида

=

которая после формирования необходимых логических функций будет изображаться соответствующей комбинационной схемой.

Сигнал dok=1 вырабатывается только тогда, когда на вход автомата пришел сигнал «конец цепочки», в рассматриваемой задаче x3, а автомат находился в заключительном состоянии, то есть

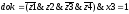
Очевидно, при этом ¬ derr = 1.

Комбинационная схема функции dok строится аналогично рассмотренным выше построениям.