13 Множественная регрессия

Множественная регрессия – это аппроксимация зависимости СВ от нескольких независимых переменных величин. Исходными данными является набор векторов , которые сопоставляют значениямнезависимых переменныхзначение зависимой переменнойдля каждого изэлементов выборки. Уравнение регрессии имеет вид

,

а ее построение сводится к определению таких значений коэффициентов , при которых достигается минимум одного из критериев, указанных в п.13.

Приведем соответствующие оптимизационные математические модели.

Оптимизация по критерию минимума максимальной ошибки.

При оптимизации по абсолютной величине ошибки

.

.

При оптимизации по относительной величине ошибки

,

Оптимизация по критерию минимума средней ошибки.

При оптимизации по абсолютной величине ошибки

,

При оптимизации по относительной величине ошибки

.

.

Эти задачи также являются задачами линейного программирования и решаются с помощью надстройки «Поиск решения» Excell.

Оптимизация по критерию минимума среднеквадратичной ошибки.

В случае оптимизации по абсолютной или относительной ошибке среднее квадратичное отклонение рассчитанных значений зависимой переменной от заданных равно соответственно

,

.

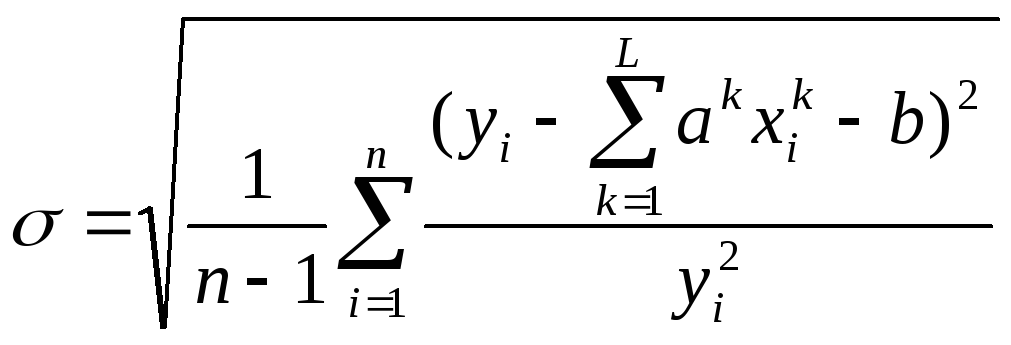Определение значений коэффициентовцелесообразно вести непосредственной оптимизацией вExcellсоответственно функций

,

.

Заметим, что это задачи нелинейной оптимизации, которые решаются с помощью надстройки «Поиск решения» Excell, но более сложны для решения.

14 Выделение наиболее значимых независимых переменных и их комплексов

Для того, чтобы определить, какая из независимых переменных или их группа наиболее существенно влияет на зависимую переменную при построении множественной регрессии, нужно в модели, описанные в п.13, внести следующее дополнение. Добавим к числу оптимизируемых коэффициентов двоичные неопределенные переменные , которые могут принимать значения 0 или 1, и в число ограничений на допустимые значения всех оптимизируемых коэффициентов включим следующие:

, (5)

где - количество независимых переменных, которые мы желаем учитывать при построении регрессии, а«очень большое» число, которое заведомо превосходит возможные значения неопределенных коэффициентов в уравнении регрессии.

Дополненная таким образом оптимизационная задача решается с помощью надстройки «Поиск решения» Excell. Напомним, что при этом нужно не забыть объявить переменныекак «двоичные». Тогда приоптимальное решение будет включать лишь одну, наиболее значимую независимую переменную, при- лишь две и т.д. Сопоставляя полученное при этом значение критерия с его значением при учете всех независимых переменных, можно увидеть, насколько учет лишь нескольких из них ухудшает результат.