§ 47. Реализация графической последовательности с максимальной связностью

В зависимости от выбора ведущих вершин l-процеду­ра может строить различные реализации графической последовательности. Ее можно организовать так, чтобы она строила реализации с некоторыми предписанными свойствами, если, конечно, такие реализации существу­ют. Ниже показано, как с помощью l-процедуры постро­ить такую реализацию G графической последовательности, число λ(G) реберной связности которой максималь­но среди всех реализаций.

Пусть d — правильная графическая n-последовательность. Поскольку λ(G)≤ δ(G) для любого графа G (δ(G)—минимальная степень вершин), то мы стремимся построить реализацию G последовательности d с λ(G)=d_n.

Вначале построим просто связную реализацию.

Теорема 47.1.Правильная графическая п-последователъностъ d может быть реализована связным графом тогда и только тогда, когда d_n > 0 и верно неравенство

Если указанные условия выполняются, то 1-процедура, на каждом шаге которой ведущей является вершина с минимальной положительной меткой, приводит к связ­ному графу.

Замечание. При d_n > 1 неравенство (1) выполня­ется автоматически.

Необходимость условий теоремы очевидна. В самом деле, связный граф порядка п не имеет изолированных вершин и число ребер в нем не менее п—1. Из леммы о рукопожатиях вытекает неравенство (1).

Достаточность докажем индукцией по длине после­довательности d. При п = 2 условиям теоремы удовлет­воряет только одна последовательность d=(1²). Реали­зацией этой последовательности служит связный граф К2, стало быть, для п = 2 теорема верна. Пусть теперь п > 2 и доказываемое утверждение верно для графиче­ских последовательностей, длины которых меньше п. От­дельно рассмотрим два случая: 1) d_n = 1, 2) d_n> 1.

1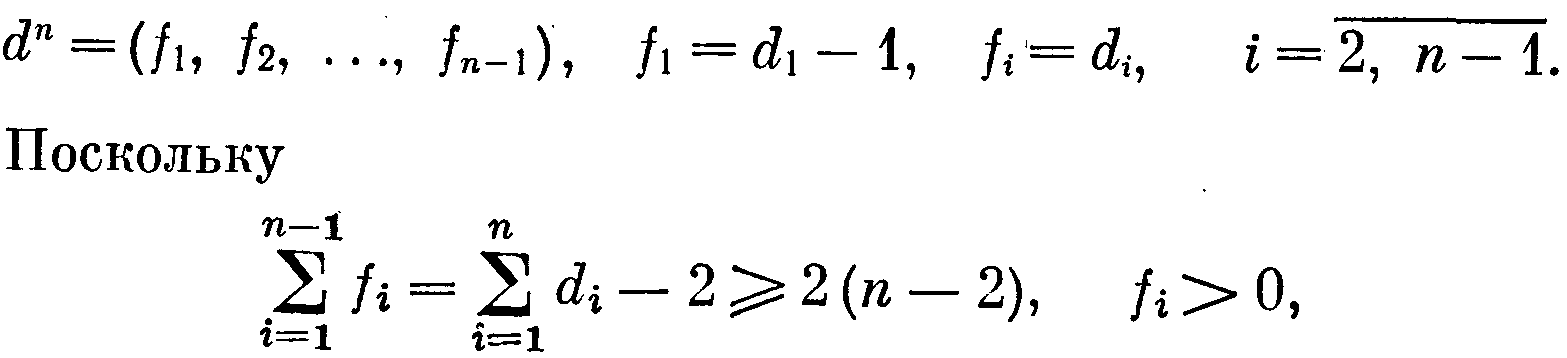)d_n = l. Так как n>2, то из неравенства (1) вы­текает, что d₁ > 1. Рассмотрим производную последова­тельность

то последовательность dⁿ удовлетворяет условиям тео­ремы.

2) d ⁿ>1. Снова будем различать две ситуации:

a) d_dn = 2 и б) d_dn>2.

В ситуации а) из условий теоремы следует, что

d_n = 2, d₂ = 2, d = (m, 2^n-1), m > 2.

Для производной последовательности dⁿ имеем

dⁿ=(f₁ ,f₂ , ...,f_n-1) = (m-1, 1,2^n-3),

В ситуации б) для производной последовательности dⁿ получаем

Итак, в любой ситуации производная последователь­ностьdⁿ удовлетворяет условиям теоремы и по индук­тивному предположению имеет связную реализацию Я, получаемую в результате описанной в формулировке тео­ремы l-процедуры. Добавив к графу Н новую вершину, смежную с вершинами степеней f₁ ,f₂ , ...,f_dn получим связную реализацию последовательности d.

Аналогично доказывается

Теорема 47.2.п-последователъностъ d может быть реализована деревом тогда и только тогда, когда она не содержит нулей и верно равенство

При выполнении указанных условий l-процедура постро­ит реализацию последовательности d деревом, если на каждом шаге выбирать в качестве ведущей вершину с минимальной положительной меткой.

. На рис. 47.1 показана Z-процедура, строящая дерево, которое является реализацией последовательности d = = (3², 2, 1⁴).

Перейдем к графам с более высоким числом реберной связности. Приведем без доказательства следующую тео­рему.

Теорема 47.3 (Д. Уэнг, 1976 г.). Каждая правиль­ная графическая п-последователъностъ d с d_n > 1 имеет ализацию, число реберной связности которой равно d_n .Такая реализация строится l-процедурощ на каждом шаге которой ведущей является вершина с минимальной положителъной меткой .

■+7

-•б

Счислом вершинной связности дело обстоит сложнее. Известно, что правильная графическая n-последовательность d может быть реализована графом с числом вершинной связности d_n или d_n — 1, причем соответствующую реализацию также можно получить посредством

L - процедуры. Однако доказательство этого факта и описание выбора ведущих вершин достаточно громоздки и потому здесь не приводятся.