34. Нормированная волновая функция, описывающая 1s-состояние электрона в атоме водорода, имеет вид , где a – первый боровский радиус. Определите среднее значение модуля кулоновской силы действующей на электрон.

35. Зная плотность льда ( = 917 кг/м³) и его температуру плавления (t_пл = 0 ^oC), оцените равновесное расстояние между молекулами воды и их энергию связи (в электрон-вольтах). Молярная масса воды – 1210^–3 кг/моль.

36. Используя статистический метод Томаса-Ферми, получите уравнение Томаса-Ферми для потенциала электрического поля многоэлектронного атома и запишите, в каком виде можно представить его решение.

------------------------------------------------------------------------------------------------------------------------

37. Частица массой m движется в одномерном потенциальном поле U(x) = kx²/2 (гармонический осциллятор). Волновая функция, описывающая поведение частицы в основном состоянии, имеет вид , где A – нормировочный коэффициент; a – положительная постоянная. Используя уравнение Шредингера, определите постоянную a.

38. Оцените энергию взаимного отталкивания атомов кремния (Z=14) в кристалле. Плотность кремния – 2.3310³ кг/м³, его молярная масса равна 2810^–3 кг/моль.

39. Считая внешнее электрическое поле квазиоднородным, выведите формулу для энергии взаимодействия диполя с этим полем. Анализируя полученную формулу, сделайте вывод о поведении жесткого диполя во внешнем квазиоднородном электрическом поле.

------------------------------------------------------------------------------------------------------------------------

40. Частица массой m движется в одномерном потенциальном поле U(x) = kx²/2 (гармонический осциллятор). Волновая функция, описывающая поведение частицы в основном состоянии, имеет вид , где A – нормировочный коэффициент; a – положительная постоянная. Используя уравнение Шредингера, определите энергию частицы в этом состоянии.

41. Зная плотность меди ( = 8930 кг/м³) и ее температуру плавления (t_пл = 1083 ^oC), оцените равновесное расстояние между атомами меди и их энергию связи (в электрон-вольтах). Молярная масса меди равна 6410^–3 кг/моль.

42. Зная, что на частицу, обладающую магнитным моментом , во внешнем квазиоднородном магнитном поле с индукцией действует момент сил 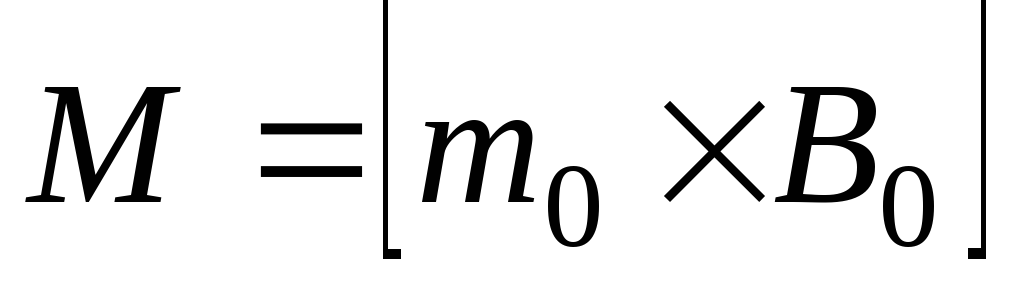, выведите формулу для энергии взаимодействия частицы с полем . Анализируя полученную формулу, сделайте вывод о поведении частицы во внешнем квазиоднородном магнитном поле.

------------------------------------------------------------------------------------------------------------------------

43. Определите (по теории Бора) изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона с длиной волны, равной 1,0210^–7 м.

44. Как показывают измерения, молекулы NO имеют магнитный момент, равный 1,8_B. Оцените, какую часть от полной энергии притяжения этих молекул составляет энергия магнитного взаимодействия. Относительная электроотрицательность азота равна 3,0, кислорода – 3,5; _B = 9,2710^–24 Дж/Тл.

45. Используя статистический метод Томаса-Ферми, получите уравнение Томаса-Ферми для потенциала электрического поля многоэлектронного атома и запишите, в каком виде можно представить его решение.

------------------------------------------------------------------------------------------------------------------------

46. Электрон в атоме находится в f-состоянии. Определите возможные значения (в единицах ) проекции момента импульса L_z орбитального движения электрона в атоме на направление внешнего магнитного поля.

47. Оцените дипольный момент и энергию взаимного притяжения молекул воды при нормальных условиях. Плотность воды – 10³ кг/м³, ее молярная масса равна 1810^–3 кг/моль.

48. Используя представления о дисперсионном взаимодействии атомов как взаимодействии двух мгновенных диполей, выведите формулу для энергии дисперсионного взаимодействия двух атомов водорода.

------------------------------------------------------------------------------------------------------------------------

49. Электрон в атоме находится в f-состоянии. Определите возможные значения проекции магнитного момента, обусловленного орбитальным движением этого электрона, на направление внешнего магнитного поля. Значение магнетона Бора _B = 9,2710^–24 Дж/Тл.

    Вычислите дипольный момент и тензор квадрупольного момента системы зарядов, изображенной на рисунке.

50. Используя разложение электрического поля системы зарядов по мультиполям, выведите формулу для потенциала электрического поля диполя.

------------------------------------------------------------------------------------------------------------------------

52. Электрон в атоме находится в d-состоянии. Определите 1) момент импульса (орбитальный) L электрона; 2) максимальное значение проекции момента импульса L_{z max} на направление внешнего магнитного поля.

53. Оцените дипольный момент и энергию взаимного притяжения молекул насыщенного водяного пара при нормальных условиях, если его давление составляет 2.34 кПа.

Используя планетарную модель атома Резерфорда-Бора (см. рис.), найдите поляризуемость атома водорода и оцените энергию дисперсионного взаимодействия двух таких атомов (в электрон-вольтах), которые находятся на расстоянии R = 4a0.

-------------------------------------------------------------------------------------------------------------------------

55. Электрон в атоме находится в d-состоянии. Определите 1) магнитный момент атома, обусловленный орбитальным движением этого электрона; 2) максимальное значение проекции этого магнитного момента на направление внешнего магнитного поля. Значение магнетона Бора _B = 9,2710^–24 Дж/Тл.

56. Оцените дипольный момент молекулы HCl и энергию (в электрон-вольтах) взаимного притяжения молекул хлороводорода при температуре 273 К и давлении 2 кПа. Относительная электроотрицательность Cl равна 3,0, H – 2,1.

57. Используя представления о дисперсионном взаимодействии атомов как взаимодействии двух мгновенных диполей, выведите формулу для энергии дисперсионного взаимодействия двух атомов водорода.

------------------------------------------------------------------------------------------------------------------------

58. Определите, во сколько раз орбитальный момент импульса L электрона, находящегося в f-состоянии, больше, чем для электрона в p-состоянии.

59. Используя потенциал Ленарда-Джонса

,

оцените значения констант B и C, а также среднюю энергию взаимодействия атомов в кристалле аргона при температуре 4 К, если известно, что плотность аргона при этой температуре  = 1770 кг/м³, энергия ионизации атомов аргона I = 15,76 эВ, а их поляризуемость  = 210^–27 м³. Молярная масса аргона равна 40 г/моль.

60. Считая внешнее электрическое поле квазиоднородным, выведите формулу для энергии взаимодействия диполя с этим полем. Анализируя полученную формулу, сделайте вывод о поведении жесткого диполя во внешнем квазиоднородном электрическом поле.

-------------------------------------------------------------------------------------------------------------------------

61. Определите, во сколько раз магнитный момент атома, обусловленный орбитальным движением электрона, находящегося в f-состоянии, больше магнитного момента атома, обусловленного орбитальным движением электрона в p-состоянии.

62. Оцените расстояние наибольшего сближения ионов фосфора (Z₁=15), имеющих энергию 100 кэВ, с атомами кремния (Z₂=14), которые практически неподвижно закреплены в кристаллической решетке кремния.

Используя планетарную модель атома Резерфорда-Бора (см. рис.), найдите поляризуемость атома водорода и оцените энергию дисперсионного взаимодействия двух таких атомов (в электрон-вольтах), которые находятся на расстоянии R = 4a0.

-------------------------------------------------------------------------------------------------------------------------

64. 1s электрон атома водорода, поглотив фотон с энергией 12,1 эВ, перешел в возбужденное состояние с максимально возможным орбитальным квантовым числом. Определите изменение момента импульса орбитального движения электрона.

65. Используя метод молекулярных орбиталей, постройте схему заполнения энергетических уровней электронами в молекуле N₂. Определите кратность химической связи в этой молекуле и суммарный спин электронов в ней. Сколько - и сколько -связей содержится в этой молекуле?

66. Зная, что на частицу, обладающую магнитным моментом , во внешнем квазиоднородном магнитном поле с индукцией действует момент сил , выведите формулу для энергии взаимодействия частицы с полем . Анализируя полученную формулу, сделайте вывод о поведении частицы во внешнем квазиоднородном магнитном поле.

-------------------------------------------------------------------------------------------------------------------------