Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

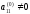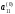первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки наи исключим x₁из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент приx₁в соответствующей строке. Получим

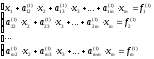
Если 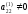то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

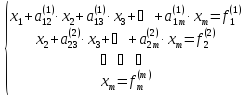
Из нее в обратном порядке находим все значения x_i:

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных –обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

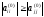, j = i+1,i+ 2, …, m;

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Метод простой итерации

При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами. Изложим здесь один из этих методов — метод итерации.

Пусть дана линейная система

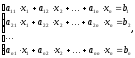
Введя в рассмотрение матрицы

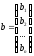
систему (1) коротко можно записать в виде матричного уравнения

Ах = b. (1')

Предполагая, что диагональные коэффициенты

a_ij ≠ 0 (i=1, 2,…., n),

разрешим первое уравнение системы (1) относительно x₁ , второе — относительно х₂ и т.д. Тогда получим эквивалентную систему

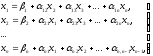
где

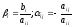при

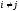
и 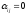приi=j (i,j=1,2,….,n).

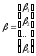
Введя матрицы

и .

систему (2) можем записать в матричной форме

x = β + ax

(2')

Систему (2) будем решать методом последовательных приближений. За нулевое приближение принимаем, например, столбец свободных членов

х⁽⁰⁾ = β

Далее, последовательно строим матрицы-столбцы

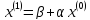
(первое приближение),

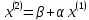
(второе приближение) и т.д

Вообще говоря, любое (k+1)-е приближение вычисляют по формуле

x(k+1) = β + ax(k)

(k= 0, 1, 2, ...)

(3)

Если последовательность приближений x⁽⁰⁾ , x⁽¹⁾ ,….,x^(k) ,…. имеет предел,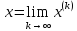

то этот предел является решением системы (2). В самом деле, переходя к пределу в равенстве (3), будем иметь:

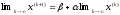
или

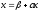
т. е. предельный вектор х является решением системы (2'), а, следовательно, и системы (1).

Напишем формулы приближений в развернутом виде:

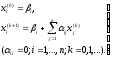
Заметим, что иногда выгоднее приводить систему (1) к виду (2) так, чтобы коэффициенты а_ij не были равны нулю. Например, уравнение

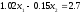
для применения метода последовательных приближений естественно записать в виде

x₁ = 2,7 — 0,02x₁ + 0,15x₂.

Вообще, имея систему

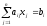(k = 1, 2, ... , n),

можно положить:

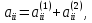
где 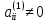. Тогда данная система эквивалентна приведенной системе

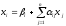(i=1,2,…,n).

где

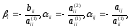при

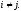
Поэтому при дальнейших рассуждениях мы не будем, вообще говоря, предполагать, что .

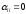Метод последовательных приближений, определяемых формулой (3) или (3'), носит название метода итерации. Процесс итерации (3) хорошо сходится, т. е. число приближений, необходимых для получения корней системы (1) с заданной точностью, невелико, если элементы матрицы а малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).