
- •Студенты
- •1. Содержание
- •2. Постановка задачи
- •3. Методы решения систем линейных алгебраических уравнений
- •Метод Гаусса
- •3.1.1 Условия применимости метода Гаусса
- •3.1.2 Обоснование и вывод формул
- •Теоремы с доказательствами Теорема об lu-разложении
- •Следствие
- •Элементарные треугольные матрицы
- •3.1.4 Алгоритм метода Гаусса
- •Метод простой итерации
- •3.2.1 Условия применимости метода простой итерации
- •3.2.3 Алгоритм метода простой итерации
- •Метод Зейделя
- •3.3.1 Обоснование и вывод формул
- •3.3.2 Условия применимости метода Зейделя
- •3.3.3 Приведение системы к виду, удобному для итераций
- •3.3.4 Алгоритм метода Зейделя
- •Метод Крамера
- •3.4.1 Условия применимости метода Крамера
- •Метод главных элементов
- •3.5.1 Условия применимости метода главных элементов.
- •3.5.2 Обоснование и вывод формул
- •Метод квадратных корней
- •3.6.1 Обоснование и вывод формул
- •3.6.2 Условие применимости метода квадратных корней
- •3.7.1 Условия применимости схемы Халецкого
- •3.7.2 Обоснование и вывод формул
- •Теория погрешностей
- •3.8.1 Источники и классификация погрешностей результата
- •3.8.2 Типы погрешностей
- •Проверка ручного счета средствами Excel
- •Метод Крамера
- •Метод простой итерации
- •Метод Зейделя
- •Метод Гаусса с выбором главного элемента
- •Метод квадратных корней
- •Язык Fortran
- •Метод Гаусса
- •Метод простых итераций
- •Метод Зейделя
- •Результаты и их анализ
- •Список использованной литературы
3.3.4 Алгоритм метода Зейделя
Проверяем условие сходимости метода.
|aij|
>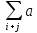 ij
ij
2. Приводим систему уравнений к нормальному виду: выражаемx1, x2, ….,xn.
3. Организуем итерационный процесс.

4. Задаем начальное приближение.
5. Проверяем точность найденного решения:
 ,где
,где задаваемая
точность, если она не задана, значит,
задаваемая
точность, если она не задана, значит, инженерная точность.
инженерная точность.
Метод Крамера
3.4.1 Условия применимости метода Крамера
Справедливо следующее утверждение (формулы Крамера).[1]c.268-269
Если определительD=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1, x2, ..., xn, определяемое формулами Крамера
xi=Di/ D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
Дана СЛАУ 5

Находим определитель СЛАУ. По формуле заменим i-ый столбец матрицы на столбец свободных членов

где i-номер строки,j-номер столбца
Аналогично находим определители для i=1,…,n.И по формуле найдём решения СЛАУ

Метод главных элементов
3.5.1 Условия применимости метода главных элементов.
Необходимое условие применения метода главных элементов: определитель системы не равен нулю.
3.5.2 Обоснование и вывод формул
Пусть дана линейная система[1]c.281-283

Рассмотрим расширенную прямоугольную матрицу, состоящую из коэффициентов системы и ее свободных членов,
M=
Выберем ненулевой, как правило, наибольший по модулю, не принадлежащий к столбцу свободных членов (q≠n+1) элемент apq матрицы М, который называется главным элементом, и вычислим множители
 ,
,
для всех i≠p.
Строка с номером р матрицы М, содержащая главный элемент, называется главной строкой. Далее, произведем следующую операцию: к каждой неглавной строке прибавим главную строку, умноженную на соответствующий множитель miдля этой строки. В результате мы получим новую матрицу, у которой q-й столбец состоит из нулей. Отбрасывая этот столбец и главную р-ю строку, получим новую матрицу с меньшим на единицу числом строк и столбцов. Над этой матрицей повторяем те же операции, после чего получаем новую матрицу и т. д. Таким образом, мы построим последовательность матриц, последняя из которых представляет двучленную матрицу-строку; ее также считаем главной строкой. Для определения неизвестных хг объединяем в систему все главные строки. После надлежащего изменения нумерации неизвестных получается система с треугольной матрицей, из которой легко шаг за шагом найти неизвестные данной системы.
Заметим, что метод Гаусса является частным случаем, метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. Запрограммировать метод главных элементов непросто, поэтому чтобы уменьшить вычислительную погрешность, применяют метод Гаусса с выбором главного элемента.
Метод квадратных корней
3.6.1 Обоснование и вывод формул
Пусть дана линейная система[1]c.283-284Ax=B,
где А = [аij] — симметрическая матрица, т.е.A' = [aji] =A. Тогда матрицу А можно представить в виде произведения двух транспонированных между собой треугольных матриц
A=T’T,
где
 и
и .
.
Производя перемножение матриц T’ и Т, для определения элементов tijматрицы Т получим следующие уравнения:

Отсюда последовательно находим

