
- •Студенты
- •1. Содержание
- •2. Постановка задачи
- •3. Методы решения систем линейных алгебраических уравнений
- •Метод Гаусса
- •3.1.1 Условия применимости метода Гаусса
- •3.1.2 Обоснование и вывод формул
- •Теоремы с доказательствами Теорема об lu-разложении
- •Следствие
- •Элементарные треугольные матрицы
- •3.1.4 Алгоритм метода Гаусса
- •Метод простой итерации
- •3.2.1 Условия применимости метода простой итерации
- •3.2.3 Алгоритм метода простой итерации
- •Метод Зейделя
- •3.3.1 Обоснование и вывод формул
- •3.3.2 Условия применимости метода Зейделя
- •3.3.3 Приведение системы к виду, удобному для итераций
- •3.3.4 Алгоритм метода Зейделя
- •Метод Крамера
- •3.4.1 Условия применимости метода Крамера
- •Метод главных элементов
- •3.5.1 Условия применимости метода главных элементов.
- •3.5.2 Обоснование и вывод формул
- •Метод квадратных корней
- •3.6.1 Обоснование и вывод формул
- •3.6.2 Условие применимости метода квадратных корней
- •3.7.1 Условия применимости схемы Халецкого
- •3.7.2 Обоснование и вывод формул
- •Теория погрешностей
- •3.8.1 Источники и классификация погрешностей результата
- •3.8.2 Типы погрешностей
- •Проверка ручного счета средствами Excel
- •Метод Крамера
- •Метод простой итерации
- •Метод Зейделя
- •Метод Гаусса с выбором главного элемента
- •Метод квадратных корней
- •Язык Fortran
- •Метод Гаусса
- •Метод простых итераций
- •Метод Зейделя
- •Результаты и их анализ
- •Список использованной литературы
Следствие
Метод Гаусса можно применять тогда и только тогда, когда все угловые миноры матрицы А отличны от нуля.
Элементарные треугольные матрицы
Мы уже видели, что метод Гаусса приводит к разложению исходной матрицы в произведение двух треугольных. Более детально описать структуру этих треугольных матриц можно с помощью так называемых элементарных треугольных матриц.[2]c.58-60
Матрица
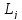 называется
элементарной нижней треугольной
матрицей, если она имеет вид
называется
элементарной нижней треугольной
матрицей, если она имеет вид
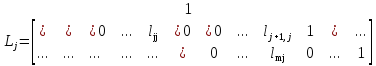
В матрице
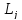 все
элементы главной диагонали кроме
все
элементы главной диагонали кроме равны
единице. Из остальных элементов отличными
от нуля могут быть только элементыj-го
столбца, расположенные ниже
равны
единице. Из остальных элементов отличными
от нуля могут быть только элементыj-го
столбца, расположенные ниже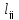 .
Обратной к
.
Обратной к является
элементарная нижняя треугольная матрица
является
элементарная нижняя треугольная матрица

Рассмотрим для наглядности сначала
систему
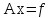 ,
состоящую из трех уравнений:
,
состоящую из трех уравнений:
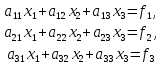 (15)
(15)
После первого шага исключения по методу Гаусса преобразованная система принимает вид
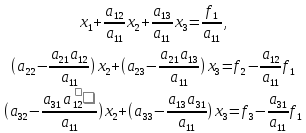 (16)
(16)
Отсюда видно, что матрица
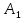 системы
(16) получается из исходной матрицы А
путем умножения А слева на элементарную
матрицу
системы
(16) получается из исходной матрицы А
путем умножения А слева на элементарную
матрицу
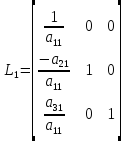 (17)
(17)
так что
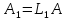 .
При этом систему (16) можно записать в
виде
.
При этом систему (16) можно записать в
виде
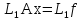
Матрицу (17) будем называть элементарной треугольной матрицей, соответствующей первому шагу исключения метода Гаусса. Перепишем систему (16) в виде
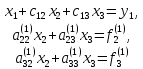 (18)
(18)
и осуществим второй шаг метода Гаусса,
т. е. исключим неизвестное
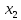 из
последнего уравнения. Тогда получим
систему вида
из
последнего уравнения. Тогда получим
систему вида
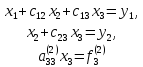 (19)
(19)
Нетрудно видеть, что переход от (18) к (19) осуществляется путем умножения системы (18) на элементарную треугольную матрицу
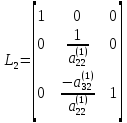 (20)
(20)
Таким образом, после второго шага исключения мы приходим к системе
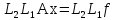 (21)
(21)
где матрицы
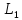 и
и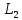 определены согласно (17), (20). Наконец,
умножая (21) на матрицу
определены согласно (17), (20). Наконец,
умножая (21) на матрицу
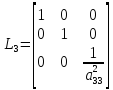
получаем систему
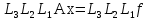 (22)
(22)
матрица, которой
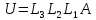 является
верхней треугольной матрицей с единичной
главной диагональю. Отсюда следует, в
частности, что A = LU, где
является
верхней треугольной матрицей с единичной
главной диагональю. Отсюда следует, в
частности, что A = LU, где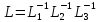 -
нижняя треугольная матрица. Таким
образом,LU-разложение
матрицы А может быть получено с помощью
элементарных треугольных матриц: сначала
строятся матрицы
-
нижняя треугольная матрица. Таким
образом,LU-разложение
матрицы А может быть получено с помощью
элементарных треугольных матриц: сначала
строятся матрицы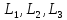 и
вычисляется
и
вычисляется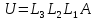 и
затем находится
и
затем находится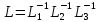 .
.
Отметим, что матрицы
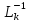 имеют
простой вид:
имеют
простой вид:
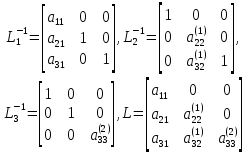
причем на диагонали матрицы L расположены ведущие элементы метода исключения.
Запись метода Гаусса в виде (22) детально описывает процесс исключения.
Все сказанное выше переносится без изменения и на системы уравнений произвольного порядка (2). Процесс исключения можно записать формулой
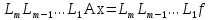 ,
(23)
,
(23)
где элементарная нижняя треугольная
матрица
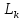 наk-м шаге исключения имеет
вид
наk-м шаге исключения имеет
вид

Матрица
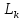 осуществляет
исключение неизвестного
осуществляет
исключение неизвестного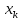 из
уравнений с номерами
из
уравнений с номерами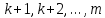 .
Матрицы
.
Матрицы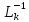 существуют
и имеют вид
существуют
и имеют вид

3.1.4 Алгоритм метода Гаусса
Пусть имеем систему m-линейных алгебраических уравнений
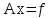 (1)
(1)
Запишем систему (1) в развёрнутом виде
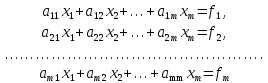 (2)
(2)
Необходимо решить систему (2) методом Гаусса.
Алгоритм решения.
1. Проверяем существование и единственность решения системы (2). Для этого находим ранг расширенной матрицы и матрицы коэффициентов.
2. Прямой ход метода Гаусса, то есть приводим систему (2) к треугольному виду так, чтобы на главной диагонали не было нулевых элементов.
Шаг 1.
Предположим,
что
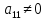 .
Поделив первое уравнение системы (2) на
.
Поделив первое уравнение системы (2) на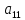 ,
получим
,
получим
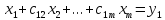 ,
(3)
,
(3)
где
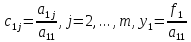
Рассмотрим теперь оставшиеся уравнения системы (2):
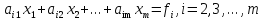 (4)
(4)
Умножим (3) на
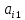 и
вычтем полученное уравнение изi-го
уравнения системы (4),
и
вычтем полученное уравнение изi-го
уравнения системы (4),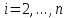 .
В результате получим следующую систему
уравнений:
.
В результате получим следующую систему
уравнений:
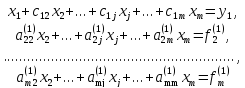 (5)
(5)
Здесь обозначено
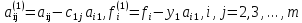 (6)
(6)
Матрица системы (5) имеет вид
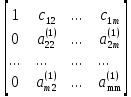
В системе (5) неизвестное
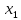 ,
содержится только в первом уравнении,
поэтому в дальнейшем достаточно иметь
дело с укороченной системой уравнений
,
содержится только в первом уравнении,
поэтому в дальнейшем достаточно иметь
дело с укороченной системой уравнений
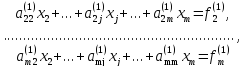 (7)
(7)
Тем самым мы исключили неизвестное
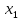 .
.
Шаг 2.
Если
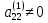 ,
то из системы (7) совершенно аналогично
можно исключить неизвестное
,
то из системы (7) совершенно аналогично
можно исключить неизвестное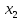 и
прийти к системе, эквивалентной (2), при
этом первое уравнение системы (5) остаётся
неизменным.
и
прийти к системе, эквивалентной (2), при
этом первое уравнение системы (5) остаётся
неизменным.
Шаг 3.
Исключая таким же образом неизвестные
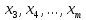 ,
придем окончательно к системе уравнений
вида
,
придем окончательно к системе уравнений
вида
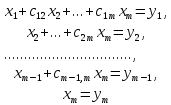 (8)
(8)
эквивалентной исходной системе (2).
Матрица этой системы
С= (9)
(9)
содержит нули всюду ниже главной диагонали. То есть мы привели систему к треугольному виду.
3. Обратный ход метод Гаусса заключается
в нахождении неизвестных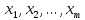
из системы (8). Поскольку матрица системы
имеет треугольный вид, можно
последовательно, начиная с
 ,
найти все неизвестные.
,
найти все неизвестные.
Действительно,
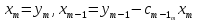 и
т. д. Общие формулы обратного хода имеют
вид
и
т. д. Общие формулы обратного хода имеют
вид
 (10)
(10)
4. И в заключение делаем проверку, то есть в систему (подставляем) найденное решение.
Простейший вариант метода Гаусса, называемый схемой единственного деления2, обладает следующим недостатком: если ведущий элемент akk какой-либо строки окажется равным нулю, то этот метод формально непригоден, хотя система может иметь единственное решение. Из этих соображений в схеме алгоритма добавлен поиск ненулевого ведущего элемента.
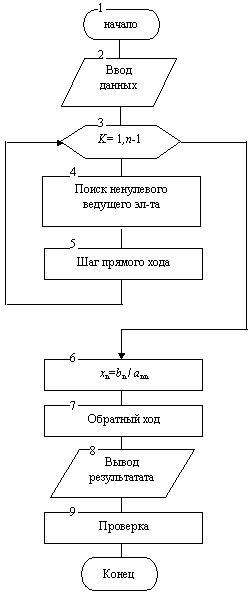
Рисунок 1.1 Схема алгоритма (блок-схема) метода Гаусса
На рисунках 1.2 - 1.6 представлены алгоритмы отдельных блоков метода.
Блок 2. С помощью двух вложенных циклов с управляющими переменными i=1,n и j=1,k организуем ввод коэффициентов ai,j и свободных членов bi исходной системы. Для того, чтобы в дальнейшем можно было выполнить в блоке 9 проверку результата, в алгоритме предусмотрено сохранение значений ai,j и bi исходной системы с помощью переприсвоений: cij=aij и di=bi
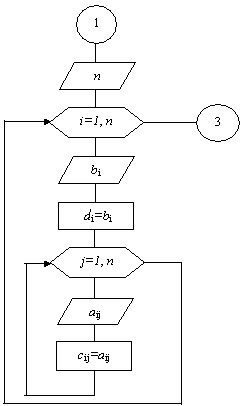
Рисунок 1.2 Ввод коэффициентов и свободных членов системы
Блок 3. Организуем цикл по k, внутри которого производится вычисление по всем шагам прямого хода. Последний п-й шаг прямого хода выводим из цикла.
Блок 4. На каждом шаге прямого хода выполняем поиск ненулевого ведущего элемента.
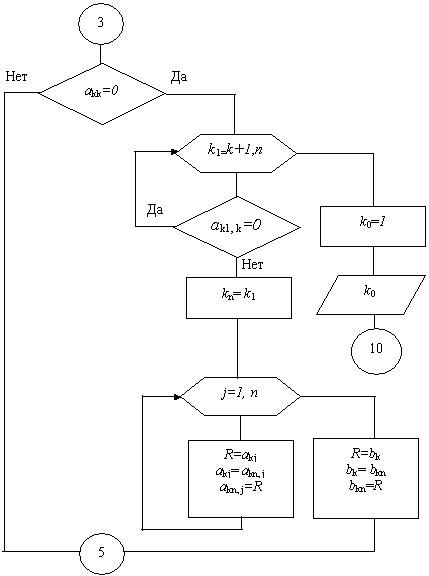
Рисунок 1.3 Поиск ненулевого ведущего элемента
Поиск ненулевого ведущего элемента ведётся в следующем порядке:
а) На каждом k-ом шаге прямого хода ведущий элемент каждой строки сравнивается с нулём;
б) Если в k-ой строке имеется нулевой ведущий элемент, то в k-ом столбце в цикле осуществляется поиск ненулевого элемента.
в) Если в какой-то строке kn такой ненулевой элемент найден, то строки kn и k поэлементно, в цикле по k1=(k+1), n , меняем местами. Для перестановки элементов используется рабочая переменная R.
г) Если ненулевой ведущий элемент не найден, то коду ошибки kо присваиваем значение 1 и расчёт прекращается.
Блок 5 - шаг прямого хода. На каждом шаге прямого хода проводим исключение неизвестных путём преобразования коэффициентов и свободных членов системы.
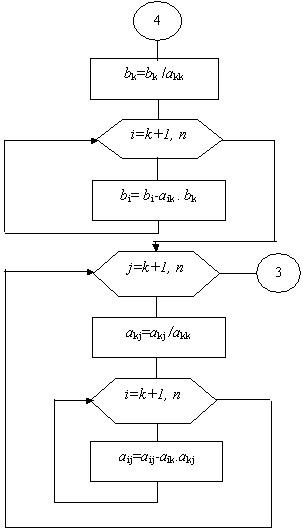
Рисунок 1.4 Шаг прямого хода
Блок 6. В этом блоке выведем из цикла по k последний шаг прямого хода, т.к. на этом шаге не нужны преобразования коэффициентов и свободных членов, а реализуется только одно вычисление
xn=bn/an,n
Блок 7 - обратный ход. В процессе обратного хода метода Гаусса из системы треугольного вида последовательно в обратном порядке в цикле по i=(n-1),1,-1 находим неизвестные системы по рекуррентной формуле
bi= bi - xj.ai,j , i=(n-1),1, j=(n+1),n.
При этом в цикле по j=(i+1),n использован приём последовательного вычитания xj.ai,j из bi,после чего вводится переприсвоение bi =хi.
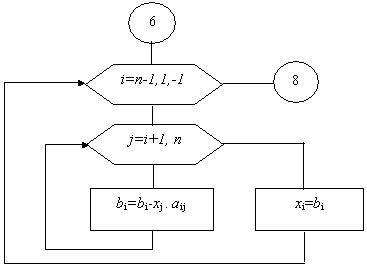
Рисунок 1.5 Шаг обратного хода
Блок 9 - проверка результата. В этом блоке подставляя значения полученных неизвестных в исходную систему и используя сохранённые значения коэффициентов системы ci,j и свободных членов di, проводим проверку решения задачи по формуле

Если корни системы найдены, то Fi – это число, близкое к нулю.
Блок 9 в алгоритме метода Гаусса рекомендуется использовать только в процессе отладки метода.
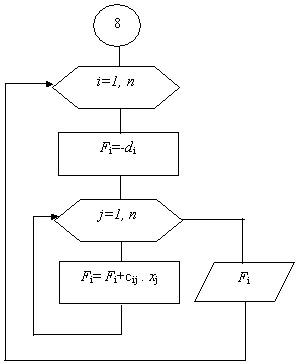
Рисунок 1.6 Проверка результата
-итерационные- методы, которые даже в отсутствии ошибок округления, дают лишь приближенное значение. К ним относятся методы Зейделя и простой итерации.
Описание методов:
