
- •Студенты
- •1. Содержание
- •2. Постановка задачи
- •3. Методы решения систем линейных алгебраических уравнений
- •Метод Гаусса
- •3.1.1 Условия применимости метода Гаусса
- •3.1.2 Обоснование и вывод формул
- •Теоремы с доказательствами Теорема об lu-разложении
- •Следствие
- •Элементарные треугольные матрицы
- •3.1.4 Алгоритм метода Гаусса
- •Метод простой итерации
- •3.2.1 Условия применимости метода простой итерации
- •3.2.3 Алгоритм метода простой итерации
- •Метод Зейделя
- •3.3.1 Обоснование и вывод формул
- •3.3.2 Условия применимости метода Зейделя
- •3.3.3 Приведение системы к виду, удобному для итераций
- •3.3.4 Алгоритм метода Зейделя
- •Метод Крамера
- •3.4.1 Условия применимости метода Крамера
- •Метод главных элементов
- •3.5.1 Условия применимости метода главных элементов.
- •3.5.2 Обоснование и вывод формул
- •Метод квадратных корней
- •3.6.1 Обоснование и вывод формул
- •3.6.2 Условие применимости метода квадратных корней
- •3.7.1 Условия применимости схемы Халецкого
- •3.7.2 Обоснование и вывод формул
- •Теория погрешностей
- •3.8.1 Источники и классификация погрешностей результата
- •3.8.2 Типы погрешностей
- •Проверка ручного счета средствами Excel
- •Метод Крамера
- •Метод простой итерации
- •Метод Зейделя
- •Метод Гаусса с выбором главного элемента
- •Метод квадратных корней
- •Язык Fortran
- •Метод Гаусса
- •Метод простых итераций
- •Метод Зейделя
- •Результаты и их анализ
- •Список использованной литературы
3.1.2 Обоснование и вывод формул
При реализации прямого хода метода
Гаусса нет необходимости действовать
с переменными
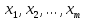 .
Достаточно указать алгоритм, согласно
которому исходная матрица А преобразуется
к треугольному виду и указать
соответствующее преобразование правых
частей системы. Получим эти общие
формулы.[2]c.54-55
.
Достаточно указать алгоритм, согласно
которому исходная матрица А преобразуется
к треугольному виду и указать
соответствующее преобразование правых
частей системы. Получим эти общие
формулы.[2]c.54-55
Пусть осуществлены первые k-1 шагов, т.
е. уже исключены переменные
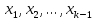 .
Тогда имеем систему
.
Тогда имеем систему
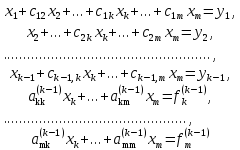 (1)
(1)
Рассмотрим k-e уравнение этой системы
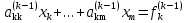
и предположим, что
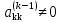 .
Поделив обе части этого уравнения на
.
Поделив обе части этого уравнения на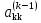 ,
получим
,
получим
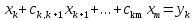 ,
(2)
,
(2)
где
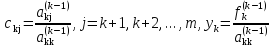
Далее, умножим уравнение (2) на
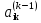 и
вычтем полученное соотношение из i-гo
уравнения системы (1), где
и
вычтем полученное соотношение из i-гo
уравнения системы (1), где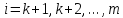 .
.
В результате последняя группа уравнений системы (1) примет вид:
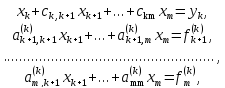
где
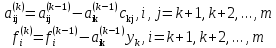
Таким образом, в прямом ходе метода Гаусса коэффициенты уравнений преобразуются по следующему правилу:
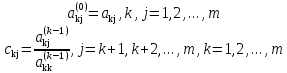 (3)
(3)
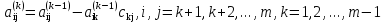 (4)
(4)
Вычисление правых частей системы осуществляется по формулам:
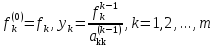 (5)
(5)
 (6)
(6)
Коэффициенты
 и
правые части
и
правые части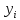 ,
,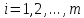 ,
,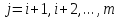 ,
хранятся в памяти компьютера и используются
при осуществлении обратного хода по
формулам.
,
хранятся в памяти компьютера и используются
при осуществлении обратного хода по
формулам.
Основным ограничением метода является
предположение о том, что все элементы
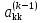 ,
на которые проводится деление, отличны
от нуля. Число
,
на которые проводится деление, отличны
от нуля. Число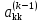 называется
ведущим элементом на k-м шаге исключения.
Даже если какой-то ведущий элемент не
равен нулю, а просто близок к нему, в
процессе вычислений может происходить
сильное накопление погрешностей. Выход
из этой ситуации состоит в том, что в
качестве ведущего элемента выбирается
не
называется
ведущим элементом на k-м шаге исключения.
Даже если какой-то ведущий элемент не
равен нулю, а просто близок к нему, в
процессе вычислений может происходить
сильное накопление погрешностей. Выход
из этой ситуации состоит в том, что в
качестве ведущего элемента выбирается
не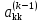 ,
а другое число (т. е. на k-м шаге исключается
не
,
а другое число (т. е. на k-м шаге исключается
не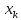 ,
а другое переменное
,
а другое переменное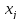 ,
,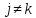 ).
Наиболее последовательно такая стратегия
выбора ведущих элементов осуществлена
в методе Гаусса с выбором главного
элемента.
).
Наиболее последовательно такая стратегия
выбора ведущих элементов осуществлена
в методе Гаусса с выбором главного
элемента.
Теоремы с доказательствами Теорема об lu-разложении
Пусть все угловые миноры матрицы А
отличны от нуля,
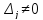 ,
,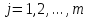 .
Тогда матрицу А можно представить,
причем единственным образом, в виде
произведения[2]c.55-57
.
Тогда матрицу А можно представить,
причем единственным образом, в виде
произведения[2]c.55-57
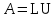 (8)
(8)
где L - нижняя треугольная матрица с ненулевыми диагональными элементами и U - верхняя треугольная матрица с единичной диагональю.
Доказательство.Докажем сформулированное утверждение сначала для матриц второго порядка. Будем искать разложение матрицы
A=
в виде
A=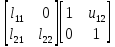 ,
,
где
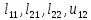 -
неизвестные пока числа. Для их нахождения
придем к системе уравнений
-
неизвестные пока числа. Для их нахождения
придем к системе уравнений
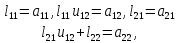
По предположению теоремы
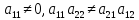 ,
следовательно, элементы
,
следовательно, элементы и
и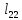 отличны
от нуля.
отличны
от нуля.
Дальнейшее доказательство проведем методом индукции. Пусть утверждение теоремы справедливо для матриц порядка k-1; докажем, что оно справедливо и для матриц порядка k. Представим матрицу А порядка k в виде
A=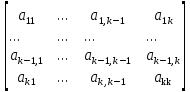 (9)
(9)
и обозначим

Согласно предположению индукции
существует требуемое разложение матрицы
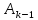 ,
т. е.
,
т. е.
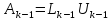 ,
,
где
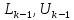 -
соответственно нижняя и верхняя
треугольные матрицы, обладающие
указанными в теореме свойствами. Будем
искать разложение матрицы (9) в виде
-
соответственно нижняя и верхняя
треугольные матрицы, обладающие
указанными в теореме свойствами. Будем
искать разложение матрицы (9) в виде
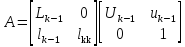 , (10)
, (10)
где
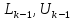 -
неизвестные пока векторы,
-
неизвестные пока векторы,
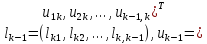
Перемножая матрицы в правой части уравнения (10) и учитывая (9), приходим к системе уравнений:
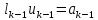 (11)
(11)
 (12)
(12)
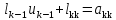 (13)
(13)
Из предположения индукции следует
существование матриц
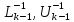 .
Поэтому из (11) и (12) получим
.
Поэтому из (11) и (12) получим
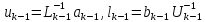
и, далее,
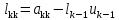
Таким образом, LU-разложение
матрицы А порядка k существует. Остается
доказать, что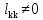 .
Рассмотрим определитель матрицы А. Из
разложения (10) следует, что
.
Рассмотрим определитель матрицы А. Из
разложения (10) следует, что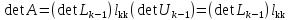 .
По условию теоремы
.
По условию теоремы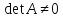 ,
следовательно,
,
следовательно,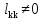 .
Тем самым индукция завершена и доказана
возможность требуемого разложения.
Покажем теперь, что такое разложение
единственно. Предположим, что матрицу
А можно разложить двумя способами:
.
Тем самым индукция завершена и доказана
возможность требуемого разложения.
Покажем теперь, что такое разложение
единственно. Предположим, что матрицу
А можно разложить двумя способами:
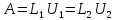
Тогда
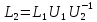 и
и
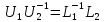 (14)
(14)
Матрица в левой части уравнения (14)
является верхней треугольной, а в правой
части - нижней треугольной. Такое
равенство возможно лишь в случае, если
матрицы
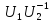 и
и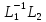 диагональные.
Но на диагонали матрицы
диагональные.
Но на диагонали матрицы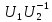 (а
следовательно, и матрицы
(а
следовательно, и матрицы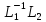 )
стоят единицы, следовательно, эти матрицы
единичные:
)
стоят единицы, следовательно, эти матрицы
единичные:
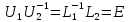
Отсюда получаем
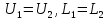 ,
т. е. разложение (8) единственно.
,
т. е. разложение (8) единственно.
Теорема об LU- разложении полностью доказана.
