Язык Fortran
Метод Гаусса
Таблица идентификаторов
В таблице 8 приведены основные идентификаторы, используемые в программе, реализующей метод Гаусса на языке Fortran.
Таблица 8 – Идентификаторы для метода Гаусса
|
Название переменной |
Тип |
Описание |
|
N |
int |
Размерность матрицы коэффициентов |
|
matrix [N][ N+1] |
double |
Матрица коэффициентов + свободные члены |
|
x [N] |
double |
Корни |
//gaus.for
|
1 |
2-5 |
6 |
9 72 |
|
|
|
|
program gauss real temp, e integer i, j, k, N real, allocatable :: matrix(:,:), x(:) print*, " Enter the the number of x =" read*, N allocate (matrix(N,N)) allocate (x(N)) print*, " Enter the coefficients " do i=1, N do j=1, N+1 print*, "A[",i,"][",j,"]" read*, matrix(i,j) enddo enddo do i=1,N if(matrix(i,i)==0) then print*,'input error (matrix(i,i)=0)' stop endif enddo do i = 1,N write(*,*) (matrix(i,j), j=1,N+1) end do !прямой ход do i = 1,N do j = i+1,N temp = (matrix(j,i))/(matrix(i,i)) do k = 1,N+1 matrix(j,k)=matrix(j,k)-matrix(i,k)*temp end do end do end do !обратный ход x(N) = matrix(N,N+1)/matrix(N,N) do i = N-1,1,-1 temp = 0.0 do j = i+1, N temp = temp + matrix(i,j)*x(j) end do temp = matrix(i,N+1) - temp x(i) = temp/matrix(i,i) end do !ответ do i=1, n print*,"x(",i,")=",x(i) enddo end program
|
На рисунках 2.14 и 2.15 приведены примеры работы программы, реализующей метод Гаусса на языке Fortran. Программа последовательно предлагает ввести коэффициенты, после чего выводит результат на экран.
Пример работы программы:
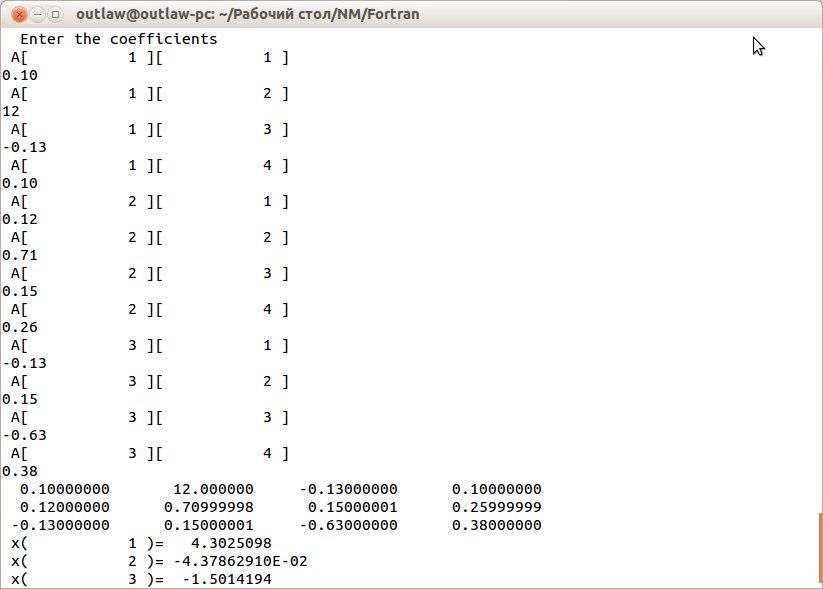
Рисунок 2.14 – окно с результатом работы программы, реализующей метод Гаусса на языке Fortran (Король)
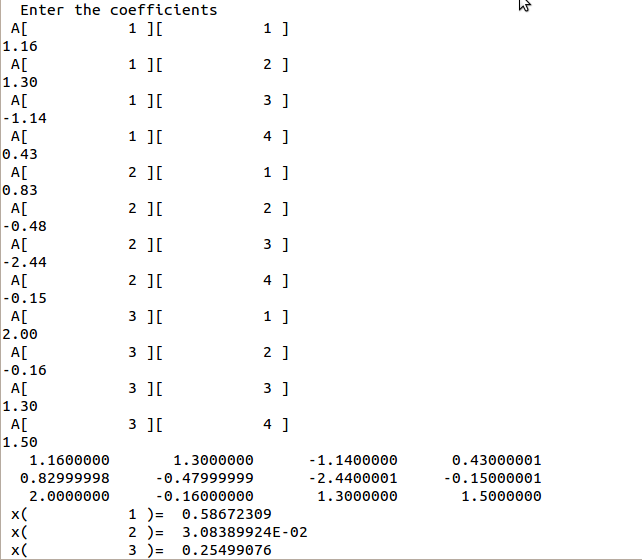
Рисунок 2.15 – окно с результатом работы программы, реализующей метод Гаусса на языке Fortran (Скворцова)
Метод простых итераций
Таблица идентификаторов
В таблице 9 приведены основные идентификаторы, используемые в программе, реализующей метод простых итераций на языке Fortran.
Таблица 9 – Идентификаторы для метода простых итераций
|
Название переменной |
Тип |
Описание |
|
N |
int |
Размерность матрицы коэффициентов |
|
matrix[N][N+1] |
double |
Матрица коэффициентов + свободные члены |
|
x_old [N] |
double |
Корни подсчитанные на i-ой итерации |
|
x [N] |
double |
Корни |
|
exp |
double |
Погрешность вычисления |
//iter.for
|
1 |
2-5 |
6 |
9 72 |
|
|
|
|
program iter implicit none character*64 file_name real matrix(100,101), x(100), x_old(100), summa, eps integer i, j, k, N write(*,*) "Enter file name: " read(*, *)file_name !чтение матрицы из файла open(3, FILE = file_name) read(3,*) N !размерность матрицы do i = 1,N read(3,*) (matrix(i,j), j=1,N+1) end do !печать матрицы do i = 1,N write(*,*) (matrix(i,j), j=1,N+1) x(i) = 0.0 x_old(i) = 1.0 end do write(*,*) "Entereps: " read(*,*)eps
!проверка на сходимость do i = 1,N summa=0.0 do j = 1,N summa = summa + abs(matrix(i,j)) end do summa = summa - abs(matrix(i,i)); if (summa > abs(matrix(i,i))) then stop ' diverges' end if end do
!делать итерации, пока не будет достигнута точность do while(.true.) do i = 1,N ! проверка, не достигнута ли заданная точность if(abs(x(i) - x_old(i)) < eps) then do k=1, N print*,"x(",k,")=",x(k) enddo stop end if end do do i = 1,N x_old(i) = x(i) end do do i = 1,N summa = 0.0; do j = 1,N if (i /= j) then summa = summa + (x_old(j)*matrix(i,j)); end if end do x(i) = (matrix(i,N+1)-summa)/matrix(i,i); end do end do end program
|