30. Система случайных величин, закон распределения вероятностей дискретной двумерной случайной величины.
Дискретная случайная величина (ДСК) – величина, принимающая счетное (конечное или бесконечное) множество значений.
Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, ..., n числами. Такие величины называются соответственно двумерными, трехмерными, . . ., n-мерными.
Двумерную случайную величину обозначают (X, Y). Каждую из величин X и Y называют составляющей; обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично n-мерную величину можно рассматривать как систему n случайных величин.
Законом
распределения дискретной двумерной
случайной
величины называют перечень возможных
значений этой величины, т. е. пар чисел 
и
их вероятностей p
. Обычно
закон
распределения задают в виде таблицы.
Первая
строка таблицы содержит все возможные
значения
составляющей Y, а
первый столбец — все возможные значения
составляющей X. В
клетке, стоящей на пересечении i-ой
строки и j-го
столбца указана вероятность того,
что случайная величина примет значение 
:
Зная
закон распределения двумерной дискретной
случайной
величины, можно найти законы
распределения каждой
из составляющих: вероятность
того, что X примет
значение 
равна
сумме вероятностей «строки 
». Аналогично
и для других значений x.
Т.е. имеем
и
т.д.
Аналогично сложив
вероятности «столбца 
»,
получим вероятность того, что случайная
величина
Замечание. Сумма вероятностей всех клеток таблицы закона распределения равна 1, т.е.
.
31. Функция распределения двумерной случайной величины, ее свойства.
Рассмотрим двумерную случайную величину (X, Y) (безразлично, дискретную или непрерывную).
Пусть х, у - пара действительных чисел. Вероятность события, состоящего в том, что случайная величина X примет значение, меньшее х, и при этом случайная величина Y примет значение, меньшее у, обозначим через F(x, у). Если х и у будут изменяться, то будет изменяться и F(х, у), т. е. F (х, у) есть функция от х и у.
Функцией распределения двумерной случайной величины (X, Y) называют функцию F (х, у), определяющую для каждой пары чисел х, у вероятность того, что X примет значение, меньшее х, и при этом Y примет значение, меньшее у:
(9.1)
Геометрически это равенство можно истолковать так: F (х, у) есть вероятность того, что случайная точка (X, Y) попадет в бесконечный квадрант расположенный левее и ниже вершины, которая имеет координаты (x, у):
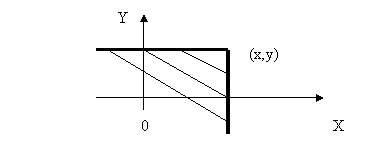
Свойства функции распределения двумерной случайной величины
1. Значения функции распределения удовлетворяют неравенству:
2. F(x,y) есть неубывающая функция по каждому аргументы, т.е.:
если 
и
3. Имеют место предельные соотношения:
4. При 
функция
распределения двумерной случайной
величины становится функцией распределения
составляющейX:
При 
функция
распределения двумерной случайной
величины становится функцией распределения
составляющейY:
Плотность совместного распределения вероятностей непрерывной случайной величины, нахождение функции распределения системы по известной плотности распределения.
Двумерная случайная величина задается функцией распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения.
Плотностью совместного распределения вероятностей f (x, у) двумерной непрерывной случайной величины (X, У) называют вторую смешанную частную производную от функции распределения:
Зная плотность совместного распределения f (x, у), можно найти функцию распределенияF (x, у) по формуле
Свойства двумерной плотности вероятности, отыскание плотностей составляющих двумерной случайной величины.
1. Двумерная плотность вероятности неотрицательна:
2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
(9.9)
Это свойство часто называют условием нормировки вероятностей. Свойство позволяет находить параметры плотности вероятности.