56.Проверка гипотезы о законе распределения. Хи-квадрат критерий Пирсона.

При объеме выборки  для проверки гипотезы о законе распределения используют критерий c² (критерий Пирсона, критерий согласия). Он применяется для группированных данных (как при построении гистограммы), когда в каждом интервале находится не менее 5 измерений (иначе интервал называется малонаселенным). Если число измерений в интервале оказывается меньше 5, тогда он объединяется с соседним. Если рассматривать частоту i-го интервала как случайную величину, то – число появлений «успеха» внезависимых испытаниях, где под «успехом» понимается попадание случайной величиныв-й интервал. Таким образом, вероятность «успеха» равна, а случайная величинаимеет биномиальное распределение с параметрамии. В частности,. Рассмотрим статистику c² – функцию от случайных величин , определяемую формулой

,

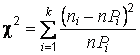где – число данных вi-м интервале (),– теоретическая вероятность попадания случайной величинывi-й интервал, – объем выборки,– число интервалов.

Можно показать, что, если закон распределения генеральной совокупности подобран правильно, то с ростомслучайную величинуможно считать распределенной по распределениюс числом степеней свободы;– числом параметров проверяемого закона распределения,вычисленных по выборке. Следует обратить внимание на то, что число степеней свободы – это число независимых слагаемых в сумме 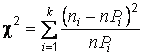, т. е. общее число слагаемых минус число наложенных уравнений связи. В общем случае по выборке оцениваютпараметров.

57.Проверка гипотезы о законе распределения. Критерий Колмогорова.

По результатам выборки объёмом nстроится эмпирическая функция распределенияF(х). Принимается гипотеза Н₀: случайная величина Х подчиняется распределению описанному функциейF(x).

За меру расхождения функций принимается величина:

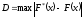
Существуют таблицы распределения Колмогорова в которых можно найти:

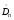- критическое значение. Оно зависит от уровня значимости α(Р = 1 - α), величиныDи величины выборкиn.

Если полученные из опыта значения коэффициента Dоказывается больше критического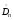, то Н₀отвергается.

Если

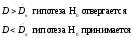
С помощью величины 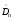можно построить доверительные границы для неизвестной функцииF(x):

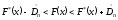
Колмогоров показал, что при n→ ∞ величина:

подчиняется распределению Колмогорова.

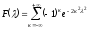
Критерий Колмогорова так же может быть использован для статистической проверки принадлежности двух выборок объёмом n₁иn₂к одной и той же генеральной совокупности. Вычисляется параметр λ:

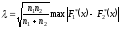
где: 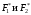- эмпирические функции распределения соответственно первой и второй выборки.

По величине λ судят о согласии.

58.Проверка гипотезы о законе распределения. Критерий Колмогорова-Смирнова.

- непараметрический критерий, применяемый для проверки гипотезы Н ₀, согласно к-рой независимые случайные величины Х ₁, ..., Х _п имеют заданную непрерывную функцию распределения F(x)против односторонней альтернативы : где - математическое ожидание функции эмпирического распределения F_n(x). К.- С. к. построен на статистике

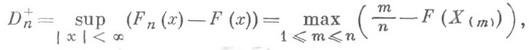
где - вариационный ряд, полученный по выборке Х _х, ..., Х _п.Таким образом, К.- С. к. является вариантом Колмогорова критерия для проверки гипотезы Н₀ против односторонней альтернативы Изучая распределение статистики D⁺_n, Н. В. Смирнов [1] показал, что

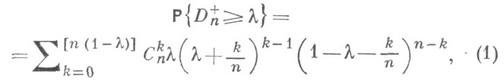
где 0<Х<1, [а] - целая часть числа а. Кроме точного распределения (1) статистики Н. В. Смирнов получил также ее предельное распределение, именно: если и 0<l₀<=О( п^1/6), то

где l₀- любое положительное число. С помощью техники асимптотических пирсоновских преобразований было показано [2], что если и 0<l₀<l=О(), то

Согласно К.- С. к. с уровнем значимости aгипотезу H₀ следует отвергнуть, коль скоро

причем, в силу (2),.

Аналогично поступают при проверке гипотезы Н ₀ против альтернативы :

В этом случае статистикой К.- С. к. является случайная величина

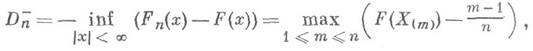
распределение к-рой, при справедливости гипотезы Н ₀, совпадает с распределением статистики