
- •Классическое определение вероятности.
- •Формула сложения вероятностей.
- •Формула полной вероятности.
- •Повторные независимые испытания
- •Формула Бернулли
- •1.10. Теоремы Муавра-Лапласа
- •13.Случайные величины: дискретные и непрерывные случайные дискретные величины
- •Пуассона распределение
- •Свойства
- •Свойства
- •Гипергеометрическое распределение.
- •1. Дискретная случайная величина, закон и функция распределения
- •2. Числовые характеристики дискретных случайных величин
- •30. Система случайных величин, закон распределения вероятностей дискретной двумерной случайной величины.
- •31. Функция распределения двумерной случайной величины, ее свойства.
- •Свойства функции распределения двумерной случайной величины
- •Определение плотностей вероятности составляющих двумерной случайной величины:
- •Понятие ковариация и коэффициента корреляции
- •41. Линейная регрессия. Линейная корреляция. Нормальная корреляция
- •42.Закон больших чисел. Лемма Чебышева.
- •43.Неравенство Чебышева.
- •44.Теорема Чебышева.
- •45.Теорема Бернули.
- •46. Центральная предельная теорема.
- •47. Основные понятия математической статистики: вариационный ряд, его характеристики.
- •48. Средние величины, показатели вариации.
- •50. Понятие оценки параметров.
- •51. Методы нахождения оценок: метод моментов, метод максимального правдоподобия, метод наименьших квадратов.
- •52. Понятие статической гипотезы и схеме ее проверки.
- •56.Проверка гипотезы о законе распределения. Хи-квадрат критерий Пирсона.
- •57.Проверка гипотезы о законе распределения. Критерий Колмогорова.
- •58.Проверка гипотезы о законе распределения. Критерий Колмогорова-Смирнова.
51. Методы нахождения оценок: метод моментов, метод максимального правдоподобия, метод наименьших квадратов.
Метод наибольшего (максимального) правдоподобия (МНП)(ММП) обладает следующими достоинствами:
1. Всегда приводит к состоятельным оценкам (иногда смещенным)
2. Получаемые оценки распределены асимптотически нормально и имеют минимально возможную дисперсию по сравнению с другими асимптотически нормальными оценками.
Недостаток: требуется решать громоздкие системы уравнений.
Имеется СВ Х, f(x,q) – функция ее плотности вероятности, выражение которой известно.
q– неизвестный параметр, подлежащий оценке.
x1,x2,…,xn–nнезависимых наблюдений над СВx.
В основе МНП лежит функция L(q) – функция правдоподобия, формирующаяся с учетом свойств многомерной функции распределения наблюдений над СВ х.
f(x1, x2,…,xn,q)=f(x1, q)×f(x2,q)×…×f(xn,q)
В указанное равенство подставляются данные и получаем функцию L(q):
L(q)=f(x1,q)×f(x2,q)×…×f(xn,q)
За
максимальное правдоподобное значение
параметра qпринимаем ,
при которойL(q)
максимально.
,
при которойL(q)
максимально.
Метод моментов(Метод Пирсона).
Метод обладает следующими достоинствами:
Оценки получаемые этим методом всегда являются состоятельными.
Метод моментов мало зависит от закона распределения случайной величины.
Сложность вычисления незначительна.
Известна случайная величина Х, которая характеризуется f(x,θ1,θ2…θq), аналитический вид этой функции известен.
По выборке объёмом nх1,х2,х3,…хn– значения случайной величины в выборке вычисляем эмпирические начальные моменты случайной величины:
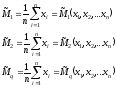
Находим теоретические моменты:

Основная идея метода моментов заключается в приравнивании значения эмпирических значений моментов теоретическим.
Метод наименьших квадратов.
Параметры уравнения регрессии определяются методом наименьших квадратов, предложенным Лагранжем и Гауссом, который сводится к следующему.
Строятся квадратичные формы:

xi– измеренное значение переменной,
e- истинное или теоретическое значение этой величины.
Требуется, чтобы сумма квадратов отклонений измеренных значений относительно истинных была минимальна.
52. Понятие статической гипотезы и схеме ее проверки.
Типы и общая схема проверки статистических гипотез
Типы статистических гипотез определяются совокупностью тех задач и методов их решения, которые имеют место в психолого-педагогических исследованиях. По своим прикладным содержанием статистические гипотезы можно разделить на несколько основных х типов по:
o закона распределения случайных величин тех или иных свойств;
o численных показателей параметров (средних, дисперсий, корреляций и др.);
o однородности двух или нескольких выборок
o различий в уровне признаков изучаемого явления или процесса;
o различий в распределении признаков
Общая схема проверки статистических гипотез Несмотря на разнообразие типов гипотез и критериев, схему проверки статистических гипотез можно представить в виде последовательности следующих процедур:
1) формулировка гипотез Н0 и Ні на основе задач исследования;
2) проверка предположений относительно соответствия распределения параметрическом семейству, параметров выборки и другой дополнительной информации;
3) принятие уровня значимости а;
4) выбор статистического критерия;
5) расчеты эмпирического критерия;
6) определение области критических значений критерия;
7) принятие статистического решения;
8) формулировка статистических выводов;
9) принятие решения о продлении (прекращении) исследований;
10) формулировка содержательных выводов.
53.
54.
55.
