Пример курсача МСС 2

Задание:

1. Определить главные деформации и их направления;

2. Определить модуль и интенсивность деформации;

3. Определить деформации на октаэдрической площадке;

4. Определить экстремальные деформации сдвига, площадки сдвига, на которых они действуют, а также деформацию растяжения – сжатия на этих площадках;

5. Определить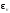идля направления (,)через

6. Показать на диаграмме деформаций Мора:,,,

7. По заданному тензору Коши и главным линейным деформациям определить тензор напряжений для упругого изотропного тела прииМПа. Показать на гранях куба эти напряжения;

8. Определить по условиюв какой области деформирования (упругой или упруго-пластичной) находится материал при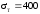МПа;

Дано:

1. Определение главных величин деформации и положение главных осей деформаций

1. Определим среднюю линейную деформацию :

2. Определим девиатор деформаций:

– девиатор напряжений, где и ;

В результате получаем:

3. Записываем кубическое уравнение:

где

В итоге получаем:

(1)

4. Определение корней уравнения (1): , , 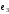с помощью итерационного метода:

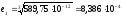
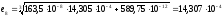
Точность:

Обозначим

Запишем условие инвариантности:

где известно.

Составляем квадратное уравнение:

Таккак, получаем:

Проверка:

5. Определим главные линейные деформации.

6. для определения главных осей деформаций запишем следующую систему уравнений:

Определим, , :

;

При

_{Получаем:}

Проверка:

При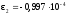

Получаем:

Проверка:

При

Получаем:

Проверка:

7. Проверка условий ортогональности:

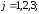
Рисунок 1

2. Определения модуля и интенсивности деформации

1. Определение модуля тензора деформации:

- модуль тензора деформации

где

2. Определение интенсивности тензора деформации:

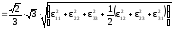
Модуль и интенсивность деформации взаимосвязаны следующим отношением:

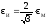где

3. Определение деформации по октаэдрической площадке

-октаэдрическая угловая деформация

- интенсивность тензора деформации

Из сравнения и находим, что 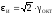, следовательно

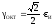, где

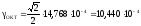
- объемная относительная деформация

4. Определение экстремальных деформаций сдвига и площадок, на которых они действуют (а также линейных деформаций на этих площадках)

, - экстремальные деформации чистого сдвига

, - линейные деформации на площадках экстремального сдвига

(Рисунок 2)

(Рисунок 3)

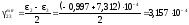
(Рисунок 4)

Рисунок 2

Рисунок 3

Рисунок 4

5. Определениеи при заданном направлении

r(,)

1. Определение линейной деформации

- угловая деформация междуи

Построение диаграммы Мора

7. Определениетензоранапряжений (при и МПа)

1. Находим девиатор напряжений

где ,

, МПа

ГдеЕ– модуль Юнга, – коэффициент Пуассона, – модуль сдвига

-девиатор деформации

В итоге имеем: МПа

Находим тензор напряжений Эйлера

где ,

- среднее напряжение, где

, МПа

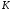– модуль объемной упругости

Мпа

В итоге имеем: МПа

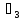
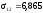
Рисунок 6

2. Находим главные напряжения

где МПа

МПа

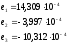
Тогда имеем:

МПа

МПа

МПа

МПа

3. Покажем напряжения на гранях куба (МПа)

Рисунок 7

8. Определение области деформирования

- интенсивность напряжений

МПа

МПа

а значит материал находится в области упругой деформации

9. Список использованной литературы

1. «Основы механики деформируемого твердого тела» Учебное пособие В.М.Волков; НГТУ. Н.Новгород, 2004 г.

2. Курс лекций по механике сплошных сред за 2013г.

23