На основании законов Булевой алгебры доказываются следующие свойства минтермов:

1. Сумма всех минтермов Булевой функции равна единице, то есть

2. Произведение любого числа минтермов с неодинаковыми индексами равняется нулю

3. Произведение всех макстермов равно нулю, то есть

4. Сумма любого числа макстермов с неодинаковыми индексами равняется единице

5. Минтерм с индексом i равняется инверсии макстерма с индексом 2ⁿ-i-1 и наоборот: ,.

Перейдем теперь к способам алгебраического представления функций Буля, используя выше приведенные понятия минтермов и макстермов.

Совершенная дизъюнктивная нормальная форма (СДНФ)

Покажем, что с помощью минтермов можно выразить любую логическую функцию. Рассмотрим, например, произвольную функцию двух аргументовf=f(x₁, x₂) и запишем ее в следующем виде:

(2.1)

легко убедиться в справедливости этой формулы простой подстановкой прямого и инверсного значений x₁.

Каждое слагаемое в (2.1) можно преобразовать аналогичным способом:

(2.2)

Подставляя соотношения (2.2) в формулу (2.1), получим:

(2.4)

Коэффициенты, стоящие перед функцией представляют собой не что иное, как минтермы этой функции при определенных значениях ее аргументов. Этот результат можно распространить на функцию Буля с любым числом аргументов. Так как функция принимает значения только нуля или единицы, то можно сделать следующий важный вывод:

Истинное (единичное) значение функции Буля можно представить в виде суммы минтермов на тех наборах аргументов, при которых она принимает единичное значение.Это и есть совершенная дизъюнктивная нормальная форма представления функции Буля:

(2.5)

Совершенная конъюктивная нормальная форма (СКНФ) . Воспользуемся формулой (2.5) для описания инверсных значений функции Буля:

(2.6)

.

Применим к правой части уравнения правило де- Моргана, возьмем инверсию от левой и правой частей и получим выражение для конъюнктивной нормальной формы описания Булевой функции:

(2.7)

Результат проведенного анализа можно сформулировать следующим образом: Истинное значение Булевой функции можно представить в виде произведения ее макстермов вида , где i- индекс макстерма, при котором функция f_i равняется нулю.

Приоритет в использовании СДНФ или СКНФ определяется рядом соображений, в числе которых: тип выбранных логических элементов, удобство проведения дальнейших логических преобразований, оптимальность схемотехнической реализации.

i	A	В	f
0	0	0	1
1	0	1	0
2	1	0	1
3	1	1	1

Таблица 2.9 Приведем простой пример алгебраической записи логической функции, представленной в таблице истинности 2.9:

Из формул (2.5) и (2.7) находим:

В форме СДНФ: f=m₀+m₂+m₃=

В форме СКНФ:

2.3.3.2 Представление Булевых функций в виде карт Карно

Карта Карно, или карта минтермов Булевой функции, представляет собой прямоугольную таблицу, разбитую на клетки по числу минтермов С=2ⁿ. Каждая клетка кодируется, причем кодирование осуществляется в коде Грея, относящимся к типу циклических кодов. Отличительная особенность этого кода состоит в том, что каждая последующая кодовая комбинация отличается от предыдущей значением только одного разряда. Правило формирования состояний кода Грея состоит в следующем: начинать надо из нулевого состояния, а потом для каждого следующего выбрать самый младший разряд, изменение которого приводит к образованию нового состояния, и взять его инверсное значение. Пример построения карт Карно, их кодирования и соответствия кода Грея прямому двоичному кодированию десятичных чисел применительно к функциям Буля трех, четырех и пяти переменных показан на рис.2.3, 2.4, 2.5.

Рис. 2.3

Рис. 2.5

В клетки карты Карно (рис. 2.4) помещены десятичные цифры от нуля до пятнадцати, что соответствует всем значениям двоичного четырехразрядного числа. Значения кодовых комбинаций старших разрядов АВ и младших СDуказаны рядом с картой по вертикали (для АВ) и по горизонтали (для СD) по правилам кода Грея. Легко убедиться, что два находящихся Рис. 2.4

рядом десятичных числа, например 5 и 6, коды Грея которых соответственно равны 0110 и 0101, отличаются только значением второго разряда, а в прямом двоичном представлении (0101 и 0110) эти же числа имеют различие в двух разрядах.

С целью записи и обработки Булевых функций клетки карты Карно заполняются значениями функции, соответствующими коду того или иного минтерма. Если же функция может принимать произвольное значение (в силу особенностей функционирования логического устройства), то клетка обычно отмечается знаком x. Приданиеxопределенного значения используется в дальнейших преобразованиях Булевой функции. Условимся в дальнейшем заполнять карту Карно только единичными и неопределенными значениями функции, оставляя пустыми те клетки, где функция по условию задачи равняется нулю (за исключением случаев, где это необходимо).

К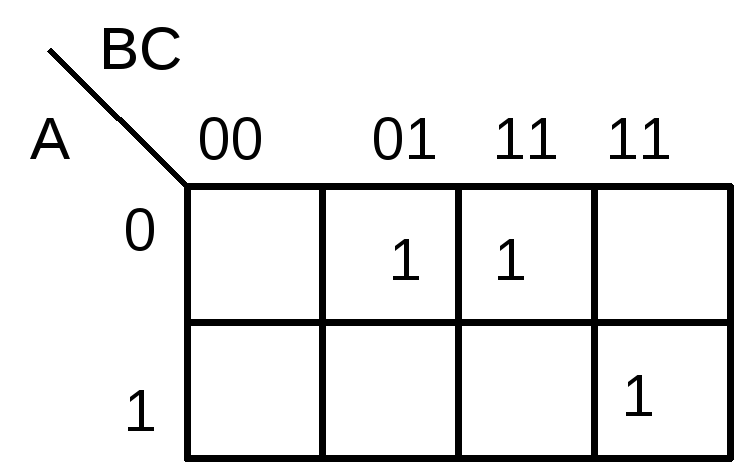арты Карно являются весьма удобным средством отображения Булевой функции, как это показано на рисунке 2.6, где в карте размещена функция трех переменных, представленная в СДНФ.

Аналогичным образом решается и обратная задача- списывание функции из карты.

Рис. 2.6