L. 513. «Электротехника» Аксютин В.А.

Примеры расчёта переходных процессов в цепях первого порядка.

Пример 1. Включение R L - цепи на постоянное напряжение.

Рассчитать закон изменения тока и напряжения на индуктивности, в R L - цепи (рис. 1а) при подключении её к источнику постоянного напряжения E.

Процесс описывается неоднородным обыкновенным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа

R i + L . = E.

а б

Рис. 1

1. Запишем общее решение искомого тока и напряжения:

i(t)= i _ПР(t)+ i_СВ(t) и u_L(t)= u _LПР(t)+ u_LСВ(t) (1)

а б

Рис. 2

2. Определим принуждённую составляющую искомого тока i _ПР(t) и напряжения u _LПР(t) по схеме замещения рис. 2а, для установившимся режима после коммутации при t=∞

i _ПР(t) = и u_LПР (t)=0. (2)

3. Находим свободную составляющую i_СВ(t) и u_{L СВ}(t).

Общее решение для i_СВ(t) и u_{L СВ}(t) можно записать после решения характеристического уравнения.

3.1. Составим характеристическое уравнение.

Для чего составляем схему замещения рис. 2б, относительно разрыва в любом месте после коммутационной цепи записываем входное сопротивление и, приравнивая его нулю, получим однородное уравнение:

Z_BX = R + p L = 0, определяем корень уравнения: р = – _. (3)

Записываем решение для свободной составляющей:

i _СВ(t) = Ae^pt и u_{L СВ}(t) = Be^pt. (4)

3.2. Определяем постоянные интегрирования A и B.

3.2.1. Записываем решение для тока i(t) и напряжения u_L(t) при t=0₊, с учётом (2) и (4) получим:

i(t)= i _ПР(t)+ i_СВ(t) = + Ae^pt, i(0) = + A, (5)

u_L(t)= u _LПР(t)+ u_LСВ(t) = 0+Be^pt, u_L(0) = 0+B. (6)

3.2.2. Определяем независимые начальные значения i(0₊) = i_L(0₊) = i_L(0_–)

До коммутации t=0_– ключ разомкнут, ток в цепи равен нулю и в цепи нулевые начальные условия:

i(0₊) = i_L(0₊) = i_L(0_–) = 0 (7)

3.2.3. Определяем зависимые начальные значения – u_L(0₊).

Составляем уравнение по второму закону Кирхгофа (рис. 1а) при t=0₊ :

E = R i(t) + u_L(t)..или E = R i(0₊) + u_L(0₊). (8)

Подставив (7) в (8) получим: u_L(0₊) = E.

3.2.4. Определяем постоянные интегрирования из (5) и (6) с учётом (7) и (8)

i(0) = + A = 0 и A = – , (9)

u_L(0) = 0+B = E и B = E. (10)

4. Записываем полное решение для i(t) и u_L(t) и строим графики процесса

i(t) = (1 – e^pt) =(1 – e^–t/τ). (11)

u_L(t)= E e^–t/τ. (12)

Кривые изменения тока i(t), и напряжения u_L(t) приведены на рис. 11б. Из графиков видно, что ток в цепи не устанавливается мгновенно и требуется определённое время до наступления установившегося тока i _ПР(t) = E / R. Напряжение на индуктивности до коммутации равно нулю, а в момент коммутации устанавливается скачком до значения u_L(0₊) = E и затем уменьшается до нуля.

В (11) и (12) τ = 1/|p|= R/L – называют постоянной времени, которая имеет размерность времени и может быть определена как время, в течение которого свободная составляющая уменьшается в e раз по сравнению со своим начальным значением i_СВ(0₊).

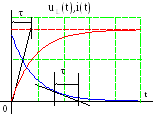
Постоянная времени t может быть определена по графикам i(t)или u_L(t). Она равна длине подкасательной к кривой, изменяющейся по экспоненциальному закону (рис. 3).

Рис. 3

Пример 2. Включение R L - цепи на переменное напряжение.

Рассчитать закон изменения тока и напряжения на индуктивности, в R L - цепи (рис. 1а) при подключении её к источнику синусоидального напряжения

e(t) = E_m sin(ωt + Ψ)

R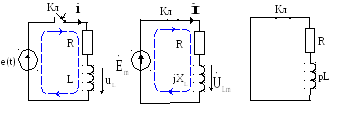 i + L . = e(t). (1)

а б в

Рис. 1

Процесс описывается неоднородным обыкновенным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа

1. Запишем общее решение искомого тока и напряжения:

i(t)= i _ПР(t)+ i_СВ(t) и u_L(t)= u _LПР(t)+ u_LСВ(t) (2)

2. Определим принуждённую составляющую искомого тока i_ПР(t) и напряжения u_LПР(t). Применим символический метод. Схема замещения для установившимся синусоидального режима после коммутации (t=∞ ) приведена на рис. 1б.

• Комплекс амплитудного значения ЭДС: = E_m e^jΨ

• Индуктивное сопротивление: X_L =  L

• Комплексное сопротивление: Z = R + j X_L= Z e^jφ

где Z = и φ = arc tg

• Комплекс амплитудного значения принуждённого тока:

= = = e^j(Ψ-φ) = I_m e^j(Ψ-φ) , (3)

где I_m = .

• Комплекс амплитудного значения принуждённого напряжения:

= j X_L.= e^j(Ψ-φ) X_L e^j90 = X_L e^j(Ψ-φ+90) = U_Lm e^j(Ψ-φ+90) , (4)

где U_Lm = X_L .

• Мгновенные значения принуждённого тока:

i _ПР(t) = I_m sin(ωt + Ψ – φ). (5)

• Мгновенные значения принуждённого напряжения на индуктивности:

u _LПР(t) = U_Lm sin(ωt + Ψ – φ + 90°). (6)

3. Находим свободную составляющую iСв(t) и uL св(t).

Общее решение для i_СВ(t) и u_{L СВ}(t) можно записать после решения характеристического уравнения.

3.1. Составим характеристическое уравнение.

Для чего составляем схему замещения рис. 1в, относительно разрыва в любом месте после коммутационной цепи записываем входное сопротивление и, приравнивая его нулю, получим однородное уравнение:

Z_BX = R + p L = 0, определяем корень уравнения: р = – _. (7)

Определяем постоянную времени τ = 1/|p|= R/L.

Записываем решение для свободной составляющей:

i _СВ(t) = A e^pt = A e^–t/τ и u_{L СВ}(t) = B e^pt = B e^–t/τ . (8)

3.2. Определяем постоянные интегрирования a и b.

3.2.1. Записываем решение для тока i(t) и напряжения u_L(t) при t=0₊, с учётом (5) и (6) получим:

i(t)= i _ПР(t)+ i_СВ(t) = I_m sin(ωt + Ψ – φ)+ A e^–t/τ,

i(0) = I_m sin(Ψ – φ)+ A, (9)

u_L(t)= u _LПР(t) + u_LСВ(t) = U_Lm sin(ωt + Ψ – φ + 90°) + B e^–t/τ ,

u_L(0) = U_Lm sin( Ψ – φ + 90°) + B. (10)

3.2.2. Определяем независимые начальные значения i(0₊) = i_L(0₊) = i_L(0_–)

До коммутации t=0_– ключ разомкнут, ток в цепи равен нулю и в цепи нулевые начальные условия:

i(0₊) = i_L(0₊) = i_L(0_–) = 0 (11)

3.2.3. Определяем зависимые начальные значения – u_L(0₊).

Составляем уравнение по второму закону Кирхгофа для после коммутационной цепи (рис. 1а):

e(t) = E_m sin(ωt + Ψ – φ) = R i(t) + u_L(t).

при t=0₊ E_m sin( Ψ) = R i(0₊) + u_L(0₊). (12)

u_L(0₊) = E_m sin( Ψ) .

3.2.4. Определяем постоянные интегрирования из (9) и (10) с учётом (11) и (12)

i(0) = I_m sin(Ψ – φ)+ A = 0,

A = – I_m sin(Ψ – φ), (13)

u_L(0) = U_Lm sin( Ψ – φ + 90°)+B = E_m sin( Ψ),

B = E_m sin(Ψ) – U_Lm sin(Ψ – φ + 90°). (14)

4. Записываем полное решение для I(t) и uL(t) и строим графики процесса.

i(t) = I_m sin(ωt + Ψ – φ) – I_m sin(Ψ – φ) e^–t/τ. (15)

u_L(t)= U_Lm sin(ωt + Ψ – φ + 90°) +[E_m sin(Ψ) – U_Lm sin(Ψ – φ + 90°)] e^–t/τ. (16)

Пусть заданы значения: R=10 Ом; L= 0.15; Гн;

E_m = 100 В; f = 100 Гц; Ψ =22.5°.

Подставив значения исходных данных в (3), (4), (7), (15) и (16) получим:

I_m = 1.055A; U_Lm = 99.4B; p = – 99.4 c^-1

φ = 83.9°; A = 0.927 A; B = – 0.9267 B

i(t) = 1.055 sin(628 t – 61.42°) + 0.927 e^–66.7t.

Рис. 2

u_L(t) = 99.4 sin(628 t + 28.58°) – 9.268 e^–66.7t.

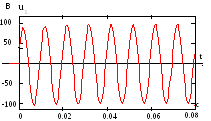
Рис. 3

Кривые изменения тока i(t) и напряжения u_L(t) приведены на рис. 2 и рис. 3. Из графиков видно, что синусоидальный процесс для тока устанавливается в течении нескольких колебаний синусоиды и в течении этого времени возможны значительные броски тока.

Из (14) видно, что при Ψ – φ = 0, A = 0 и переходный процесс в цепи не возникает.

Пример 3. Включение последовательной RC - цепи на постоянное напряжение

Рассчитать закон изменения тока и напряжения на ёмкости, в R C - цепи (рис. 1а) при подключении её к источнику постоянного напряжения E.

Процесс описывается неоднородным обыкновенным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа

R i (t)+ u_C(t) = E. (1)

С учетом i (t) = C получается

RC + u_C(t) = E.. (2)

а б

Рис. 1