1H1, 2He4, 3Li7, 11Na23, 37Rb87.

При сверхнизких температурах атомы находятся в основном состоянии, первые два имеют нулевой спин, а у последних трех спин равен единице. Число спиновых состояний

.

Число атомов сохраняется, поскольку сохраняется барионное число нуклонов.

Число частиц газа. Из распределения Бозе–Эйнштейна

и плотности состояний трехмерного газа (3.8)

, ,

получаем число частиц с энергией в интервале

. (4.77)

Полное число частиц

. (4.78)

Химический потенциал. При изменении температуры число частиц (4.78) сохраняется, тогда степень экспоненты не зависит от T

, (4.78а)

где учтено . Следовательно, при уменьшении температуры уменьшается ||, и химический потенциал увеличивается от отрицательных значений до нуля, достигая его при . Привыполняется

. (4.79)

Дальнейший рост μ невозможен и при последующем понижении температуры (4.78а) выполняется за счет уменьшения числа частиц N.

Порог конденсации – это верхняя граница интервала, где химический потенциал равен нулю:

.

Из (4.78) получаем

.

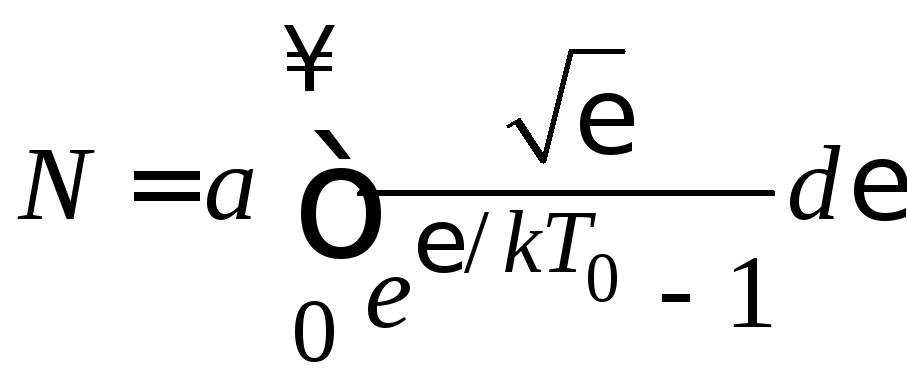Используя

,

вычисляем интеграл

,

находим

,

. (4.80)

Температура порога конденсации возрастает с увеличением концентрации атомов и с уменьшением массы атома.

Массу атома выражаем через молярную массу, концентрацию атомов – через молярный объем

, .

Из (4.80) в системе единиц СГС получаем

[К]. (4.81)

Для ₂He⁴:

, ,,.

Найдем длину волны де Бройля атома на пороге конденсации. Для атома со средней энергией

и средним импульсом

из (4.80) получаем

,

.

Учитывая , гдеd – среднее расстояние между атомами, находим

.

При понижении температуры длина волны де Бройля атома увеличивается и при достижении порога конденсации сравнивается с расстоянием между атомами. Волновые функции соседних атомов перекрываются и интерферируют.

Число конденсированных частиц при температуре T. В интервале температур химический потенциал равен нулю. При понижении температуры нижеТ₀ уравнение (4.78) с для числа частиц в газовой фазе

выполняется за счет уменьшения числа частиц газовой фазы от первоначального N до текущего N₁(Т). Аналогично (4.80)

получаем

, .

Делим на (4.80) и находим число и концентрацию частиц, оставшихся при в газовой фазе:

, (4.82)

. (4.82а)

Число конденсированных частиц

. (4.83)

Относительное число частиц конденсированной фазы как функция температуры показано на рисунке пунктиром, газовой фазы– сплошной линией.

Внутренняя энергия и теплоемкость. Используя число частиц (4.77)

,

получаем внутреннюю энергию

, (4.84)

где . Ниже порога конденсации находим

или

, (4.85)

где

.

Внутренняя энергия определяется вкладом лишь газовой фазы, внутренняя энергия конденсированной фазы равна нулю. Из (4.85) и (4.82) находим энергию, приходящуюся на частицу газовой фазы ниже порога конденсации:

. (4.86)

Из (4.85) находим теплоемкость ниже порога конденсации:

. (4.87)

Учитывая (4.80)

,

из (4.87) получаем теплоемкость при температуре конденсации

. (4.87а)

Свободная энергия следует из (4.85) и из уравнения Гиббса–Гельмгольца (2.29)

. (4.88)

Энтропия и давление выражаются через свободную энергию согласно (2.33), тогда в области конденсации

, (4.89)

,

. (4.90)

Выражение (4.90) является уравнением состояния нерелятивистского идеального квантового газа. Сравнивая (4.89) и (4.82)

,

находим, что энтропия пропорциональна числу частиц газовой фазы. Следовательно, энтропия конденсированной фазы равна нулю. Давление определяется температурой и не зависит от объема. Конденсированные частицы имеют нулевой импульс, не создают давления, конденсированная фаза абсолютно сжимаема. При давление пропорционально концентрации частиц газовой фазы, равной (4.82а), тогда

. (4.91)