Фононный газ

Тепловое движения частиц в кристалле вызывает распространение по решетке упругих волн. При взаимодействии с преградой волна передает ей энергию квантом – фононом. Название от др.-греч.  – «звук» дал Френкель в 1932 г. С каждой упругой волной связан набор фононов. Фононы всех волн в кристалле образуют фононный газ. Основы квантовой статистической теории кристаллической решетки заложили Эйнштейн в 1907 г. и Дебай в 1912 г.

Альберт Эйнштейн (1879–1955) Петер Дебай (1884–1966)

Акустические и оптические волны в кристалле. Волна – это колебательный процесс, распространяющийся в пространстве, когда колебание одного узла передается соседнему узлу. Если в элементарной ячейке находятся r частиц и число ячеек N, то трехмерный кристалл имеет 3rN степеней свободы – независимых типов движения. Каждой степени свободы соответствует своя волна. Число независимых волн

,

где исключены 6 степеней свободы, связанных с поступательным и вращательным движением кристалла как целого. Из общего количества выделяются 3N волн, имеющих достаточно малую частоту и называемых акустическими. При их распространении элементарная ячейка колеблется как единое целое и далее называется узлом кристалла. Зависимость частоты от волнового числа при маломk близка к линейной. Остальные волн имеют высокие частоты, обычно находящиеся в инфракрасной области спектра и называемыеоптическими. Они вызывают колебания частиц ячейки друг относительно друга, зависимость оказываетсянелинейной. Оптические волны возбуждаются при сравнительно высокой температуре. Далее ограничиваемся акустическими волнами.

Закон дисперсии волны связывает частоту волны ω и волновое число k. Получим для одномерной цепочки атомов, между которыми действует упругая сила, и колебания происходят в продольном направлении.

В стационарных состояниях атомы расположены на равных расстояниях d друг от друга и показаны на рисунке темными кружками. В возмущенном состоянии атом n сдвинут на расстояние и показан серым кружком. Со стороны соседнего атома, находящегося справа, действует упругая сила с проекцией на осьx

,

где  – коэффициент жесткости связи; – увеличение расстояния между атомами. Для атома n получаем силу

.

Второй закон Ньютона дает уравнение

.

Решение ищем в виде волны

,

где nd – положение атома n. Подставляем в уравнение

.

Получаем закон дисперсии

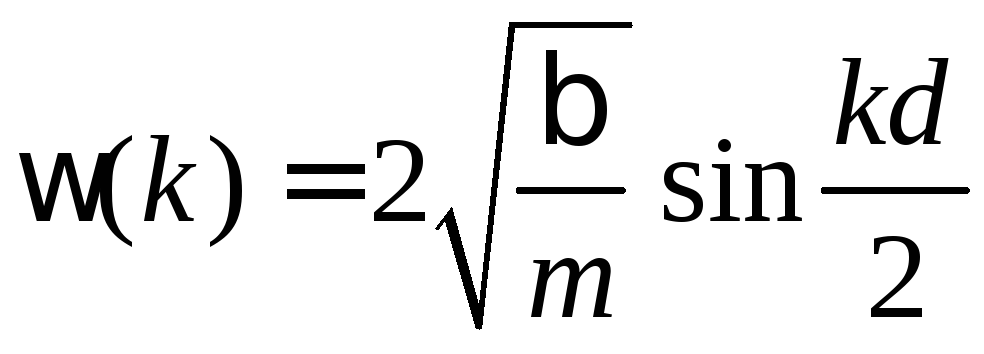. (П.1)

Функция показана на рисунке, где знакиволнового числаk соответствуют противоположным направлениям волны.

Входящие в (П.1) величины ограничены значениями:

частота колебаний – ,

волновое число –.

Тогда длина волны ограничена снизу

, . (П.2)

Для минимальной длины волны получаем закон колебаний

.

Для соседних атомов находим

, ,, ...

Следовательно, при максимальном волновом числе и минимальной длине волны соседние атомы колеблются в противофазе, бегущая волна превращается в стоячую волну, энергия не переносится по кристаллу. Аналогичная ситуация возникает для электрона на границе зоны Бриллюэна.

Для длинных акустических волн

,

из (П.1)

находим линейный закон дисперсии

, (П.3)

где – скорость волны. Для акустических волн выполняется линейный закон дисперсии.

Химический потенциал и распределение фононов по частоте. По аналогии с фотоном, упругой волне с частотой  сопоставляем набор фононов. Импульс и энергия фонона определяется длиной и частотой волны

, .

В кристалле существуют три независимых типа волн – одна продольная волна и две поперечных волны. По аналогии с фотоном каждому типу волны сопоставляем определенную проекцию спина фонона, тогда его спин равен 1 и фонон являются бозоном. Аналогично фотону, фонон не обладает каким-либо сохраняющимся зарядом, поэтому число фононов в кристалле не сохраняется и зависит от температуры. Для равновесного фононного газа

.

Из распределения Бозе–Эйнштейна для волны с частотой  получаем среднее число фононов

.

Плотность состояний в модели Дебая. Плотность состояний, или число волн в единичном интервале энергии, определяется законом дисперсии . В трехмерном кристалле каждый тип упругих волнраспространяется со своей скоростью v_m. Для акустических волн используем линейное приближение Дебая

,

соответствующее модели кристалла в виде упругого непрерывного тела. Модель применима для частот до ~ 10¹³ Гц.

Для линейного закона дисперсии плотность состояний, или число независимых волн в единичном интервале частот, получено в (П.8.10)

,

где средняя по типам поляризации скорость волн

.

Частота Дебая _D равна наибольшей частоте волны в кристаллической решетке. Ограничение на длину волны , полученное в (П.2) для закона дисперсии (П.1), связано с тем, что длина волны не может быть меньше удвоенного расстояния между узлами решетки. Физический смысл ограничения следует из рисунка, где серые кружки показывают атомы, смещенные под действием поперечной волны.

Точное значение _D для линейного закона дисперсии (П.3) получаем из условия – число волн в кристалле равно числу степеней свободы кристалла. Каждый из N узлов кристалла совершает колебания по трем независимым направлениям тогда число степеней свободы макроскопического кристалла . Число волн равно числу состояний, которое выражается через плотность состояний:

.

Находим частоту Дебая

, (4.69)

где N – число узлов в объеме V кристалла; v – средняя скорость волн.

Установим физический смысл результата. Один узел занимает объем

,

где d – постоянная решетки. Из (4.69) получаем

. (4.69а)

Наименьшая длина волны

согласуется с (П.2)

.

Из (4.69) выражаем среднюю скорость волн через частоту Дебая

.

Плотность состояний в трехмерном кристалле

выражаем через частоту Дебая

, (4.70)

где N – числом узлов кристалла. Функция плотности состояний для Al, полученная экспериментально, приведена на рисунке сплошной линией, приближение Дебая с показано пунктиром. Различие кривых обусловлено оптическими модами, присутствующими в реальном кристалле.

Тепловая часть внутренней энергии кристалла равна энергии фононного газа. С учетом энергии фонона и (4.70) получаем

.

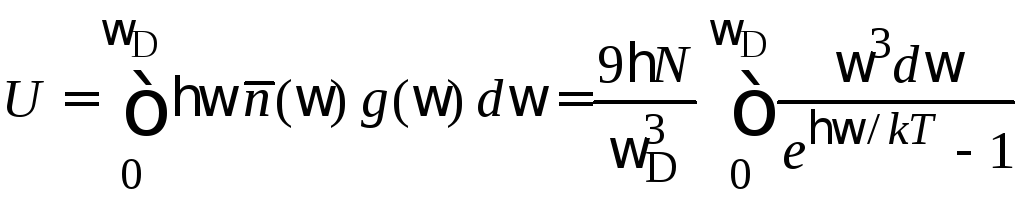Заменяем и находим

, (4.71)

где

. (4.71а)

Температура Дебая соответствует тепловой энергии, равной наибольшей возможной энергии фонона. В (4.71а) подставляем (4.69)

. (4.72)

Температура Дебая пропорциональна скорости волны v и обратно пропорциональна постоянной решетки. Скорость продольных волн

зависит от модуля Юнга Е и от плотности  кристалла. Скорость звука в кристалле порядка 1÷10 км/с и тем больше, чем прочнее вещество. Различают прочные и малопрочные кристаллы в зависимости от их температуры Дебая.

Крис-талл	C (алмаз)	Be	Si	Fe	Al	Cu	Ag	Au	Na	Pb	Hg
TD, К	2230	1440	645	470	428	343	225	165	158	105	72
, 10–2эВ	19,2	12,4	5,6	5,0	3,7	3,0	1,9	1,4	1,4	0,9	0,6
	Прочные Малопрочные

Наибольшая энергия фонона гораздо меньше энергии Ферми электрона в металле

.

При высокой температуре кристалла возбуждены все моды колебаний и выполняются законы классической физики. При низкой температуревысокочастотные моды не возбуждаются, «вымерзают», и существенны квантовые свойства.

Теплоемкость при высокой температуре. Для малопрочных кристаллов лабораторная температура удовлетворяет . Верхний предел интеграла (4.71)

меньше единицы, тогда . Экспоненту разлагаем в ряд, ограничиваемся двумя слагаемыми

,

получаем

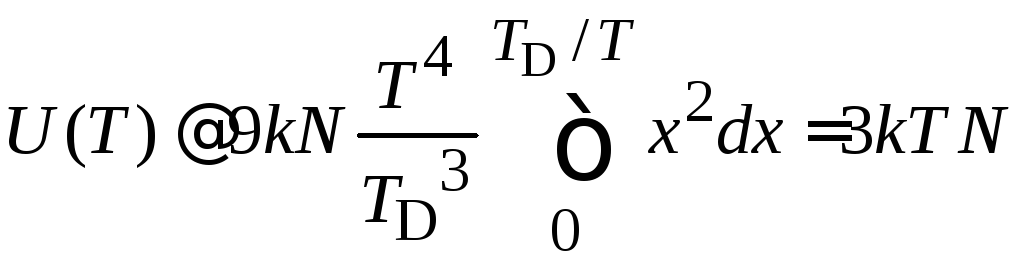. (4.73)

Теплоемкость

удовлетворяет закону Дюлонга–Пти классической физики.

Теплоемкость при низкой температуре. Для прочных кристаллов выполняется . Верхний предел интеграла (4.71) с экспонентой

считаем бесконечным. Используем

, ,,

получаем внутреннюю энергию кристалла

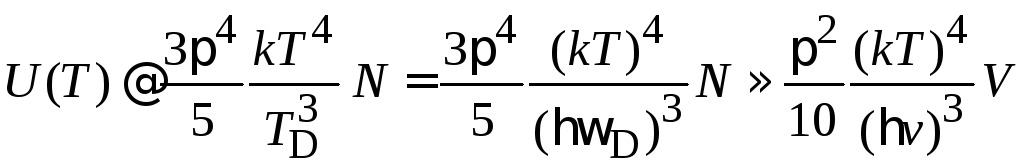. (4.74)

Результат аналогичен внутренней энергии фотонного газа (4.63) в виде закона Стефана–Больцмана

, .

Для теплоемкости кристаллической решетки прочных кристаллов получаем закон Дебая

. (4.75)

При низких температурах теплоемкость кристалла пропорциональна третьей степени температуры.

Теплоемкость для широкого интервала температур. Используем (4.71)

,

,

,

и получаем

. (4.76)