Одномерный электронный газ

В квантовой проволоке находится газ нерелятивистских электронов. Получим распределение электронов по энергии и химический потенциал.

Закон дисперсии частицы в квантовой проволоке, расположенной вдоль оси z:

, .

Считаем проволоку тонкой, концентрацию электронов низкой, в результате все электроны находятся в нижней зоне поперечного квантования с энергией . Температуру проволоки считаем настолько малой, что переходы на следующий уровень под действием теплового движения маловероятны

, .

Распределение электронов по энергии. Плотность состояний на единице длины проволоки ниже второй зоны получена в (П.8.6)

, .

Число электронов на единице длины проволоки в интервале энергии равно

. (4.41)

Линейную концентрацию находим интегрированием. Учитывая быстрое убывание функции распределения с ростом энергии, верхний предел считаем бесконечным, тогда число электронов на единице длины

. (4.42)

В интеграле заменяем ,и получаем

.

Вырожденный газ. При низкой температуре

вычисляем интеграл, используя разложение Зоммерфельда:

.

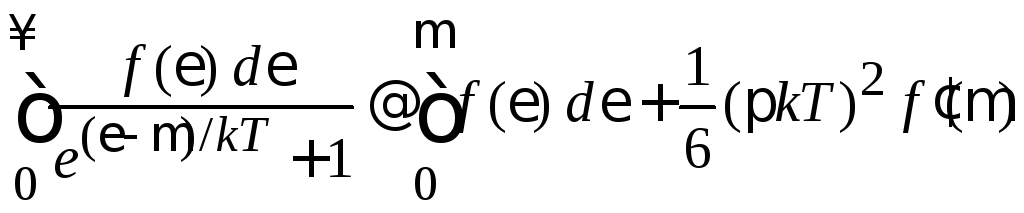При находим

.

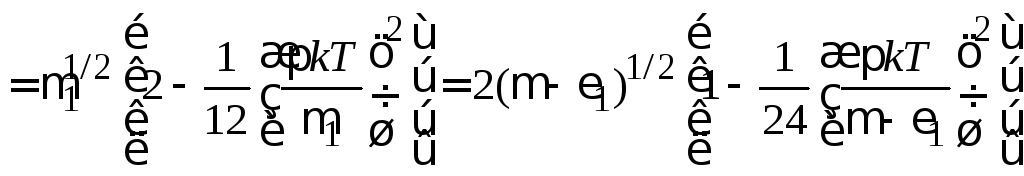Подстановка в (4.42)

дает

.

Возводим в квадрат

.

Используя

при ,

упрощаем квадратную скобку,

. (4.43)

Учтено, что из (4.43) при следует

. (4.43а)

Энергия Ферми увеличивается с ростом линейной концентрации и с уменьшением массы частицы. Полагаем в знаменателе второго слагаемого (4.43)

, (4.43б)

находим

. (4.43в)

Химический потенциал увеличивается с ростом температуры.

Условие вырождения газа с учетом (4.43а)

ограничивает температуру

. (4.44)

Условие нахождения электронов в нижней зоне

,

с учетом (4.43а) дает

,

и ограничивает сверху линейную концентрацию

. (4.45)

Для вырожденного газа с учетом (4.44) и (4.45) получаем

,

. (4.46)

Если спектр поперечных движений близок к спектру двухмерной, бесконечно глубокой потенциальной ямы с прямоугольным поперечным сечением , тогда

.

При a > b находим и, тогда из (4.45) получаем условие нахождения электронов в нижней зоне

.

Импульс Ферми. Из (4.43а)

находим

. (4.47)

Самая короткая длина волны де Бройля в газе

.

Учитывая

,

где d – характерное расстояние между частицами, получаем

.

Следовательно, волновые функции соседних частиц перекрываются, существенна интерференция между частицами, и газ вырожденный.

Кондактанс баллистического проводника

Кондактанс G (от англ. conductance – проводимость) – полная проводимость проводника, величина обратная сопротивлению

, ,

. (4.62)

Баллистический проводник (от греч. βάλλω – бросать) имеет протяженность, меньшую длины свободного пробега, и электроны пролетают его без рассеяния. Это происходит, например, при комнатной температуре в углеродных нанотрубках диаметром 5–25 нм, длиной до 10 мкм или в гетероструктуре GaAs–AlGaAs длиной до 100 мкм, при температуре 0,5 К с двумерным электронным газом в слое толщиной 5 нм. Отсутствие рассеяния зарядов не означает обращения сопротивления в нуль. Сопротивление баллистического проводника вызвано ограниченностью объема фазового пространства состояний, переносящих ток. Ограниченность обусловлена концами баллистического проводника, где он соединяется с обычным проводником, там и возникает сопротивление. В пределах баллистического проводника падение напряжения отсутствует.

Кондактанс баллистического проводника не зависит от материала проводника и его длины, а зависит от поперечного размера, сравнимого с длиной волны де Бройля. Кондактанс пропорционален числу поперечных мод, т. е. независимых видов поперечного движения, и выражается через мировые постоянные формулой Ландауэра (1970 г.).

Рольф Ландауэр (1927–1999)

Известен также принцип Ландауэра (1961 г.) – стирание 1 бита информации в памяти вычислительной системы приводит к выделению тепла

.

При выделяется. Эта минимальная энергия необходима для обработки 1 бита информации и равна высота барьера, разделяющего два состояния электрона в устройствах электронной памяти.

Эффективный поперечный размер и кондактанс можно изменять электрическим полем затвора. Такое устройство – квантовый точечный контакт предложил Юрий Васильевич Шарвин в 1965 г. Он же впервые исследовал баллистический проводник.

Формула Ландауэра. Баллистический проводник соединен с термодинамически равновесными контактами 1 и 2, на которые подана разность потенциалов U. В контактах при низкой температуре состояния заполнены электронами до уровней Ферми и. Напряжение создает электрохимические потенциалы электронного газа в контактах

,

и вызывает в проводнике электрический ток. Каждое состояние ниже уровня Ферми заполнено одним электроном. Число электронов , прошедших проводник, равно числу состояний n одномерного движения с учетом кратности вырождения

,

где учитывает две проекции спина электрона и–число поперечных мод проводника, то есть уровней поперечного квантования. В результате

.

Найдем число состояний n одномерного движения.

Распределения электронов в сообщающихся контактах

при низкой температуре

Каждое состояние одномерного движения занимает фазовый объем h, тогда число состояний

.

Для получения фазового объема дифференцируем

,

находим

.

Для электронов, прошедших проводник

, ,

тогда фазовый объем

,

где

– время движения электрона по проводнику. В результате число прошедших электронов

.

Проходящий заряд создает ток

. (4.63)

Для сопротивления и кондактанса между контактами 1 и 2 при низкой температуре получаемформулу Ландауэра

, . (4.64)

Величины не зависят от длины и материала проводника. Для одномодового баллистического проводника

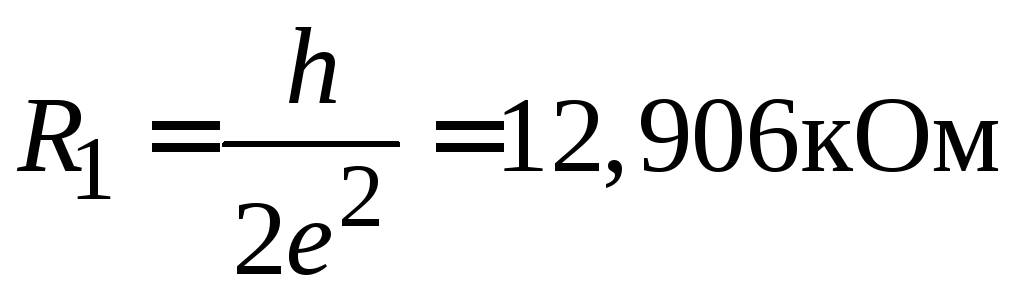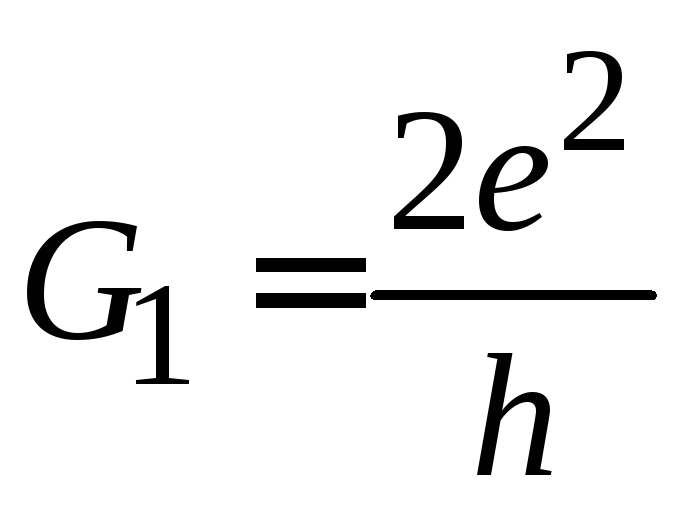, . (4.64а)

Величина равна кванту сопротивления (1.36), рассмотренному ранее. Множитель 2 связан с двумя проекциями спина электрона.

Проводимость при конечной температуре. Распределение электронов

зависит от температуры. Ток из одного контакта заполняет электронами свободные состояния в другом контакте, и вместо (4.63)

получаем

, .

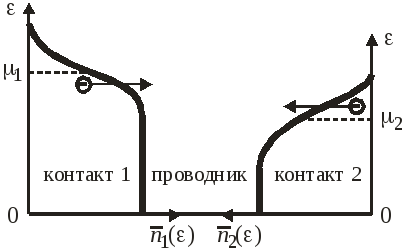
При малом различии между химическими потенциалами разлагаем разность распределений в ряд Тейлора, и оставляем первое слагаемое

.

В результате получаем

,

. (4.65)

С учетом (4.8в)

область интегрирования (4.65) находится вблизи уровня Ферми.

Число поперечных мод равно числу видов движений, перпендикулярных проводнику и отличающихся длиной волны. На непроницаемых стенках проводника волновая функция в виде стоячей волны имеет узлы, и на поперечном сечении проводника ширинойd укладывается целое число полуволн, тогда

.

При низких температурах активизированы состояния около уровня Ферми. Энергия частицы складывается из энергий поперечногои продольногодвижений, тогда

.

С учетом

,

находим минимальную длину волны, соответствующую и равную

.

Рост увеличивает. Перераспределение энергиимежду продольным и поперечным движением создает число поперечных мод

, (4.66)

где […] означает целую часть. Чем шире проводник, тем больше поперечных мод при фиксированной энергии Ферми. Для полевого транзистора шириной сполучаеми.

На сочленениях цепи, где широкий резервуар соприкасается с узким проводником, моды перестраиваются, меняется их длина волны и число. Сопротивление баллистического проводника, находящегося между резервуарами, вызвано перестройкой поперечных мод в местах сочленения. Если они симметричные, то, согласно (4.65) , каждое сочленение с одномодовым проводником создает сопротивление

.

Приложенное напряжение падает на сочленениях, как показано на рисунке.

Для проводника шириной d из (4.64) для одной проекции спина кондактанс , и из (4.66)получаемпроводимость Шарвина

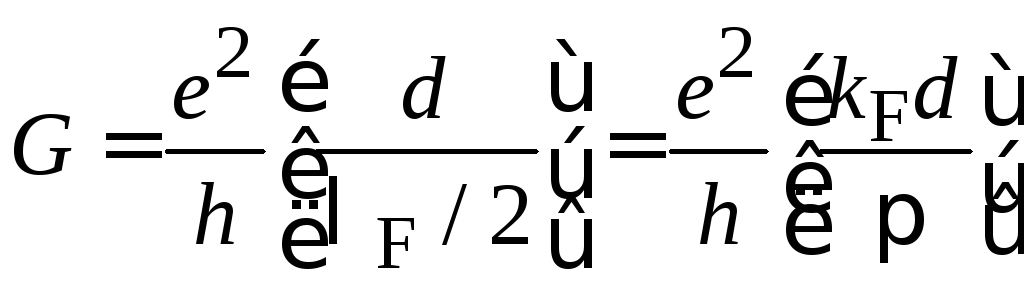. (4.67)

Увеличение ширины проводника повышает проводимость скачком на каждый раз, когда появляется очередная мода, т. е. при выполнении

. (4.68)

где – целое число.

В эксперименте 1988 г. Wees и Houten изменялось число поперечных мод электронного газа в гетероструктуре , показанной на рис.а. Двухмерный электронный газ изображен серой полосой 2. Газ соединен с резервуарами электронов 1 и 5. Параметры газа: ;; концентрация электронов; длина свободного пробега. На электроды 3 и 4, расположенные над слоем на расстоянии друг от друга, подается одинаковый и варьируемый потенциал. Электроды образуютрасщепленный затвор. Поле затвора «выдавливает» электроны газа из области вблизи электродов и сужает область, доступную для движения по оси y.

а б

(а) – контакт с расщепленным затвором 3-4,

(б) – зависимость кондактанса от ширины контакта по осиy,

Образуется квантовый точечный контакт, контролирующий число поперечных мод путем вариации эффективной ширины контакта d. Зависимость кондактанса от d при показана на рисункеб сплошной линией. При монотонном росте d каждый раз, когда достигается выполнение (4.68), величина кондактанса увеличивается скачком на . Шаг эффективной ширины в проведенном эксперименте составлял. При повышении температуры уровень Ферми и размываются, ступени графика получают наклон, показанный пунктиром. При , где – энергия поперечного квантования, ступени графика сглаживаются, он превращается в прямую линию, соответствующую классической зависимости – проводимость пропорциональна ширине проводника.