Электронный газ металла и полупроводника

В узлах кристаллической решетки металла находятся положительные ионы. Волновые функции валентных электронов соседних атомов перекрываются. Межатомное взаимодействие приводит к расщеплению верхних уровней на множество подуровней. Каждый уровень создает зону с квазинепрерывным спектром. В результате валентные электроны перемещаются по кристаллу, образуя идеальный газ квазичастиц, характеризующихся эффективной массой. При отсутствии магнитного поля на каждом подуровне могут быть 0, 1 или 2 электрона, отличающиеся проекциями спина.

Трехмерный электронный газ

Распределение электронов по энергии. В единице объема, в единичном интервале энергии около значения , находится число электронов

. (4.21)

Плотность состояний в единице объема (3.8а)

, ,

и распределение Ферми

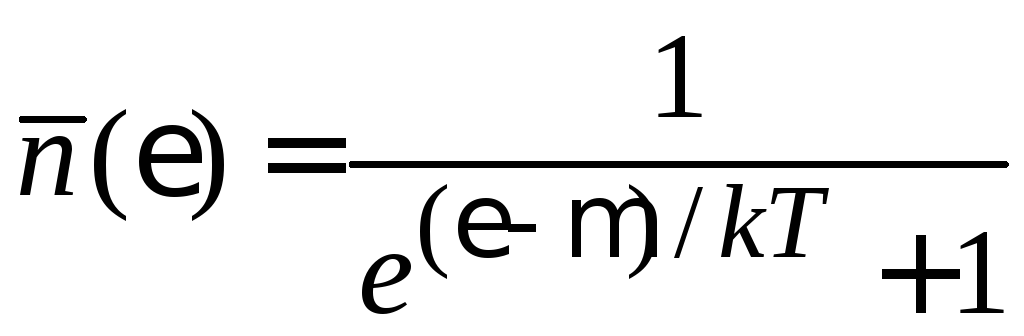
дают

. (4.21а)

Площадь под кривой равна концентрации электронов

.

Энергия, импульс и температура Ферми. При получаем

, ,

, .

Концентрация электронов и энергия Ферми

,

,

, (4.22)

плотность состояний в единице объема на уровне Ферми

. (4.23)

Для типичного металла постоянная решетки, концентрация электронов, энергия Ферми и плотность состояний

, ,

,

.

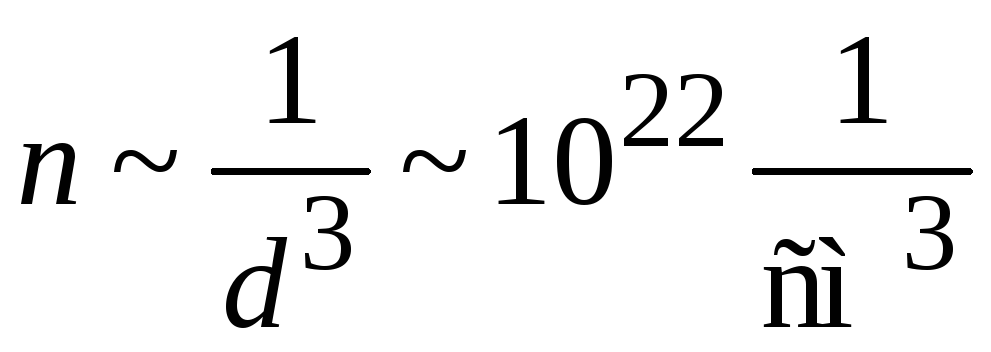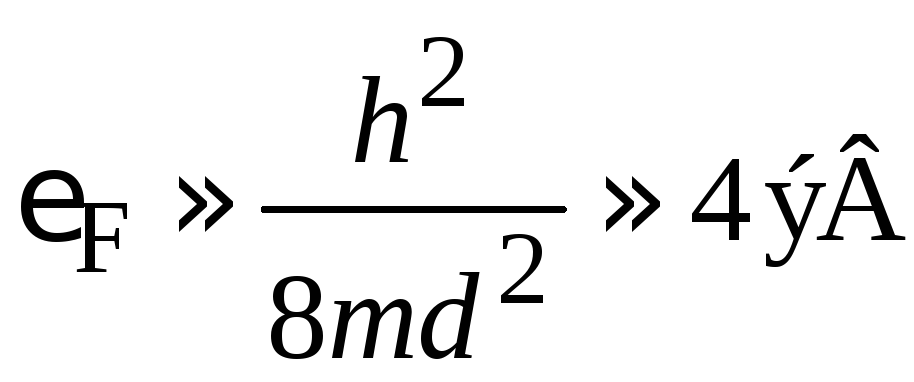Импульс Ферми равен наибольшему импульсу электрона в газе при абсолютном нуле температуры

, (4.24)

скорость Ферми

.

Принцип Паули препятствует размещению частиц в области фазового пространства с малыми значениями импульса, которая уже занята другими частицами, поэтому p_F увеличивается с ростом концентрации частиц.

Если бы принцип Паули перестал действовать, то для получения энергии Ферми потребовалась бы температура, называемая температурой Ферми:

. (4.25)

Сравниваем ее с критической температурой вырождения (4.19а)

,

и получаем

.

Для металлов первой группы таблицы Менделеева

Металл	n, 1022 см–3	m/m0	F, эВ	TF, 104К
Na Cs Cu Ag	2,5 0,91 8,45 5,85	1,0 0,98 0,99 1,01	3,24 1,58 7,00 5,48	3,77 1,83 8,12 6,36

Лабораторная температура

,

и электронный газ металлов вырожденный.

Поверхность Ферми является поверхностью постоянной энергии в пространстве квазиимпульса

.

Эта поверхность ограничивает область состояний, занятых электронами при , от области, где нет электронов.Для свободного электронного газа поверхность Ферми является сферой радиусом

.

Приблизительно форму сферы имеет поверхность Ферми щелочных металлов Na, K, Rb, Cs, у которых достаточно велико расстояние от сферы Ферми до края первой зоны Бриллюэна. В общем случае поверхность Ферми в кристалле имеет многосвязную форму, вызванную дифракцией и интерференцией волны де Бройля в кристаллической решетке.

Ферми-поверхность металлов Na, Cu, Ca

Граница зоны Бриллюэна на рисунке имеет форму многогранника.

Собственная проводимостЬ полупроводника

Полупроводник при имеетзону проводимости свободную от электронов и полностью заполненную валентную зону, отделенную запрещенной зоной шириной . В валентной зоне отсутствуют свободные места, куда могли бы переместиться заряды, в зоне проводимости зарядов нет. В результате полупроводник является изолятором.

При тепловое движение перебрасывает электроны через запрещенную зону, в зоне проводимости появляются электроны, в валентной зоне – вакантные места –дырки.

При термодинамическом равновесии химические потенциалы электронов и дырок равны. Энергию отсчитываем от края валентной зоны.

Зона проводимости . Кинетическая энергия электрона

.

Плотность состояний (3.8) единицы объема трехмерного газа

.

Концентрация электронов n_e мала, газ невырожденный, используем распределение Максвелла

.

Из

,

находим число электронов в единице объема с энергией в интервале

. (П.10.4)

Концентрация электронов со всеми энергиями в пределах зоны проводимости

.

В интеграле заменяем аргумент и интегрируем

,

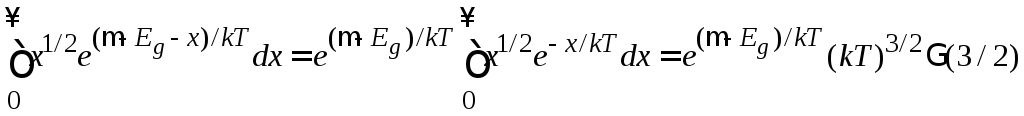где использовано

.

Получаем концентрацию электронов в зоне проводимости

, (П.10.5)

где

.

Для Si при :

, , .

Эффективную массу электрона выражаем через концентрацию электроновпри помощи (П.10.5)

.

Подставляем в (П.10.4) и находим число электронов в единичном интервале энергии зоны проводимости

. (П.10.4а)

Результат совпадает с распределением Максвелла по энергии. График показан пунктиром на рисунке.

Валентная зона  < 0,

.

Плотность состояний (3.8) дырок h (от англ. hole – «дырка»)

.

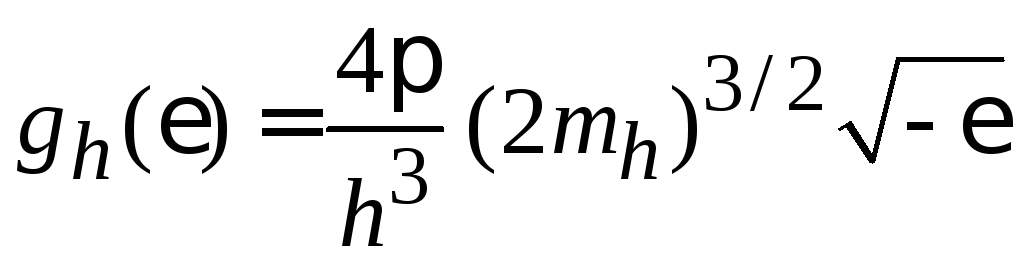Дырка – это не заполненное электроном состояние валентного уровня. В валентной зоне среднее число электронов и дырок в одном состоянии

.

Из распределения Ферми–Дирака для электронов

получаем распределение Ферми–Дирака для дырок

.

Сравнение распределений ипоказывает, чтохимические потенциалы электронов и дырок противоположны по знаку. Концентрация дырок мала, газ невырожденный, пренебрегаем единицей в знаменателе, получаем распределение Максвелла для дырок

.

В результате

. (П.10.6)

Интегрируем по энергии в пределах валентной зоны

.

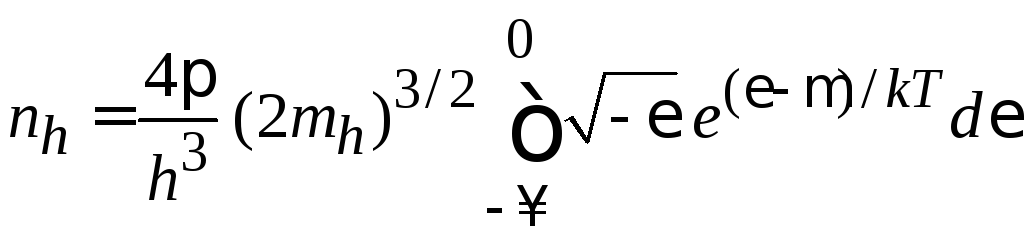Заменяем

,

получаем концентрацию дырок в валентной зоне

, (П.10.7)

где

.

Эффективную массу дырки выражаем через концентрацию дырок при помощи (П.10.7)

.

Подставляем в (П.10.6) и находим число дырок в единичном интервале энергии валентной зоны

. (П.10.6а)

График распределения показан пунктиром на рисунке.

Электронейтральность полупроводника означает, что концентрация электронов в зоне проводимости равна концентрации дырок в валентной зоне. Из (П.10.5) и (П.10.7) находим

. (П.10.8)

Концентрация носителей тока увеличивается с ростом температуры и с уменьшением ширины запрещенной зоны.

Из с учетом (П.10.5) и (П.10.7) получаем

.

Выражаем химический потенциал

. (П.10.9)

При Т  0

.

Следовательно, уровень химического потенциала:

• расположен в середине запрещенной зоны при низкой температуре;

• чем выше температура, тем сильнее уровень приближается к той зоне, где масса частиц и плотность состояний меньше;

• расположен в середине запрещенной зоны при любой температуре при равенстве эффективных масс электронов и дырок.