Статистические распределения фермионов и бозонов

Идеальный газ фермионов или бозонов находится в фиксированном объеме, т. е. в потенциальной яме, при температуре Т. Частица в яме имеет дискретный энергетический спектр. Частицы газа обмениваются энергией и переходят между уровнями, число частиц в каждом энергетическом состоянии системы изменяется. Поэтому система описывается большим каноническим распределением. Откуда получаем среднее число частиц в одном состоянии на уровне энергии ε.

Фермионы имеют полуцелый спин и подчиняются принципу Паули – в одном квантовом состоянии не может быть более одной частицы. Среднее число частиц в одном состоянии описывается распределением Ферми–Дирака, которое получили Энрико Ферми в 1925 г. и Поль Дирак в 1926 г.

Бозоны обладают целочисленным спином, не имеют ограничения на число частиц в одном состоянии, и описываются распределением Бозе–Эйнштейна. Распределение для фотонов со спином получил Шатьендранат Бозе в 1924 г. Обобщение на случай частиц с произвольным целым спином дал Альберт Эйнштейн в 1924–1925 г.

Элементарные частицы фермионы и бозоны выполняют в природе разные функции. Фермионы в виде электронов, нуклонов, кварков образуют материю, из которой состоят тела. Бозоны в виде фотонов, фононов, глюонов, и-бозонов в виртуальном состоянии являются переносчиками взаимодействий между частицами материи. Составные частицы материи – атомы и молекулы могут быть фермионами или бозонами.

Большое каноническое распределение квантовой системы

Система в виде идеального газа при фиксированных T и V, обменивающаяся энергией и частицами с термостатом, описывается большим каноническим распределением. Оно дает число частиц на уровнях в многоуровневой системе.

Состояние i многоуровневой системы. Каждая частица ограниченной в пространстве стационарной квантовой системы имеет дискретный спектр энергии

.

Частное распределение частиц по уровням энергии образует состояние системы

,

где – число частиц на уровне. Полная энергия и число частиц в состоянииi

, . (4.1)

Вероятность состояния i. Используем большое каноническое распределение классической системы

.

Распределение у квантовой системы имеет аналогичный вид согласно принципу соответствия. Для вероятности дискретного состояния i получаем

, (4.2)

где – химический потенциал равновесной системы.Подставляем (4.1) в (4.2)

. (4.2а)

Распределения частиц по уровням энергии. Статистически независимые уровни энергии рассматриваем как подсистемы. По теореме умножения вероятностей независимых событий вероятность состояния системы равно произведению вероятностей состояний ее независимых подсистем

,

где – вероятность нахождениячастиц на уровнеk. Сравниваем с (4.2а) и получаем

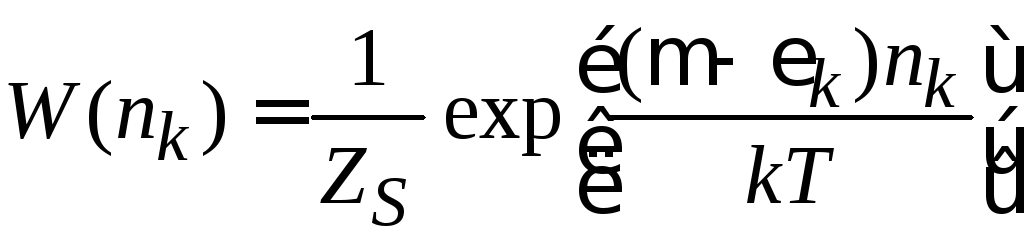, (4.3)

. (4.4)

Учтено, что для равновесной системы химический потенциал одинаков у всех подсистем.

Статистическая сумма подсистемы с энергией находится из нормировки вероятности

.

Подстановка (4.3) дает

. (4.5)

Для системы в макроскопическом объеме спектр энергии квазинепрерывный. В (4.3) и (4.5) заменяем

и получаем вероятность нахождения n частиц в состоянии с энергией и статистическую сумму

,

. (4.5а)

Среднее число частиц в состоянии с энергией без учета вырождения по спину, которое учитывается плотностью состояний, находим из определения среднего и (4.5а)

. (4.6)