Оператор проекции спина на произвольное направление

Получим оператор проекции спина на единичный вектор n, заданный в сферических координатах. Найдем собственные функции и собственные значения оператора .

Оператор проекции спина. Вектор n единичной длины, заданный на сфере Блоха углами , имеет декартовые проекции

, ,,

удовлетворяющие

.

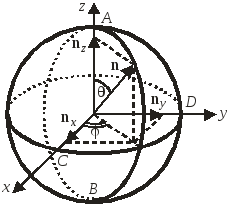
Сфера Блоха

Оператор спина проектируем на направление n

. (П.11.6а)

Подставляем

, ,,

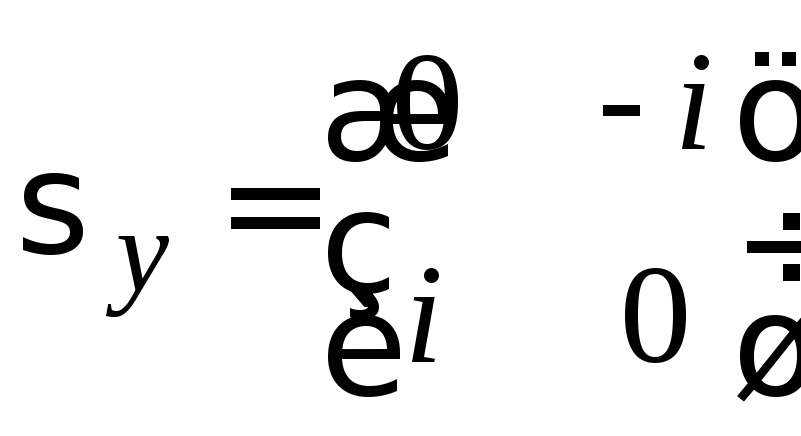и находим оператор проекции спина на направление, заданное углами θ и φ:

. (П.11.6)

С учетом (7.11) в виде

, ,,

из

получаем

. (П.11.6б)

Собственная функция

оператора удовлетворяет

, (П.11.6в)

где – собственное значение. Подстановкаииз (П.11.6) даетсистему однородных алгебраических уравнений

.

Ищем ,и.Условие совместности

дает

,

.

Проекция спина на любое направление . Этот парадоксальный результат следует из того, что соседние проекции отличаются на и не могут превышать, поскольку спин равен. В первое уравнение системы с собственным значением

подставляем

,

,

получаем

.

Находим решение

,

,

.

Нормировка

,

дает . Тогда с точностью до постоянной фазы собственная функция оператора проекции спина с собственным значениемравна

. (П.11.7)

Для перехода к собственному значению разворачиваем вектор, при этом

, .

Из (П.11.7) получаем

. (П.11.8)

Полученные состояния нормированы и ортогональны

,

.

Состояния инаходятся в противоположных точках сферы Блоха и образуют полный ортонормированный базис. Произвольное спиновое состояние разлагается по этому базису

.

Оператор проектирования спина. Для функций с собственными значениямис учетом (П.11.6а) и (П.11.6в)

,

выполняется

. (П.11.8а)

Определяем операторы проектирования спина на направления в виде

. (П.11.8б)

С учетом (П.11.8а) выполняется

, ,

, .

Для произвольной функции состояния спина

выполняется

,

,

, , (П.11.8в)

где Действие оператора проектирования физически реализует анализатор Штерна–Герлаха, показанный на рис. 1. Произвольное спинорное состояниепроектируется на направления. Вероятность соответствующего результата. После измерения состоянияпространственно разделены.

Частные случаи направлений. Оператор проекции спина (П.11.6)

для вектора n, направленного по оси z, когда ,, получает вид

.

Из (П.11.7) и (П.11.8)

, ,

находим собственные функции

,

,

совпадающие с (7.16).

Для вектора n, направленного по оси x, когда ,, дает

.

Из (П.11.7) и (П.11.8) находим

,

,

, .(П.11.9)

Для вектора n, направленного по оси y, когда ,, имеем

.

Из (П.11.7) и (П.11.8) получаем

,

,

, .(П.11.10)

Из (П.11.10) следует, что если в анализаторе Штерна–Герлаха с осью вдоль оси z выходящий пучок

направить в аналогичный анализатор с осью вдоль оси y, то из него вновь выйдут два пучка, идущие по разным направлениям.