Квантовая статистическая физика

Квантовая статистическая физика изучает системы из большого числа частиц, подчиняющихся законам квантовой механики:

электронный газ металла;

электроны и дырки в полупроводнике;

электромагнитное тепловое излучение в полости;

фононы в кристалле;

газ атомов при низкой температуре.

Учитываются квантовые свойства:

дискретность спектра энергии пространственно ограниченной

системы;

вырождение состояний по энергии благодаря спину;

тождественность микрочастиц;

принцип запрета Паули для фермионов.

Рассматриваются системы из множества частиц одинаковой природы, образующих идеальный газ и удовлетворяющих условиям:

объем газа гораздо больше объема частиц;

частицы двигаются независимо друг от друга;

частицы не взаимодействуют между собой на расстоянии.

Физические свойства многочастичной системы определяются ее энергетическим спектром и распределением частиц по уровням энергии. Рассмотрим по отдельности каждую из этих характеристик.

Энергетическая плотность состояний частицы

Энергетический спектр частицы зависит от гамильтониана и области пространства, доступной для частицы. Чем больше объем пространства, тем меньше расстояние между уровнями энергии. Для всех частиц рассматриваемого газа размеры доступного пространства одинаковые и спектры идентичные. При макроскопическом объеме газа спектр энергии частицы квазинепрерывный и характеризуется плотностью состояний – числом состояний в единичном интервале энергии

. (3.3)

Число состояний с энергией в интервале равно

. (3.3а)

Число частиц системы в интервале энергии равно произведению числа состоянийна среднее число частиц в одном состоянии

. (3.3б)

Получим плотность состояний частицы, используя объем фазового пространства, занятый состояниями, объем каждого состояния и вырождение состояний по энергии.

Кратность вырождения. Одним из квантовых чисел, определяющих состояние частицы, является спин S и его проекции числом . При отсутствии магнитного поля эти разные состояния имеют одинаковую энергию, тогда кратность вырождения

.

Для электрона и. Для фотонного газа, несмотря на спин. Теория относительности запрещает для фотона, движущегося со скоростью света, направление спина перпендикулярное к скорости, тогда остаются проекции по- и против скорости.

Плотность состояний. Условие квантования Бора–Зоммерфельда

означает, что бесспиновое состояние частицы с одной степенью свободы занимает фазовый объем, равный постоянной Планка h. Состояние частицы с f степенями свободы занимает объем . Безразмерный элемент фазового объема частицы

равен числу состояний частицы без учета ее спина. С учетом кратности вырождения находится число состояний

.

Из определения (3.3)

получаем плотность состояний частицы

, (3.4)

где – приращение объема фазового пространства при увеличении энергии на единицу. Состояния частицы с полной энергией ε находятся в фазовом пространстве размерностьюна замкнутой гиперповерхности. Она ограничивает объем

. (3.5)

При увеличении энергии объем возрастает и плотность состояний

. (3.5а)

При вычислении используется связь полной энергии частицы с импульсами и координатами– дисперсионное соотношение.

Плотность состояний свободной частицы f-мерного газа. Если нет внешних сил, действующих на частицу, то ее энергия не зависит от положения частицы в объеме газа. В (3.5а) интегрируем по координатам и получаем

,

где – объем импульсного пространства, ограниченный гиперповерхностью с энергией ε. Если энергия не зависит от направления импульса , то гиперповерхность является сферой. Объем шарового слоя находим из (П.2.2)

,

где dp и p – толщина и радиус слоя. В результате

. (3.5б)

В частности

;

;

. (3.5в)

Рассмотрим степенную зависимость полной энергии от модуля импульса

, (3.5г)

где s, t и u – вещественные числа; – кинетическая энергия. Из (3.5г) выражаем

, ,

.

Из (3.5б) получаем

. (3.5д)

Плотность состояний определяется кинетической энергией частицы.

Квадратичная зависимость энергии от импульса

, (3.6)

где ;– декартовы проекции импульса, соответствует,. Из (3.5д) получаем

. (3.7)

В частности:

,

где – скорость частицы;

;

. (3.7а)

В двухмерной системе плотность состояний не зависит от энергии, поэтому спектр частицы эквидистантный.

Плотность состояний нерелятивистской частицы f-мерного газа во внешнем поле . Безразмерный объем фазового пространства (3.5)

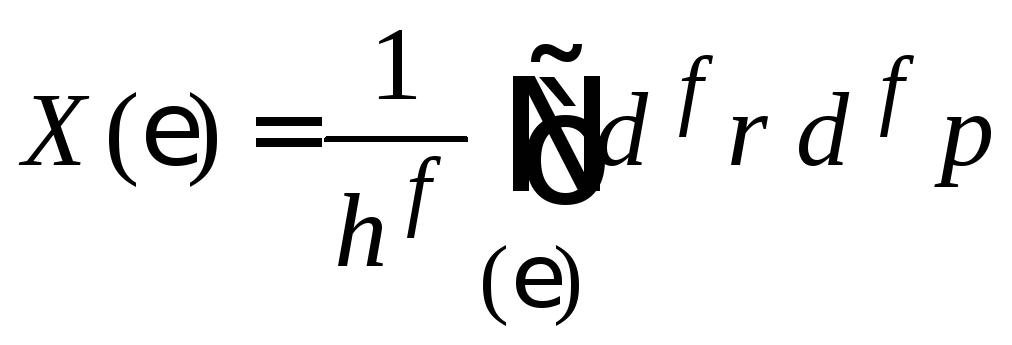
ограничен гиперповерхностью с энергией . При фиксированном ε и гиперповерхность в импульсном пространстве является сферой радиусом

.

Интегрирование по импульсам дает объем шара (П.2.1)

.

Результат интегрируем по координатам области, ограниченной поверхностью ,и получаем

,

.

Из (3.4)

находим плотность состояний

. (3.7б)

В частности:

;

. (3.7в)

Для двухмерного газа результат совпадает с (3.7а)

.