электричество и магнетизм

Сост:к.афизнд.вители

-мат.наук,доц.

В.Ф.Ким,

канд.физ.

-мат.наук,доц.

Э.А.Кошелев

Реце:ка.пенаук. зент,д.оц

Л.П.Панасенко

♥ Новосибирскийгосударстве

нный

техническийуниве

рситет, 2006

Прибмогутнормировыпоразнымвидпогрешнтьсям

остей.

Длятогочтзаранеебыоценивапогрешность,ковноситорую

данноесредствоизмеп )(иборконениячныйзул

ьтат,

пользуютсятакназываемыминормированнымизначениями

погрешности.Под

нормированнымизначениями

понимают

погрешности,являющиесяпредданельтипасредстваногоыми

измерения.

Обобщеннметролхарактогичеристикоййср дств

измеренияявляется

класст

очности,котоопрдопустимыеыйеделяет

пределывсехпогрешностей,атакжевседругиесвойства,влияющиена

точностьсредствизмерений.Чащесеговстречаютсятриклпассов

точности.

Классточностиприборазаданввидеотносительной

погрешности δ:

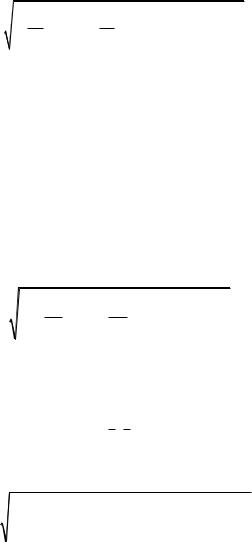
δ =

x

100% .

(1)

Тогпределопускаемойприбопогр(нойешности

x

максимальная

прибопогрнаяе

шность)равен

δx

x =

.

(2)

Данныйвидкласс

100

аточностиуказынаприборевнутриают

кружочка,н

апример1,5

γ =

x

100 %,

(3)

где xN – нормирующеезначение

xN

измеряемойвеличины

,которое

равнопределуизмерения

xmax дляприборов

снулевойотме

ткойна

краюшкалы

.Еслиженулеваяотметканахпосердится

едине шкалы,

тонормирующеезначение

xN

равнопротяженндиапазонасти

–30доА+60

измерений.На

приамперметра,для сошкалойот

величина xN = 60 − (−30)= 90А.

Пределдопускаемойприбопогрмаксимальнаянойешности(

приборнаяпог) ешность

авен

xN

.

(4).

x =

γ

Этот видклассаточнизонабражаютстиприборечислом

100

без

изображенкружочкаиподчеркивлия

ания,нап, ростоимер

1,5.

Наприборах

срезконеравномернойшкалой

классточности

указываетсядоляхотдлинышкалыобозначаетсячисломнад

уголком:

Классточностизаданввидепогрешности,

определяемойдвумячислами(

α/β)своеобразная( форма

относительпогрешной

ости):

δ

α

x

β1

max[%]

.

(5)

=

+

−

x

Тогпределопускаемойприбопогрмаксималнойешности(

ьная

приборнаяпогре

шность)равен

x

=

−α + β

)

x

β x

100.

(6)

{(

max }

Этотвидклассаочностиуказынаприборевидеаютдроби,

например0,02/0,01.

Предельприборныеинструментальные( )погрешности

x определяютлишьтакназываемыеоснповныегрешности.Вобщем

случаеинструментальныепогрешностизависяткакотизмеряемых

величинна(одномдиапазонеизмереприбодноийрагре

шность,

4

надругомдиапазонеизмеренияприбора

– другая),такиотусловий

проведенияизмеренийрабочие( усл заметновиягутл

ичатьсяот

нормальнвыходит,наприм,темперзапредатура

елы(20

± 5) оС,

относительнаявлажностьвнепредела30

–80ит.д.)В%.

ответственныхфизическэксперправильныйучхментах

инструментальныхпогр

ешноссоставляетейдельнзадачую

измерения.

Втаблпривкачествецеборовмаксимальприборной

погрешностиуказываюттодинизвидовпри ышеедпр нныхделов

допускаемойприбопог.рНнойешности

апример:

Максима

Наимено

Фабри

Тип

Класс

Предел

Цена

льная

прибора

ы

приборна

вание

чный

точнос

делен

№

или

измере

я

прибора

№

ти

ия

система

ния

погрешно

сть

1

Вольтмет

7388

Магнито

1,0

(0…

2В

2В

р

электрич

…В200)

еская

2

2Погрешность. косвенныхизмерений

Прикосвенномизмерениифизическойвеличиныеезн

ачение

вычисляетсяпоопред

еленнойформулечерезвеличины,получаемые

результатепр

ямыхизмерений.

f

Пустьнекотораяфизическаявеличина

являетсяфункцией

величин x, y,

z,... ,к оторыеопрпрямымиделяютсяизмерениями:

f = f (x, y, z, ...) .

(7)

Допустимтакже,что

x, y,

z,... распнормальномуределены

зазакону( Г

ау)ссореднеквадратотклоненСКО() ичнымиями

σ

x

, σ , σ , (обычнодляслучайныхпогрешнос

тейэтовыполняе

тся).

y z

f

Тогда,какдоказановте шибокр,

такжераспзакределенао

ону

ГауссаСКО,равным

5

G = (6,6726 ± 0,0008) 10−11Н м2 /

кг2 ,

(11)

т.е.используемоезначениевеличи

ны G содержит систематическую

погрешностьпорядка

σG = 3 10−14 Н м2 / кг2 .Этообстоятельс

твои

учитываетформула(10б).

3Представл. результатовизм ренийние

Результаизмеренийприводятсяыа

блицахизмерений

прямых

графиках.Втаблицыизмеренийзаписываютсярезультаты

измерений,атакжерезультаты

промежуточныхвычислений

.Длявсех

величинуказываюсоотверазмерносттс.Таблицаятвующие

измеренийвобязательномпорядкеимеетпоследний,итог

овый

столбец,гдеприв

одятсярезультатыизмеренийсучетом

погрешностей.Приэт мбл

юдаютсяправилаокругления

результатовизмерений.

Окончательнизмеренийрезультаприводятсяакжеы

выводахполабораторнойработесуказаниемпогрешностиизмерений.

Припредставлрезультатовизмеренийследуетнии

руководствоватьсяследующимиправиламиокруглениячисловых

значенийфиз

ическихвеличин.

1. Погрешность результатаизмеок енияуглется

доодной

значащейцифры,еслиперваязначащцифрапог яавнаешности3

более.

2. Погрешность результатаизмеок енияуглется

додвух

значащихцифр,еслипе

рваязначащцифрапогрешностия

1или2.

3. Среднеезначение

результатаизмеок енияуглется

дотого

жед сятичногоразряда

,которымоканчиваетсяокругленноезнач

ение

погрешности.

вокончательномответе

(впо -

4. Округпроизводитсялишьение

следнем,итогстовомлбце

таблицизмер),всепредварителний

ьные

вычипрсодлеводятнойия

-двумязапаснымизначащимици

фрами.

7

Результатизмерения

однойитойжефизическойвеличины

может бытьпредстаразличномнв видезависимостиотзначения

погрешностиизм

ерений:

x = (3,6 ± 0,3),

x = (3,57 ± 0,06),

x = (3,574 ± 0,013) .

Впервивтзаписяхоройрезультатаизмерений

последняяцифра

всреднем значенииф

изическойвеличины(«6»первойзаписи, «7»

–

вовторойзаписи)оказывается

сомнительной,аостальнцифрые

являются достоверными.Втретьейзаписирезультатаизмерений

сомнительнымиявляютсяуже

двецифры

всреднемзначении

физическойвел

ичины(«7»«4»

).

4Установление. зависимостейфизичвеличинских

Когдауст зависимостьнавливаетсяоднойвеличиныотдругой

сравниваетсяте

оретическиожидаемойзависимостью,тообычной

являетсяпрактикапостролинзавейныхяи.Однасимостейиз

причинприменения

этогопралежитвнашемилавосприятии:

различитьдвеблизпофокриелиниимевесьмаыенепросто,

прямаялиниялегкоузна« »средидртся

угихлиний.

Рассмслучай,котримгда

погрешностьимееттольковеличина

y.

Напра ктикеэтотслучайвстречаетсядово

льночасто.Б леебщий

случайтребуетусложненияпробрцедурыданных.ботки

Пустьтеоретичемодельпредлинейнуюскаязывает

зависимость.Задача

остоитвтом,чтобычерез«»экспериментальные

точкипровести

наилучшимобразо

прямуюлиниюсравнить

теоретическиожидаемойзависимостью.

Пуиснаилучшаякомаятьпримеетвид

y = ax + b,

(12)

гдеуглкоэффициентвойтан(угнаклоналаенс)

a

ивеличина

смещения

b

подлежатопределениюснекоторыми

среднеквадратичнымипогрешност

ями σa и σb .

Методнаименьшихквадратов

– одинизстандартныхметодов

матемастатистикииче.Вэтомметоденаилукой

чшиезначения

параметровпрямой

a и b находятизусловминияуммыя ума

квадратоввеличино

тклонений d

i

= y − (ax+ b) :

i

i

8

k =

∑ xi yi

,

σk =

∑( yi

− axi )2

.

(20)

∑ xi2

(n −1)xi2

Приведеннформулые

нетребуютсобственнопостроения

графика.Онидаютстрогийаналитическийспособстатистической

обработкиэкспериме нтальда.нных

Существует

упрощенныйспособ

оценкипараметровнаилу

чшей

прямойподанным,предстнагра,которыйвленнымфикеработаеттем

лучше,чембольшеимеетсяэкспериментальныхточекнаграфике

(б олее15

–20точек).

Дляопределпогрешностейния

σa ,

σb и σk

поступим

следующимобр

азом.Рабочий«уча» абсцисток

сучасток(,на

которомрасположеныэкспериментальныеточки)разбиваемнатри

равныеча

стивдальнейшембудемобр

ащатьвниманиена

среднюю еечасть.

Поворачиваем наилучшуюпрямуюлинивокругцентра

яжести

(x, y) такимобразом,чт

обыналевомучасткевышпр

ямойоказалось

вдвоебольшеэксп точекриме,чемподней,аправомтальных

участке – наоборот.Затемповорлиниюачиваемямуютаким

образом,чтобыналевомучасткенижепрямойоказалосьвдвоебольше

экспериментальныхточек,

чемнадней,направомучастке

–

наоборот.Обозначимразницувуглк эффициентахвыхчерез

a .

Тогда

σa =

a /

n .

(21)

Теперь смещаем наилучшуюпрямуювниз

параллельнос

амойсебе

такимобразом,чтонаднейбывдвоелобточекльше,чемподней.

Затемсмещапрямуюввпараерх

ллельносамойсебетакимобразом,

чтоподнейбывдвоелобточекльше,чемнадней.Обозначим

b .Т огда

разницуввелисмещениячеринез

σb =

b /

n .

(22)

Есогласнолитеоретическоймоделиожидаемаяпрямая

оходит

черезначалокоординатто(19),рабочий«уча» абсциссток

разбиваемтакженаравныеича

стивдальнейшембудем

обращатьвниманиенапервую

– левую,ближнююкначалукоорд

инат,

еечасть.

10