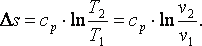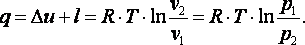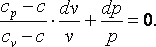Политропный процесс

Политропный процесс

Материал из Википедии — свободной энциклопедии

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс () и адиабатный процесс ().

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны  и ( и не меняются при изменении термодинамических параметров).

Показатель политропы[править | править исходный текст]

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь  — теплоёмкость газа в данном процессе,  и  — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: 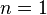, так как , значит, по закону Бойля — Мариотта 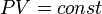, и уравнение политропы вынуждено выглядеть так: .

• Изобарный процесс: 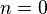, так как 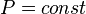, и уравнение политропы вынуждено выглядеть так: .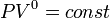

• Адиабатный процесс:  (здесь 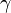 — показатель адиабаты), это следует из уравнения Пуассона.

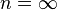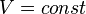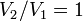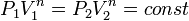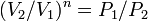• Изохорный процесс: , так как , и в процессе , а из уравнения политропы следует, что , то есть, что , то есть 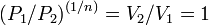, а это возможно, только если 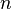 является бесконечным.

Различные значения показателя политропы
Значение показателя политропы	Уравнение	Описание процесса
	—	Хотя этот случай не имеет практического значения для наиболее распространённых технических приложений, показатель политропы может принимать отрицательные значения в некоторых специальных случаях, рассматриваемых, например, в некоторых состояниях плазмы в астрофизике.[1]
		Это изобарный процесс (протекающий при постоянном давлении)
		Это изотермический процесс (протекающий при постоянной температуре)
	—	Это квазиадиабатические процессы, протекающие, например, в двигателях внутреннего сгорания во время расширения газа
	—	—- это показатель адиабаты, используемый при описании адиабатического процесса (происходит без теплообмена газа с окружающей средой)
	—	Это изохорный процесс (протекающий при постоянном объёме)

Когда показатель n лежит в пределах между любыми двумя значениями из указанных выше (0, 1, γ, или ∞), то это означает, что график политропного процесса заключён между графиками соответствующих двух процессов.

Заметим, что , так как .

Термодинамические процессы: изохорный, изобарный, изотермический, адиабатный, политропный

4.2.1.Изохорный процесс (v=const)

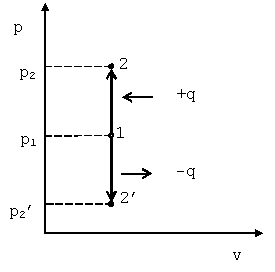
Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис. 4.1) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа (см. &1.6) при v=const. В pv-координатах график процесса представляет собой прямую линию, параллельную оси p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).

Рис. 4.1. График изохорного процесса в p-v координатах

Запишем для точек 1 и 2 уравнения состояния:p₁·v=R·T₁; p₂·v=R·T₂. Следовательно, для изохорного процесса

(4.6)

Приращение внутренней энергии газа

(4.7)

Работа газа

так как dv=0.

Энтальпия газа i_v=u+p·v, а di_v=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому

(4.8)

Энтропия 

То есть

(4.9)

4.2.2.Изобарный процесс (p=const)

В p-v координатах график процесса представляет собой прямую линию параллельную оси v (рис. 4.2). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния:p·v₁=R·T₁; p·v₂=R·T₂.

Рис. 4.2. График изобарного процессав p-v координатах

Следовательно, для изобарного процесса

(4.10)

Приращение внутренней энергии газа Работа газа  Так как p·v₂=R·T₂, аp·v₁=R·T₁, то l=R·(T₂-T₁). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус. Из выражения (4.3) следует, что в изобарном процессе q=c_p·(T₂-T₁). В соответствии с первым законом термодинамики для изобарного процесса можно записать dq=du+p·dv= du+d(p·v)=di. Поэтому в изобарном процессеdi=q=c_p·(T₂-T₁). Из соотношений, характеризующих изобарный процесс, вытекает известное уравнение Майера. Так как dq=c_p·dT=c_v·dT+dl=c_v·dT+R·dT, тоR=c_p-c_v.

Используя выражение (4.5), можно показать, что в изобарном процессе энтропия газа

(4.11)

4.2.3.Изотермический процесс (T=const)

В p-v координатах график процесса изображается равнобокой гиперболой (рис. 4.3). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Рис. 4.3. График изотермического процесса вp-v координатах

Запишем для точек 1 и 2 уравнения состоянияp₁·v₁=R·T; p₂·v₂=R·T. Следовательно, для изотермического процесса p₁·v₁=p₂·v₂=const.

Приращение внутренней энергии газа

Работа газа

(4.12)

Теплота, подводимая в процессе

(4.13)

Изменение энтальпии газа Δi=Δu+Δ(p·v)=0.

Изменение энтропии газа

(4.14)

4.2.4.Адиабатный процесс

Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.

В соответствии с первым законом термодинамики dq=c_v·dT+p·dv=c·dT, где с – теплоёмкость термодинамического процесса. Тогда можно записать, что

(4.15)

Продифференцируем уравнение состояния идеального газа и запишем

(4.16)

Так как R=c_p-c_v, то выражение (4.15) можно переписать с учётом (4.16) следующим образом:

(4.17)

Выполним преобразования выражения (4.17).

(4.18)

Разделим выражение (4.18) на (c_v-c)·p·v и получим:

(4.19)

Обозначим , тогда

Следовательно

(4.20)

В адиабатном процессе dq=0, то есть c·dT=0. Поэтому c=0. Значит в адиабатном процессе 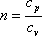. Эту величину принято обозначать буквой  и называть показателем адиабаты.

Поэтому в p-v координатах адиабатный процесс изображается неравнобокой гиперболой v^k·p=const (рис. 4.4). Так как k>1, то адиабата проходит круче гиперболы. Адиабатный процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Рис. 4.4. График адиабатного процесса в p-v координатах

Запишем для точек 1 и 2 уравнения состоянияp₁·v₁=R·T₁; p₂·v₂=R·T₂. Так как в адиабатном процессе p₁·v₁^k=p₂·v₂^k, то , , .

Приращение внутренней энергии газа .

Так как , а , то , а . Поэтому

(4.21)

Работа газа в адиабатном процессе выполняется за счёт его внутренней энергии. Так как в адиабатном процессе отсутствует обмен теплотой с окружающей средой, то в соответствии с первым законом термодинамики имеем l+Δu=0 или l=-Δu. Поэтому

(4.22)

Изменение энтальпии газа в адиабатном процессе может быть определено исходя из следующих соображений:

Так как , то в итоге получим

(4.23)

Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-sкоординатах адиабатный процесс изображается прямой линией, параллельной оси температур.

4.2.5. Политропный процесс

Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости с_п.

В политропном процессе dq=c_п·dT.

Для получения графика политропного процесса в p-v координатах будем придерживаться тех же рассуждений, что и при получении графика адиабатного процесса. Заменим в соотношениях, полученных при изучении адиабатного процесса, обозначение теплоёмкости с на с_п и обнаружим, что p·vⁿ=const, а . В дальнейшем всё, что написано об адиабатном процессе, можно распространить на описание политропного процесса, заменяя в выражениях k на n.

Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.

Так как , то можно записать

                  ;     ;     ;     .

Из последнего выражения видно, что при n>k c_п>0, а при k>n>1 c_п<0.

В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.

При n=k имеем адиабатный процесс.

При n=0 имеем р₁·v₁⁰=р₂·v₂⁰, то есть изобарный процесс (p₁=p₂).

При n=1 имеем р₁·v₁= р₂·v₂, то есть изотермический процесс.

При n=∞ имеем  или , что равносильно  или , то есть изохорный процесс.