
Математическая логика
.docx 1.
A → B ⊢ (C & A) → (C & B)
1.
A → B ⊢ (C & A) → (C & B)
a) Проверка выводимости методом Куайна:
По теореме дедукции, перенесём посылку в правую часть и проверим выводимость формулы:
(A→ B)→ ((C & A) → (C & B))
Подставляя С = 0, получаем:
(A → B) → ((0 & A) → (0 & B)) = (A → B) → (0 → 0) = (A → B) → 1 = 1
при любой интерпретации A и B.
Подставляя С = 1, получаем:
(A → B) → ((1 & A) → (1 & B)) = (A → B) → (A → B) = 1
при любой интерпретации A и B.
Получили, что формула (A → B) → ((C & A) → (C & B))
является тавтологией, а значит, выводима в исчислении высказываний.
б)Проверка выводимости методом редукции:
По теореме дедукции, перенесём посылку в правую часть и проверим выводимость формулы:
(A → B) → ((C & A) → (C & B))
Пусть в некоторой интерпретации наша формула имеет значение 0.
Тогда, по свойству импликации
(A → B) = 1, (C & A) → (C & B) = 0.
(A
→ B) =
![]() A
∨ B = 1,
A
∨ B = 1,
значит в этой интрепретации A = 0, B =1. Но тогда:
(C & 0) → (C & 1) = 0 → C = 1
Противорчие.
в) Проверка выводимости методом резолюции:
Преобразуем в конъюнкцию предложений отдельно гипотезу и отрицание целевой функции.
A
→ B = ![]() A
∨ B
A
∨ B
![]() ((C
& A) → (C & B)) =
((C
& A) → (C & B)) =
![]() (
(![]() (C
& A) ∨ (C & B)) = (C & A) & (
(C
& A) ∨ (C & B)) = (C & A) & (![]() C
∨
C
∨![]() B)
B)
Резольвируем предложения:
1.![]() A
∨ B
A
∨ B
2. C
3. A
4.
![]() C
∨
C
∨
![]() B
B
5. B - по правилу резолюции из 1. и 3.
6.
![]() B
- по правилу резолюции из 2. и 4.
B
- по правилу резолюции из 2. и 4.
7. из 5. и 6. получаем пустую формулу
Получена пустая формула, выводимость доказана.
2.

3.
![]()
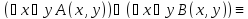

![]()


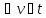
![]()


 (
(![]()


 (
(![]()

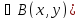
4. Опишем сначала идею. Данные имеют вид 11111 0 11 0 111.
Сначала занулим первый и последний символ данных: 01111 0 11 0 110
Далее будем “сдвигать” эти нули к центру, пока один из них не совпадет с первоначальным нулем.
10111 0 11 0 101
11011 0 11 0 011
11101 0 11 0 111
Тогда второй ноль укажет позицию, до которой надо сдвинуть первоначальные нули, чтобы получить требуемый результат:
111010110111
|/ / - сдвиг
111011011111 - требуемый результат.
Программа:
//ставим 0 в начале и в конце
q0
1
 0
R q1
0
R q1
q1
1
 1
R q2
1
R q2
q1
0
 0
R q3
0
R q3
q2
1
 1
R q2
1
R q2
q2
0
 0
R q3
0
R q3
q3
1
 1
R q3
1
R q3
q3
0
 0
R q4
0
R q4
q4
1
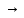 1
R q4
1
R q4
q4
0
 0
L q5
0
L q5
//циклически двигаем нули-метки к центру
q5
1
 0
L q6
0
L q6
q6
1
 1
L q36
1
L q36
q6
0
 0
L q7
0
L q7
q36
0
 0
L q7
0
L q7
q7
1
 1
L q7
1
L q7
q7
0
 0
L q8
0
L q8
q8
1
 1
L q8
1
L q8
q8
0
 1
R q9
1
R q9
q9
1
 0
R q10
0
R q10
q10
1
 1
R q11
1
R q11
q11
1
 1
R q11
1
R q11
q11
0
 0
R q12
0
R q12
q12
1
 1
R q12
1
R q12
q12
0
 0
R q13
0
R q13
q13
1
 1
R q13
1
R q13
q13
0
 1
L q5
1
L q5
//если правый нолик-метка дошел до нолика, двигаем центровые нолики влево
q5
0
 1
L q14
1
L q14
q14
1
 0
L q15
0
L q15
q15
1
 1
L q15
1
L q15
q16
1
 0
R q17
0
R q17
q17
1
 1
R q17
1
R q17
q17
0
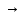 1
L q14
1
L q14
q16
0
 конец
конец
//если левый нолик-метка дошел до нолика, двигаем правый нолик метку на одну позицию влево, потом сдвигаем центровые нолики вправо
q9
0
 0
R q18
0
R q18
q18
1
 1
R q18
1
R q18
q18
0
 0
R q19
0
R q19
q19
0
 1,
конец
1,
конец
q19
1
 1
R q20
1
R q20
q20
1
 1
R q20
1
R q20
q20
0
 1
L q21
1
L q21
q21
1
 0
L q22
0
L q22
q23
1
 1
L q23
1
L q23
q23
0
 0
L q24
0
L q24
q24
1
 1
L q24
1
L q24
q24
0
 1
R q25
1
R q25
q25
1
 0
R q26
0
R q26
q26
1
 1
R q26
1
R q26
q26
0
 1
R q27
1
R q27
q27
1
 0
L q23
0
L q23
q27
1
 конец
конец
Проверим машину на данных 10101, те x=y=z=1.
Указан вид ленты, когда машина переходит в соответствующее состояние.
q0 10101
q1 00101
q2 00101
q3 00101
q4 00101
q5 00101
q6 00100
q7 00100
q8 00100
q9 10100
q18 10100
q19 10100
10101, конец
