6. Графики распределения концентрации примеси для трех временных значений - случай, когда доза постоянна и не связана с диф. Длинной

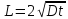
Для дискретного источника примеси:

L=0,1мкм; 0,5 мкм; 1 мкм

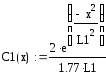
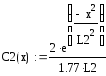
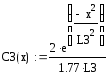
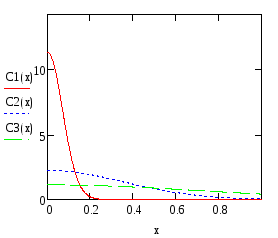
С_i = C/Q

Распределение легирующей примеси

Распределение легирующей примеси с логарифмической шкалой:

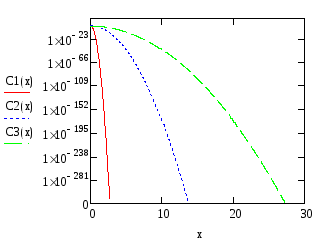
Из графиков видно, что с увеличением времени легирующая примесь расплывается в веществе, стараясь принять более равномерное распределение и соответственно чем дальше примесь уходит в глубь вещества, тем меньше становится поверхностная концентрация на границе вещества.

Распределение при бесконечном источнике примеси (С_s –const, распределение по erfc):

Аналогично графикам распределения примеси по Гауссу, показано распределение по erfc для тех же временных значений:

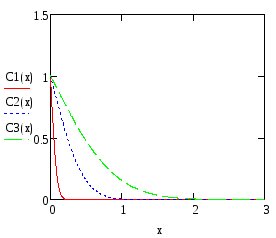
Распределение легирующей примеси при бесконечном источнике:

Распределение легирующей примеси при бесконечном источнике с логарифмической шкалой:

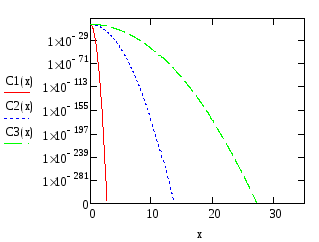
Из графиков видно с увеличением времени увеличивается глубина внедрения примеси, а также её доза. Так как в данном случае источник примеси бесконечный примесь внедряется с максимальной скоростью, а поверхностная концентрация С_s является постоянной.

7. РЕШЕНИЕ ЗАДАЧ:

а) Вычислить время процесса для диффузии бора с постоянной дозой в n-кремниевой подложке при следующих условиях:

Решение

Доза постоянна.

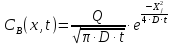- функция Гаусса

Величина поверхностной концентрации есть функция от времени:

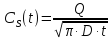
Параметры коэффициента диффузии бора в кремнии (справочные данные):

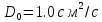
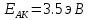
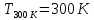
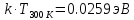
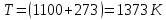
Дано:

Т=1100С

Cs=4*10¹⁷ см^-3

Xj=3мкм

Св=10^-15см^-3

t=?

Коэффициент диффузии при Т :

см²/с

Время диффузии из функции Гаусса:

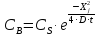
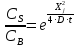
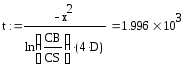с

Ответ: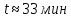

б) Вычислить время процесса для диффузии бора с постоянной поверхностной концентрацией в n-кремниевой подложке при следующих условиях:

Решение

Внедренная доза (из предыдущей задачи)

см^-2

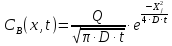- функция Гаусса

Величина поверхностной концентрации есть функция от времени:

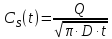
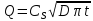
Время:

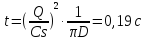
Дано:

Т=950С

Cs=2,5*10²⁰ см^-3

внедренная доза –

из предыдущей задачи

B Si

Сs=const

t=?

Ответ: t=0,19c