
- •Специальные главы физики
- •Группа рн
- •Статистическая физика Основные положения
- •Основы теории вероятностей Вероятность случайного события
- •Характеристики случайной дискретной величины Среднее значение величины
- •Свойства среднего
- •Относительная флуктуация
- •Характеристики случайНой непрерывНой величиНы
- •Биномиальное распределение
- •Условие нормировки
- •Распределение Пуассона
- •Производящая функция
- •Средние значения и дисперсия
- •Примеры
Средние значения и дисперсия
 ,
,
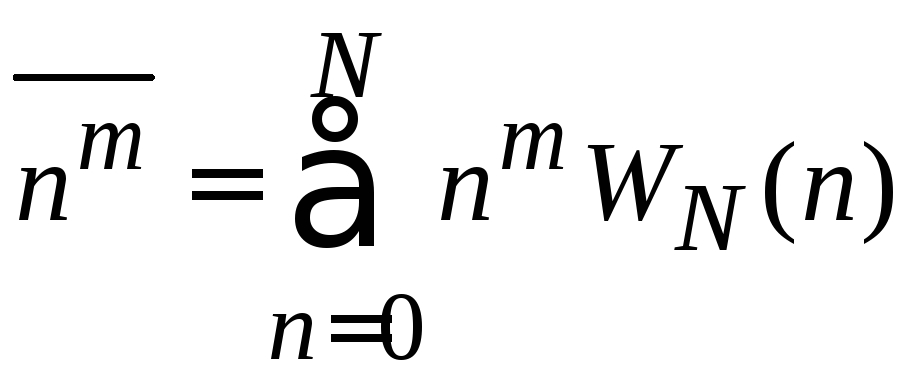 ,
,
![]() .
.
Из (1.22) находим
 ,
(1.24)
,
(1.24)
 ,
,
 ,
(1.25)
,
(1.25)
 .
(1.26)
.
(1.26)
Примеры
Для распределения Пуассона найти производящую функцию и
 .
.
Используем производящую функцию (П.1.5) для биномиального распределения и (П.1.6)
![]() ,
,
![]() ,
,
тогда
![]() .
.
Учитывая
![]() и
и
![]() ,
,
где
![]() ,
получаемпроизводящую
функцию распределения Пуассона
,
получаемпроизводящую
функцию распределения Пуассона
![]() .
(П.1.14)
.
(П.1.14)
Из (П.1.14) и (1.25)
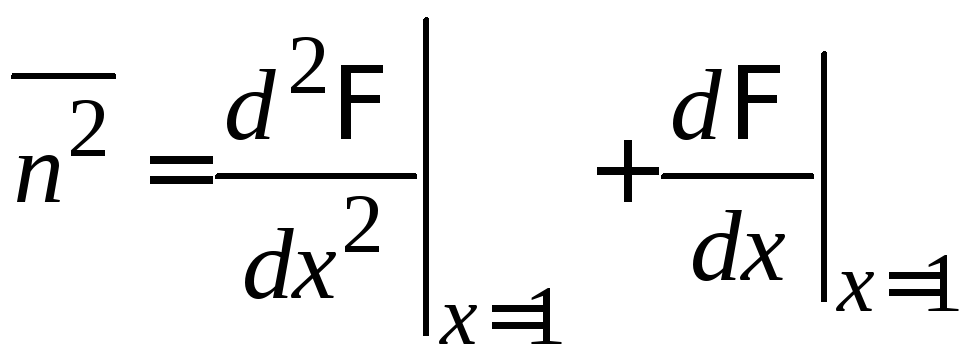
с учетом
![]() ,
,
 ,
,
следует (1.20)
![]() .
.
Найти распределение времен свободного пробега электрона металла.
Согласно классической теории в узлах кристаллической решетки металла находятся ионы, валентные электроны образуют идеальный газ. Любой макроскопический объем металла электрически нейтрален, поэтому на электрон не действуют электростатические силы и благодаря тепловому движению он свободно перемещается от одного столкновения с ионом до следующего.
Вероятность
столкновения
электрона
за единицу времени
а
не зависит
от t
при термодинамическом равновесии.
Вероятность столкновения за время dt
равна
![]() .
.
Функция распределения времен свободного пробега w(t) равна вероятности того, что время свободного движения лежит в единичном интервале около значения t.
Вероятность
двух независимых событий – свободного
движения электрона до момента t
и столкновения в следующий промежуток
dt
– согласно теореме о независимых
событиях равна
![]() и является
уменьшением вероятности обнаружения
электрона при переходе от t
к
и является
уменьшением вероятности обнаружения
электрона при переходе от t
к
![]() ,
т. е. равна
,
т. е. равна![]() .
В результате
.
В результате
![]() .
.
Разделяя переменные и интегрируя, получаем,
![]() ,
,
![]() .
.
Из условия нормировки

находим
![]() .Среднее
время свободного пробега
.Среднее
время свободного пробега
 (П.1.22)
(П.1.22)
обратно вероятности столкновения за единицу времени. Функция распределения времен свободного пробега равна
![]() (П.1.23)
(П.1.23)
– вероятность свободного движения в течение времени t уменьшается экспоненциально с ростом t.
Найти скорость дрейфа
 электронов металла в электрическом
полеЕ.
электронов металла в электрическом
полеЕ.
За
время свободного пробега t
электрон набирает скорость
![]() ,
где ускорение
,
где ускорение![]() .
Если при столкновении упорядоченная
скорость теряется, то средняя скорость
.
Если при столкновении упорядоченная
скорость теряется, то средняя скорость
![]() .
.
Время
свободного пробега меняется от
столкновения к столкновению. Пусть
электрон испытывает последовательно
N
столкновений с временами свободного
пробега t1,
t2,…,
tN
и средними скоростями
![]() ,
тогда скорость дрейфа
,
тогда скорость дрейфа
 .
.
Поделив
числитель и знаменатель на N,
и полагая
![]() ,
получаем
,
получаем
 .
.
Используя распределение (П.1.23), находим
![]() ,
,
 .
.
В результате скорость дрейфа
![]() (П.1.24)
(П.1.24)
пропорциональна электрическому полю и среднему времени свободного пробега электрона, где подвижность электронов
![]() .
.
